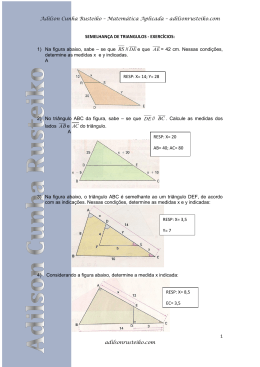
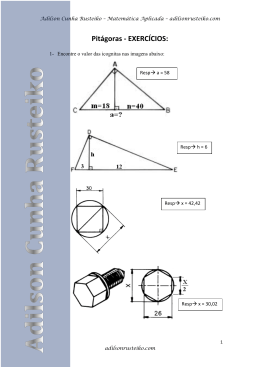
Adilson Cunha Rusteiko – Matemática Aplicada – adilsonrusteiko.com
Lei dos Senos e Cossenos - EXERCÍCIOS:
Adilson Cunha Rusteiko
1)
Determine a altura de um morro em relação a uma região plana que
existe em volta. Para isso, foi preciso fazer duas medições com o
teodolito. Inicialmente, o teodolito foi colocado em um ponto A.
Mirando o ponto V, o mais alto do morro, verificamos que o ângulo
dessa linha visual com o horizontal era de 10°. Em seguida, o
topógrafo aproximou-se do morro e fixou o teodolito no ponto B.
Nessa posição, mirando o ponto V, o mais alto do morro, ele verificou
que o ângulo da linha visual com o horizonte passou a ser de 26°.
Sabendo que a distância AB era de 100 m, qual é a altura do morro?
Resp.: 27,62 m
2) Em uma região há um rio com curso irregular. Sua largura não é
constante e ele faz muitas curvas. Entre os pontos A e B, situados em
margens opostas, deseja-se construir uma ponte. Para isso, é
necessário determinar a distância AB. O topógrafo, que esta na
margem inferior do desenho que vemos abaixo, assinala com uma
estaca um ponto C qualquer. Com a trena ele mediu a distancia AC e
encontra 56m. Com o teodolito ele mediu os ângulos BÂC e ACB
encontrando 118° e 35°, respectivamente. Qual será a distancia AB.
Resp.: 70,75 m
1
adilsonrusteiko.com
Adilson Cunha Rusteiko – Matemática Aplicada – adilsonrusteiko.com
Adilson Cunha Rusteiko
3) O topógrafo utilizou o mesmo método descrito no exercício 2 para
calcular a altura de uma torre que se encontra do outro lado de um
rio. Calcule sua altura, utilizando os dados que estão na figura abaixo.
Resp.: 95,7 m
4) Entre os pontos A e B, situados em uma fazenda, existe um morro. O
teodolito colocado no ponto C consegue mirar tanto A quanto B.
Sabendo que CA = 76 m, CB = 90 m e ACB = 126°, calcule a distância AB
Resp.: 148 m
5) Achar C, c e d, através da lei dos senos, sendo B = 25°, D = 80° e b =
381 mm.
Resp.: C= 75°
d = 887,83 mm
c = 870,8 mm
6) Achar B, b e d, através da lei dos senos, sendo C = 25°, D = 72° e c =
213,36 mm.
Resp.: b = 501,09 mm
B = 83°
d = 480,14 mm
7) Achar D, d e b, através da lei dos senos, sendo C = 47° 30’, B = 53° 18’
e c = 127 mm.
Resp.: D= 79° 30’
d = 169,37 mm
b = 137,57 mm
2
adilsonrusteiko.com
Adilson Cunha Rusteiko – Matemática Aplicada – adilsonrusteiko.com
8) Achar C, c e b, através da lei dos senos, sendo D = 20°20’, B = 40° e d =
508 mm.
Adilson Cunha Rusteiko
Resp.: C= 119° 40’
b = 939,72 mm
c = 1.270,32 mm
9) (UF-RJ) O polígono regular representado
na figura tem lado de medida igual a 1 cm
a o ângulo α mede 120°. Determine o raio
da circunferência circunscrita.
Resp.: 1,22 cm
10) (UF – MG) Na figura, B é o ponto médio do segmento DE a ABCD é um
retângulo de lado DC = 1 e DA = 2. Determine AE.
Resp.: AE = 2,83
cm
3
adilsonrusteiko.com