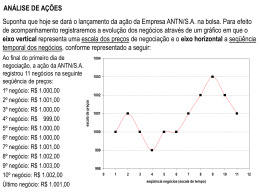
Equilíbrio de Corpos Extensos
1. (G1 - ifsp 2013) Em um parque de diversão, Carlos e Isabela brincam em uma gangorra que
dispõe de dois lugares possíveis de se sentar nas suas extremidades. As distâncias relativas
ao ponto de apoio (eixo) estão representadas conforme a figura a seguir.
Sabendo-se que Carlos tem 70 kg de massa e que a barra deve permanecer em equilíbrio
horizontal, assinale a alternativa correta que indica respectivamente o tipo de alavanca da
gangorra e a massa de Isabela comparada com a de Carlos.
a) Interfixa e maior que 70 kg.
b) Inter-resistente e menor que 70 kg.
c) Interpotente e igual a 70 kg.
d) Inter-resistente e igual a 70 kg.
e) Interfixa e menor que 70 kg.
2. (Uerj 2013) Um homem de massa igual a 80 kg está em repouso e em equilíbrio sobre uma
prancha rígida de 2,0 m de comprimento, cuja massa é muito menor que a do homem.
A prancha está posicionada horizontalmente sobre dois apoios, A e B, em suas extremidades,
e o homem está a 0,2 m da extremidade apoiada em A.
A intensidade da força, em newtons, que a prancha exerce sobre o apoio A equivale a:
a) 200
b) 360
c) 400
d) 720
www.nsaulasparticulares.com.br
Página 1 de 10
3. (Ufrgs 2013) Nas figuras (X) e (Y) abaixo, está representado um limpador de janelas
trabalhando em um andaime suspenso pelos cabos 1 e 2, em dois instantes de tempo.
Durante o intervalo de tempo limitado pelas figuras, você observa que o trabalhador caminha
sobre o andaime indo do lado esquerdo, figura (X), para o lado direito, figura (Y).
Assinale a alternativa que preenche corretamente as lacunas da sentença abaixo, na ordem
em que aparecem.
Após o trabalhador ter-se movido para a direita (figura (Y)), podemos afirmar corretamente que,
em relação à situação inicial (figura (X)), a soma das tensões nos cabos 1 e 2 __________,
visto que __________.
a) permanece a mesma - as tensões nos cabos 1 e 2 permanecem as mesmas
b) permanece a mesma - a diminuição da tensão no cabo 1 corresponde a igual aumento na
tensão no cabo 2
c) aumenta - aumenta a tensão no cabo 2 e permanece a mesma tensão no cabo 1
d) aumenta - aumenta a tensão no cabo 1 e permanece a mesma tensão no cabo 2
e) diminui - diminui a tensão no cabo 1 e permanece a mesma tensão no cabo 2
4. (Espcex (Aman) 2013) Uma barra homogênea de peso igual a 50 N está em repouso na
horizontal. Ela está apoiada em seus extremos nos pontos A e B, que estão distanciados de
2 m. Uma esfera Q de peso 80 N é colocada sobre a barra, a uma distância de 40 cm do
ponto A, conforme representado no desenho abaixo:
A intensidade da força de reação do apoio sobre a barra no ponto B é de
a) 32 N
b) 41 N
c) 75 N
d) 82 N
e) 130 N
www.nsaulasparticulares.com.br
Página 2 de 10
5. (Upf 2012) Uma barra homogênea de 30 kg de massa e 6 m de comprimento é apoiada em
C e em D, como na figura. Sendo que o apoio C tem força de reação que vale 120 N, a
distância X necessária para que a barra se mantenha em equilíbrio é, em m, de:
2
(considere g = 10 m/s )
a) 1
b) 1,5
c) 2
d) 2,5
e) 0,5
6. (G1 - ifsp 2012) O quadrinho mostra o Garfield tentando pescar o filé de seu dono com uma
vara cuja força peso, de módulo 20 N, está representada em seu centro de gravidade, CG.
Para conseguir seu almoço, o gato utilizou um fio de nylon de massa desprezível com um anzol
e um conjunto de chumbinhos, totalizando 0,4 N de peso, pendurados na ponta.
Considerando-se as distâncias indicadas na figura, numa situação em que a vara esteja em
equilíbrio, sendo segurada pelas duas patas de Garfield, a intensidade da força F, em newtons,
aplicada pela pata esquerda do gato na vara, é igual a
a) 75.
b) 65.
c) 55.
d) 45.
e) 35.
7. (Acafe 2012) Um instrumento utilizado com frequência no ambiente ambulatorial é uma
pinça. Considere a situação em que se aplica simultaneamente uma força F de módulo 10 N
como se indica na figura a seguir.
O módulo da força, em newtons, que cada braço exerce sobre o objeto colocado entre eles é:
a) 15
b) 8
c) 10
d) 4
www.nsaulasparticulares.com.br
Página 3 de 10
8. (G1 - cps 2012) Você já deve ter visto em seu bairro pessoas que vieram diretamente da
roça e, munidas de carrinhos de mão e uma simples balança, vendem mandiocas de casa em
casa.
A balança mais usada nessas situações é a apresentada na figura a seguir.
(Considere desprezíveis a massa do prato com seus cordames e a massa da haste por onde
corre o massor.)
A balança representada está em equilíbrio, pois o produto da massa do massor pela distância
que o separa do ponto P é igual ao produto da massa que se deseja medir pela distância que
separa o ponto em que os cordames do prato são amarrados na haste até o ponto P.
Considere que no prato dessa balança haja 3 kg de mandiocas e que essa balança tenha um
massor de 0,6 kg. Para que se atinja o equilíbrio, a distância d do massor em relação ao ponto
P deverá ser, em cm,
a) 16.
b) 20.
c) 24.
d) 36.
e) 40.
9. (Ufpb 2012) Um navio cargueiro está sendo carregado de minério no porto de Cabedelo. O
carregamento é, hipoteticamente, feito por um guindaste, manobrado por um operador que
suspende, de cada vez, dois containers acoplados às extremidades de uma barra de ferro de
três metros de comprimento, conforme esquema a seguir:
Na última etapa do carregamento, o
container 1 é completamente preenchido
de minério, totalizando uma massa de 4
toneladas, enquanto o container 2 é
preenchido pela metade, totalizando uma
massa de 2 toneladas. Para que os
containers sejam suspensos em
equilíbrio, o operador deve prender o
gancho do guindaste exatamente no
centro de massa do sistema, formado
pelos dois containers e pela barra de
ferro.
Nesse sentido, desprezando a massa da
barra de ferro, conclui-se que a distância
entre o gancho (preso na barra pelo
operador) e o container 1 deve ser de:
a) 0,5 m
b) 1,0 m
c) 1,5 m
d) 2,0 m
e) 2,5 m
www.nsaulasparticulares.com.br
Página 4 de 10
10. (Upe 2011) A figura abaixo mostra uma barra homogênea de peso 10 N e de comprimento
10 m que está apoiada sobre um suporte distante de 3,0 m da sua extremidade esquerda.
Pendura-se um bloco de massa m = 2,0 kg na extremidade esquerda da barra e coloca-se um
bloco de massa M = 4,0 kg sobre a barra do lado direito ao suporte. O valor de D, para que a
barra esteja em equilíbrio, em metros, vale
Dado: considere a aceleração da gravidade g = 10m / s
a) 4,5
b) 5,0
c) 5,5
d) 6,0
e) 6,5
2
www.nsaulasparticulares.com.br
Página 5 de 10
Gabarito:
Resposta da questão 1:
[E]
Dado: m C = 70 kg.
Da figura, as distâncias de Isabela e Carlos até o eixo de rotação são, respectivamente: bI =2,5
m e bC =2,0 m.
Para que a barra esteja em equilíbrio, o somatório dos momentos deve ser nulo.
M  0
 mI g bI  mC g bC  m I 
mC bC
bI

70  2

2,5
m I  56 kg.
Como o apoio está entre as forças aplicadas, o tipo de alavanca formado pela gangorra é
interfixa.
Resposta da questão 2:
[D]
| NA | .2,0 | P | .1,8
| NA | .2,0  80.10.1,8
| NA | .2,0  80.18
| NA | 80.9
 | NA | 720N
www.nsaulasparticulares.com.br
Página 6 de 10
Resposta da questão 3:
[B]
Como o andaime permanece em equilíbrio, podemos afirmar que
Analisando
F  0 :
F  0 e  M  0 .
P : peso do limpador;
P ' : peso do andaime;
T : tensão no cabo 1;
T ' : tensão no cabo 2.
 F  0  T  T ' P  P '  0   T  T '  P  P '  0  T  T '  P  P '
P  P '  cons tan te  T  T '  cons tan te
Condição que é satisfeita pelas alternativas [A] e [B] apenas.
Como T  T '  cons tante , podemos concluir que o aumento da tensão no cabo 2 corresponde
à mesma diminuição da tensão no cabo 1, condição esta satisfeita apenas pela alternativa [B].
Resposta da questão 4:
[B]
Desenhando todas as forças que atuam na barra, bem como a localização do ponto O, e
adotando como positivo o sentido horário de rotação, teremos:
Sendo:
Pb : peso da barra;
PQ : peso da esfera;
N A : Força normal trocada com o apoio A;
NB : Força normal trocada com o apoio B.
www.nsaulasparticulares.com.br
Página 7 de 10
Considerando que a soma dos momentos de todas as forças, em relação ao ponto O, é igual à
zero (condição de equilíbrio), teremos:
(m)o  0

(mN )o  (mP )o  (mP )o  (mN )o  0
B
b
Q
A
NB .2  Pb .1  PQ .0,4  NA .0  0
NB .2  50.1  80.0,4  0  0
NB .2  50  32  0
NB .2  82  0
NB  41N
Resposta da questão 5:
[A]
Como a barra está em equilíbrio, o somatório dos momentos no sentido horário é igual ao
somatório dos momentos no sentido anti-horário. Assim, analisando a figura com polo em D:
 Mhor   Mantihor
 P  3  x   FC  6  x 
300  3  x   120  6  x 

 5 3  x   2 6  x  
15  5 x  12  2 x  3 x  3 
x  1m.
Resposta da questão 6:
[A]
Como a vara está em equilíbrio de rotação, o momento resultante deve ser nulo. Assim, a
somatória dos momentos horários é igual à somatória dos momentos anti-horários.
Tomando como polo o ponto de apoio da pata direita do gato, temos:
 Mhorário   Mantihorário
0,2F  1  14  F 
 0,4 1,8  0,5  0,2   20  0,5  0,2   F  0,2  
15
 F  75 N.
0,2
Resposta da questão 7:
[D]
Desconsiderando o peso do objeto, sendo F1 a intensidade das forças pedidas, do equilíbrio,
temos:
M F  M F  F1  5  10  2  F1  4 N.
1
www.nsaulasparticulares.com.br
Página 8 de 10
Resposta da questão 8:
[E]
Dados: M = 3 kg; m = 0,6 kg; D = 8 cm.
De acordo com ao enunciado:
MDmd  d
M D 3  8 24


m
0,6 0,6

d  40 cm.
Resposta da questão 9:
[B]
Dados: L = 3 m; m 2 = M = 2 toneladas; m 1 = 2 M = 4 toneladas.
A figura mostra as forças agindo no conjunto.
Se conjunto está em equilíbrio de translação, a resultante das forças é nula:
T  P1  P2  2 M g  M g  T  3 M g.
Se o conjunto está em equilíbrio de rotação, o torque (momento) resultante é nulo:
Em relação ao ponto A, temos:
Mhor  Mantihor
A
A
 MP  MT
2
 P2 L  T x  M g  3   3 M g x 
x  1 m.
www.nsaulasparticulares.com.br
Página 9 de 10
Resposta da questão 10:
[D]
A figura abaixo mostra as forças que agem na barra e as distâncias relevantes.
Para que a barra esteja em equilíbrio, é necessário que
MFO  0 .
Então: 40(7  D)  10x2  20x3  280  40D  40  40D  240  D  6m .
www.nsaulasparticulares.com.br
Página 10 de 10