Dispositivos Eletrônicos
Aula 02: Princípios de Condução de
Corrente Elétrica em Sólidos
1
Plano da Aula
• Condutores, Isolantes e Semicondutores
• Propriedades do Silício Intrínseco
• Dopagem e seus efeitos
• Deriva e difusão de portadores
2
Condutores, Isolantes e
Semicondutores
Para o àtomo de hidrogênio
isolado, Bohr obteve os
seguintes valores de energia
do elétron para os estados
estacionários:
mq 4 1 − 13,6eV
En = −
=
2 2
2
n2
8ε 0 h n
1 eV = 1,602E-19 J, n é o número quântico
Ao aproximarmos 2 átomos, os elétrons
(sobretudo os mais externos) começam
a “sentir a presença” dos vizinhos.
EY
-{
EX
-{
E1=-13,6eV
E2=-3,4eV
E3=-1,5eV ...
3
Fonte: Fundamentos de Física; Halliday – Resnick - Walker
Condutores, Isolantes e
Semicondutores
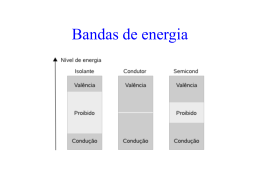
Possíveis configurações da ocupação das bandas de
energia, com vistas à condutividade elétrica:
parcialmente ocupada totalmente ocupada
Condutor
Ordens de grandeza
num condutor típico:
≈1022,1023 átomos/cm3
≈1022,1023 portadores/cm3
Semicondutor:Eg≈1eV
Isolante:Eg>>1eV
Eg é o Bandgap, a faixa
de energia proibida:
Os portadores de carga em um
metal são elétrons “livres” que
“flutuam” no “mar de íons”
Fonte: Physics of Semiconductor 4
Devices, Simon Sze
Condutores, Isolantes e
Semicondutores
Elementos de
interesse:
“Sopinha de letras” :
Si, SiGe, SiC, InP,
GaAs, GaInP, GaN, ...
Cada tecnologia com
seus prós e contras:
custo, frequência,
potência, integração,
...
5
Semicondutor
intrínseco
Como são gerados, quantos e quais são os
portadores de carga em um semicondutor?
1º Processo de geração: geração térmica (T>0K):
Ligação
Covalente
Condução
Valência
Elétron
liberado
Processo que depende de T e de Eg. Cada elétron que salta
para a banda de condução deixa um nível vazio (lacuna, no
inglês: “hole”) na banda de valência. Adotaremos:
n=densidade de elétrons p=densidade de lacunas
6
Semicondutor
intrínseco
Ocupação das lacunas por elétrons “vizinhos”:
Observe o deslocamento da lacuna! Elétrons e lacunas têm
movimento frenético aleatório. Eventualmente se
encontram: processo de recombinação (o elétron e a
lacuna se aniquilam!)
A recombinação é proporcional ao número de elétrons e
lacunas. Em equilíbrio termodinâmico, o processo de geração
térmica é compensado pelo processo de recombinação.
7
Semicondutor
intrínseco
No semicondutor intrínseco (“puro”), para
cada elétron na banda de condução temos
uma lacuna na banda de valência:
n(dens. elétrons)=p(dens. lacunas)=ni=pi
− Eg
3/ 2
ni ∝ T exp
electrons / cm 3
2 kT
Compare:
ni (T = 300 K ) ≈ 1010 electrons / cm 3
ni (T = 600 K ) ≈ 1015 electrons / cm 3
IMPORTANTE!: n⋅p=ni2≈1020 (Si, 300K)
em equilíbrio termodinâmico
Fonte: Physics of Semiconductor
Devices, Simon Sze
8
Semicondutor
intrínseco
Você deve estar se perguntando: se os bons
condutores têm ≈1012 mais portadores que o
silício intrínseco @300K, pra que serve o silício
intrínseco?
9
Dopagem
2º processo de geração de portadores: a dopagem é o processo
controlado de introdução de “impurezas” no semicondutor outrora
intrínseco, para alterar suas propriedades elétricas. O semicondutor
dopado é chamado de extrínseco.
Neste exemplo, alguns átomos de Si foram substituídos
por átomos de P (ND impurezas/cm3): na temperatura
ambiente, praticamente todos estes átomos “doam” o
5º elétron ao retículo: o semicondutor extrínseco é de
tipo N!
Lembrando: n⋅p≈1020 (Si, 300K) em
equilíbrio termodinâmico (permanece
válido c/ dopagem)
Se o Si é dopado com 1016 átomos de P por
cm3 (ND=1016) qual o valor de n? E o de p?
10
Dopagem
Neste exemplo, alguns átomos de silício
foram substituídos por átomos de Bóro (NA
impurezas/cm3):
na
temperatura
ambiente, praticamente todos estes
átomos “aceitam” elétrons do retículo
para ficarem com 8 na última camada
(gerando lacunas em excesso), o
semicondutor extrínseco é de tipo P!
Lembrando: n⋅p≈1020 (Si, 300K)
em equilíbrio termodinâmico
(permanece válido c/ dopagem)
Se o Si é dopado com 1015
átomos de B por cm3 (NA=1015)
qual o valor de n? E o de p?
11
Dopagem
Semicondutor Instrínseco
Elétron de
valência
Ligação
Covalente
Semicondutor Extrínseco
Cristal de Silício
ND doadores/cm3
Dopante
tipo N
(Doador)
O átomo dopante é
preso ao retículo,
enquanto o elétron
(tipo N) ou lacuna
(tipo P) criados são
liberados!!
Portador
Majoritário
(livre)
Densidades usuais de
dopagem: 1014 a 1018
átomos/cm3
Cristal de Silício
NA aceitadores/cm3
Portador Majoritário
(livre)
Dopante
tipo P
(aceitador)
12
Dopagem
np = ni
Portadores majoritários:
p ≈ NA
Portadores minoritários:
n
n≈ i
NA
Tipo N Portadores majoritários:
n ≈ ND
Portadores minoritários:
n
p≈ i
ND
Tipo P
2
2
Equações
válidas
em
equilíbrio
termodinâmico
2
Acabamos aqui os mecanismos de geração de portadores,
mas existem outros: por exemplo pares elétron-lacuna
criados por fótons, mecanismo que pode ser aproveitado
para a construçao de um Resistor Variável com a Luz (LDR,
do
inglês,
Light
Dependent
Resistor).
Veja:
http://en.wikipedia.org/wiki/Photoresistor
13
Deriva e difusão de
portadores
Sim, mas agora que eu sei quem são e
quantos são os portadores, como eles se
mexem??
Dois mecanismos a serem considerados para o
cálculo da densidade de corrente (J):
J total = J drift _ total + J diff _ total
Densidade de
corrente
de
deriva (drift)
Densidade
de corrente
de difusão
14
Deriva de portadores
Os portadores de carga têm movimento frenético. No silício
a 300K, há velocidades da ordem de 360.000km/h e tempo
entre colisões com o retículo da ordem de 1ps.
Em média, quantos Angstrons (10-10m) são percorridos entre colisões?
Quando um campo elétrico é aplicado, os portadores
continuam frenéticos, mas adquirem componente ordenada
→
→
“proporcional” ao campo:
vh = µ p E Velocidade média das lacunas
→
→
ve = − µ n E Velocidade média dos elétrons
µp : mobilidade das lacunas
µn : mobilidade dos elétrons
Unidades: m2V-1s-1 ou cm2V-1s-1
15
Deriva de portadores
→
→
Campo elétrico moderado!
vh = µ p E
→
→
ve = − µ n E
A mobilidade varia com
a dopagem:
Fonte: Physics of Semiconductor Devices, Simon Sze
O Razavi adota: µn = 1350cm2V-1s-1 , µp = 480cm2V-1s-1
16
Deriva de portadores
→
→
vh = µ p E
→
Campo elétrico moderado!
→
ve = − µ n E
A mobilidade varia
com a temperatura:
Fonte: Physics of Semiconductor Devices, Simon Sze
17
Deriva de portadores
→
→
vh = µ p E
→
→
ve = − µ n E
Dopagens baixas
A
velocidade
só
é
proporcional ao campo até
valores “moderados” de
campo (até ≈1kV/cm). A
partir daí, a velocidade não
mais cresce linearmente
com o campo:
Fonte: Physics of Semiconductor Devices, Simon Sze
18
Variação de ρ com a
temperatura
Agora reflita:
ni (T = 300 K ) ≈ 1010 electrons / cm 3
ni (T = 600 K ) ≈ 1015 electrons / cm 3
+
300K
600K
Se uma pastilha de semicondutor intrínseco aqueçe, a resistência
aumenta ou diminui? (ver a seção “Conduction model” em
http://en.wikipedia.org/wiki/Thermistor )
Isto propicia a construção de dispositivos (NTCs) que limitam a corrente de
surto quando uma fonte é ligada à rede. Quando o dispositivo se aquece pela
passagem de corrente, sua resistência diminue, diminuindo a potência gasta.
19
Deriva de portadores
A corrente elétrica é calculada como sendo a quantidade de
carga que atravessa uma seção tranversal em 1s
Exemplo: barra de semicondutor
→
→
vh = µ p E
→
→
ve = − µ n E
Observe a polaridade da fonte: O campo elétrico na barra
aponta para direita: As lacunas se deslocam para a direita,
e os elétrons se deslocam para a esquerda!!
20
Deriva de portadores
A corrente elétrica é calculada como sendo a quantidade de
carga que atravessa uma seção tranversal em 1s
Ex. Se considerarmos apenas o deslocamento de lacunas (p):
→
→
vh = µ p ⋅ E
Corrente na barra entrando pelo lado esquerdo!
Área = W ⋅ h
r
r
(corrente de deriva
r
I
=
v
⋅
W
⋅
h
⋅
p
⋅
q
Volume / Segundo = v ⋅W ⋅ h
drift _ p
de lacunas)
r
Portadores / Segundo = v ⋅W ⋅ h ⋅ p
r
C arg a / Segundo = v ⋅ W ⋅ h ⋅ p ⋅ q
E os elétrons? Percurso contrário,
21
corrente adicional!
Deriva de portadores
A densidade é encontrada dividindo-se a corrente pela área
r
(W⋅h):
r
r
I drift _ n
J drift _ n =
= µn E ⋅ n ⋅ q
w⋅h
r
r
r
I drift _ p
J drift _ p =
= µpE ⋅ p ⋅q
w⋅h
r
r
r
r
J drift _ tot = J drift _ n + J drift _ p = q( µ n n + µ p p) E
A densidade de corrente total leva em conta os dois portadores
de carga (observe que as correntes são adicionadas já que os
portadores vão em direções contrárias e possuem cargas
opostas).
22
Difusão de portadores
Processo pelo qual partículas se movem de uma região de
maior concentração para uma região de menor
concentração. Mais uma manifestação do movimento
frenético das partículas.
Injeção de
portadores
Material semicondutor
Injeção de
portadores
Concentração não-uniforme
23
Difusão de portadores
Equações do processo (leis de difusão):
r
dn
J diff _ n = qDn
dx
Carga do
elétron
r
dp
J diff _ p = −qD p
dx
Gradiente de
“Aptidão” concentração
para difundir
Dn e Dp são as constantes de difusão de elétrons e lacunas,
respectivamente
J diff _ tot
dn
dp
= q ( Dn
− Dp
)
dx
dx
A corrente total leva em conta a difusão de elétrons
e lacunas
24
Difusão de portadores
Exemplo: Semicondutor do tipo P, iluminado por uma
fonte que gera pares elétron-lacuna na superfície
Ln = Dnτ n
2
Comprimento
de difusão dos
elétrons
no material
Constante de
difusão dos
elétrons no
material
Tempo de
vida médio
dos elétrons
no material
Ln representa a distância percorrida até que a concentração de
portadores diminua por um fator de e (2,718)
25
Difusão de portadores
Injeção de
portadores
Injeção de
portadores
J diff _ n
dn
N
= qDn
= −qDn ⋅
dx
L
J diff _ n
−x
dn − qDn N
= qD
=
exp
dx
Ln
Ln
Observe que no caso da direita, a densidade de corrente de elétrons
em x=Ln é apenas 36.7% (ouseja, 1/e) do valor em x=0!
(o que acontece com o restante dos elétrons?)
26
Deriva e difusão de
portadores
J drift _ n = µ n E ⋅ n ⋅ q
J drift _ p = µ p E ⋅ p ⋅ q
Relação
de
Einstein,
relacionando a constante
de difusão à mobilidade:
Dn
J diff _ n
dn
= qDn
dx
J diff _ p
dp
= −qD p
dx
Dp
kT
=
=
µn µ p
q
k ⋅ T 1,38 ⋅10 −23 J ⋅ K −1 ⋅ 300 K
=
≈ 25,9mV @ 300 K
−19
q
1,6 ⋅10 C
K=constante de Boltzman
T=temperatura em Kelvin
q=carga do elétron
Chamaremos esta
quantidade de VT:
“tensão térmica”
27
Resumo dos pontos
importantes
• Diferença entre condutores e semicondutores:
presença de uma banda proibida, coeficiente de
temperatura, tipos de portadores, ...
• n⋅p≈1020 (Si, 300K) em equilíbrio termodinâmico
(intrínseco ou dopado).
• A dopagem pode ser usada para mudar a
condutividade elétrica do semicondutor
• Processos de deriva e difusão de portadores
28
Cronograma de
atividades
• Não pense que você vai aprender revisando os slides:
LEIA O LIVRO! Sugere-se o seguinte cronograma:
Atividade
Duração
Razavi: Leitura do Cap. 2.1 completo
(todos os subitens)
45 minutos
Revisão dos slides
45 minutos
Resolução analítica das questões (15
minutos/questão)
60 minutos
Total: 2h30min de atividades. Se você levar muito mais
tempo do que esta previsão, converse com o professor.
29
Exercícios: trazer
próxima aula
Questão do Razavi: A concentração de portadores intrínsecos do germânio (Ge) é dado
pel seguinte expressão:
−E
ni (cm −3 ) = 1,66 ⋅10 ⋅ T
15
g
1, 5
⋅ e 2 kT
Considere Eg=0,66eV e k=8,617·10-5eV/K (=1,38·10-23J/K). Determine:
O valor de ni em 300K e em 600K, e compare com os valores encontrados para o
silício (Slide 8)
A concentração de elétrons e lacunas em 300K e em 600K, se o germânio é dopado
com fósforo a uma densidade de 5·1016 átomos/cm3.
Pode-se se dizer que a condição a 600K do germânio dopado é muito diferente da
condição do germânio intrínseco? O que se pode concluir que acontece quando o
semicondutor dopado é muito aquecido?
http://jas.eng.buffalo.edu/education/semicon/fermi/bandAndLevel/fermi.html
30
Exercícios: trazer
próxima aula
Uma barra de silício (Si) do tipo N (ND=1017imp/cm3) com 1µm de distância é submetida
a uma tensão de 0,1V. Determine:
O campo elétrico na barra, em unidades de V/cm
Observe o slide 18. O campo elétrico é baixo o suficiente pra você dizer que a
velocidade varia proporcionalmente ao campo?
A velocidade média dos elétrons (use a mobilidade no Slide 16)
O tempo médio que os elétrons levam para atravessar a barra
Se a barra tiver seção transversal de 1µm x 1µm, reponda:
Qual o valor da corrente resultante da deriva dos elétrons?
Qual o valor da corrente resultante da deriva das lacunas?
Qual o valor total da corrente na barra?
31
Exercícios: trazer
próxima aula
Uma barra de arseneto de gálio (GaAs) do tipo N (ND=1015 imp/cm3) com 1µm de
distância é submetida a uma tensão de 0,1V. Determine:
A densidade de lacunas na barra (use o ni no Slide 8)
A velocidade média dos elétrons (use a mobilidade no Slide 16)
O tempo médio que os elétrons levam para atravessar a barra
Se a barra tiver seção transversal de 1µm x 1µm, reponda:
Qual o valor da corrente resultante da deriva dos elétrons?
Qual o valor da corrente resultante da deriva das lacunas?
Qual o valor total da corrente na barra?
32
Exercícios: trazer
próxima aula
Considere a barra de silício abaixo, com seção transversal de 1µm por 1µm, na qual são
injetados elétrons e lacunas conforme a figura. Determine:
O sentido da corrente na barra
O valor da corrente total na barra
Elétrons
Lacunas
33
ANEXO 01
Processo de Geração e Recombinação
Equilíbrio termodinâmico
34
Geração-Recombinação
• Este anexo foi motivado por uma questão de
um
aluno,
que
também
pe
um
questionamento no livro do Razavi.
• A questão é: por que não é a SOMA de
(densidade de) portadores de carga n e p
(n+p) que deveria se manter constante no
equilíbrio? Por que é o produto de portadores
de carga (n·p) que se mantém constante (lei
da ação da massas)?
35
Geração-Recombinação
• A resposta é que o processo de geração térmica
(G) é dependente do bandgap Eg e da
temperatura T, enquanto que a recombinação (R)
é proporcional ao produto de n e p. E aí vem a
questão do aluno: Mas por que ao produto, por
que não à soma??
• Iremos simular as duas hipóteses e mostrar que
esta última gera uma incosistência, o fato de se
poder “matar” (recombinar) quem JÁ NÃO
EXISTE!! Vejamos!
36
Geração-Recombinação
• Vamos fazer umas contas, apenas com poucas
premissas:
– 1ª premissa: que, experimentalmente, observa-se
que, no Si, há, em 300K (~temperatura ambiente),
1010 eletrons/cm3 (o mesmo para lacunas). Qualquer
outro número poderia ser usado (exemplo, números
de outros semicondutores)
– 2ª premissa: que a geração de portadores em 300K é
de, digamos, 109 eletrons/cm3/s (o mesmo para
lacunas). Qualquer outro número poderia ser usado,
teríamos apenas que esperar mais ou menos tempo
até observar uma condição de equilíbrio.
37
Geração-Recombinação
Faremos um “experimento mental” em apenas 2
temperaturas (0K e 300K). Sabemos que a geração G depende
de Eg e de T. Como já assumimos um valor de G em 300K (109
eletrons/cm3/s, premissa 2), precisamos apenas pensar no
valor de G em 0K. Ora, no zero absoluto, é de se supor que o
processo de geração é anulado, já que não há energia
excedente para que as ligações sejam quebradas. Assim:
G (0 K ) = 0
G (300 K ) = 10 9 eletrons / cm 3 / s = 10 9 lacunas / cm 3 / s
38
Geração-Recombinação
Tratemos agora da recombinação. Adotaremos uma
PRIMEIRA HIPÓTESE: a de que o processo é propocional AO
PRODUTO das populações:
R = k3 ⋅ n ⋅ p
Nossa 1ª premissa é de que, em 300K, n=p=1010 /cm3. Além
disso, o equilíbio em 300K impõe que o processo de geração
seja compensado (“anulado”) pela recombinação (do
contrário as populações aumentariam ou diminuiriam), ou
seja, G=R. Assim:
R (300 K ) = k 3 ⋅1010 ⋅1010 = G (300 K ) ⇒ k 3 ⋅10 20 = 10 9 ⇒ k 3 = 10 −11
39
Geração-Recombinação
Recapitulando:
G = 10 9
Elétros/lacunas gerados POR SEGUNDO em 1 cm3
R = 10 −11 ⋅ n ⋅ p Elétros/lacunas recombinados POR SEGUNDO em 1 cm3
Agora vamos usar o SCILAB para determinar as populações de eletrons e lacunas
nas seguintes situações:
1- Inicialmente estamos em 0K, as populações são nulas, e não há geração ou
recombinação
2- A temperatura é “subitamente” elevada a 300K, para a qual temos G e R
definidos
3- Depois de chegarmos ao equilíbrio em 300K, iremos “dopar subitamente”
(criar) o material com impurezas aceitadoras na densidade de 1014 cm-3
4- Observaremos os valores de equilíbrio.
40
Geração-Recombinação
Código SCILAB:
clear;
// abaixo definem-se as populações para T=0K
n(1)=0;
p(1)=0;
// nesta temperatura, G, que é proporcional a T, é nula. a recombinação R, que é
// proporcional a n e a p, também é nula. Então estas quantidades representam
// os valores de equilíbrio em T=0K (n=p=0).
// “De repente”, a temperatura é aumentada para 300K. Neste caso,
// G=1e9, o que mudará as quantidades inicialmente aumentando-as,
// o que por conseguinte aumentará a recombinação, até que um valor
// de equilíbrio seja atingido.
// abaixo define-se o intervalo de simulação. Este deve ser ajustado de acordo com
// os números usados para a quantidade de geração (ou recombinação) por segundo.
interval=1e-3; // 1ms
41
Geração-Recombinação
Código SCILAB (continuação):
// faça a simulação em 15 mil pontos. Este é um número para uma simulação rápida
for i=2:1:15000, // de 2 a 15000 por passo de 1, faça:
// um intevalo de 1ms se passou. O número de portadores é agora o número
// que havia, n(i-1), somado à quantidade gerada em 1 ms, G(300K) * 1ms,
// subtraído da recombinação em 1 ms, R( n(i-1), p(i-1) ) * 1ms.
n(i) = n(i-1) + 1e9 * interval - (1e-11 * n(i-1) * p(i-1) * interval );
p(i) = p(i-1) + 1e9 * interval - (1e-11 * n(i-1) * p(i-1) * interval );
end
// até aqui, já devemos estar em um valor de equilíbrio em 300K.
// de repente, uma dopagem P é introduzida, com densidade de dopantes
// de 1e14:
p(15000)=1e14;
42
Geração-Recombinação
Código SCILAB (continuação):
// define-se um novo intervalo, pois o processo de recombinação vai ser
// muito aumentado, e é preciso que a quantidade recombinada em um
// intervalo de simulação seja INFERIOR às quantidades iniciais de portadores.
interval=1e-6; // 1us
// repita o processo até 30 mil pontos
for i=15001:1:30000,
n(i) = n(i-1) + 1e9 * interval - (1e-11 * n(i-1) * p(i-1) * interval );
p(i) = p(i-1) + 1e9 * interval - (1e-11 * n(i-1) * p(i-1) * interval );
end
43
Geração-Recombinação
Código SCILAB (continuação):
// plote as quantidades
plot2d([n p],rect=[1,1e3,30000,1e15],logflag="nl", leg="densidade de
eletrons@densidade de lacunas");
set(gca(),"grid",[1 1]); // incluindo o grid.
a=gca();
poly1= a.children(1).children(1);
poly1.thickness=3;
poly2= a.children(1).children(2);
poly2.thickness=3;
poly2.foreground=5;
Resultados na próxima página!
44
Geração-Recombinação
Disturbio com a introdução de
1014 dopantes/cm3 (aceitadores)
Valor de equilíbio em 300K
EXTRÍNSECO
(106 eletrons, 1014 lacunas)
Valor de equilíbio em 300K
INTRINSECO
(1010 eletrons, 1010 lacunas)
45
Geração-Recombinação
Trataremos agora da SEGUNDA HIPÓTESE: a de que o
processo de recombinação é propocional À SOMA das
populações:
R = k 4 ⋅ (n + p )
Tal como no caso da primeira hipótese, devemos igualar a
recombinação em 300K com a geração (que é a mesma):
R (300 K ) = k 4 ⋅ (1010 + 1010 ) = G (300 K ) ⇒ k 4 ⋅ 2 ⋅1010 = 10 9 ⇒ k 4 = 0.05
46
Geração-Recombinação
Recapitulando:
Elétros/lacunas gerados POR SEGUNDO em 1 cm3
G = 10 9
R = 0.05 ⋅ ( n + p ) Elétros/lacunas recombinados POR SEGUNDO em 1 cm3
Faremos uma simulação das mesmas
condições!
47
Geração-Recombinação
Código SCILAB:
clear;
// abaixo definem-se as populações para T=0K
n(1)=0;
p(1)=0;
// abaixo define-se o intervalo de simulação.
interval=2e-3; // 2ms. Mudado pois neste caso o processo é mais lento
// faça a simulação em 15 mil pontos.
for i=2:1:15000, // de 2 a 15000 por passo de 1, faça:
// um intevalo de 2ms se passou. O número de portadores é agora o número
// que havia, n(i-1), somado à quantidade gerada em 2 ms, G(300K) * 2ms,
// subtraído da recombinação em 2ms, R(n(i-1), p(i-1)) * 2ms.
n(i) = n(i-1) + 1e9 * interval - (0.05 * (n(i-1) + p(i-1)) * interval );
p(i) = p(i-1) + 1e9 * interval - (0.05 * (n(i-1) + p(i-1)) * interval );
end
48
Geração-Recombinação
Código SCILAB:
// até aqui, já devemos estar em um valor de equilíbrio em 300K.
// de repente, uma dopagem P é introduzida, com densidade de dopantes
// de 1e14:
p(15000)=1e14;
// define-se um novo intervalo, pois o processo de recombinação vai ser
// muito aumentado, e é preciso que a quantidade recombinada em um
// intervalo de simulação seja INFERIOR às quantidades iniciais de portadores.
interval=1e-6; // 1us
// repita o processo
for i=15001:1:30000,
n(i) = n(i-1) + 1e9 * interval - (0.05 * (n(i-1) + p(i-1)) * interval );
p(i) = p(i-1) + 1e9 * interval - (0.05 * (n(i-1) + p(i-1)) * interval );
end
49
Geração-Recombinação
Código SCILAB:
// plote as quantidades
plot2d([n p],rect=[1,1e3,30000,1e15],logflag="nl", leg="densidade de eletrons@densidade
de lacunas");
set(gca(),"grid",[1 1]); // incluindo o grid.
a=gca(); poly1= a.children(1).children(1); poly1.thickness=3;
poly2= a.children(1).children(2); poly2.thickness=3; poly2.foreground=5;
scf(); // Pra ver o que houve na plotagem logarítmica...
// plote as quantidades
plot2d([n p],rect=[1,-1e11,30000,1e10],logflag="nn", leg="densidade de
eletrons@densidade de lacunas");
set(gca(),"grid",[1 1]); // incluindo o grid.
a=gca(); poly1= a.children(1).children(1); poly1.thickness=3;
poly2= a.children(1).children(2); poly2.thickness=3; poly2.foreground=5;
50
Geração-Recombinação
Disturbio com a introdução de
1014 dopantes/cm3 (aceitadores)
Valor de equilíbio em 300K
INTRINSECO
(1010 eletrons, 1010 lacunas)
Valor de equilíbio em 300K
EXTRÍNSECO
(1014 lacunas, ??????)
O que houve ???
51
Geração-Recombinação
Eixo vertical linear
Disturbio com a introdução de
1014 dopantes/cm3 (aceitadores)
A população de
eletrons se torna
NEGATIVA!!!
Ou seja, estamos
“matando”
(recombinando)
quem já está morto
(não existe)!!!
52
Geração-Recombinação
Conclusão: a SEGUNDA HIPÓTESE
leva a uma INCONSISTÊNCIA!
E por que não
R = k5 ⋅ n ⋅ p ?????
2
2
Reflita e Simule!
53