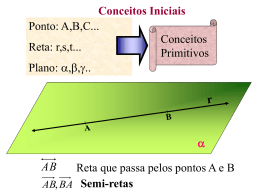
GEOMETRIA PLANA
1 - INTRODUÇÃO
Geometria é uma palavra de origem grega e que
significa “medida de terra”.
Geometria, como um dos ramos da Matemática,
estuda as figuras geométricas e suas propriedades.
Os conceitos previamente estabelecidos, em Geometria, são conceitos não-definidos, são as noções primitivas.
Classificando os segmentos de reta, tem-se segmentos de reta que são:
a) Consecutivos: “tem uma extremidade comum”.
B
C
B
B
A
C
A
C
A
São consecutivos os segmentos de reta AB e BC
2 - NOÇÕES PRIMITIVAS
b) Colineares: “estão contidos numa mesma reta”.
D
Ponto
Reta
Plano
Entes primitivos
As noções primitivas estabelecem as Propriedades
Geométricas, que são classificadas em:
I) Axiomas - propriedades aceitas sem demonstração.
II) Teoremas - propriedades que são demonstradas (deduzidas)
A
P
M
M
AB e CD
MN e NP
NN e NP
c) Adjacentes: “são colineares, são consecutivos
e possuem apenas um ponto comum”.
C
B
A
AB e BC
3 - NOTAÇÕES
•A
• Ponto
N
N
B
Pertinência
Inclusão
Relações primitivas
P
C
Segmentos de Reta Congruentes: AB ≡CD , lêse AB é congruente a CD se as medidas de AB e
r
• Reta
CD são iguais.
Ponto médio de um segmento de reta
B
• Plano
Sendo AM≡MB , o ponto M é o ponto
médio de AB .
M
A
(α)
• Semi-reta
⇓
4 - ÂNGULO
B
A
q Conceito:
AB : de origem A
Ângulo é a região plana formada por duas semiretas de mesma origem.
A
BA : de origem B
Vértice 0
• Segmento de reta
⇓
B
A
Ângulo A 0̂ B :
Lados
0
0A
0B
AB ou BA
B
q Classificação
a) Consecutivos: Dois ângulos são consecutivos
se têm um lado comum.
d) Ângulos complementares: Dois ângulos são
complementares se a soma de suas medidas é 90º.
A
B
A
A 0̂B é xº
A
Medida do
x
B
0
0
B 0̂C é yº
y
C
0
C
C
B
x + y = 90º então os ângulos A 0̂B e B 0̂C são complementares.
( )
A 0̂B e B 0̂C são consecutivos, lado 0B é comum.
b) Adjacentes: Dois ângulos consecutivos são
adjacentes se não possuem pontos internos comuns.
( )
( )
m A0̂B + m B0̂C = m A0̂C = 90º ⇒ A0̂C é
denominado “ângulo reto”.
e) Ângulo suplementares: Dois ângulos são suplementares se a soma de suas medidas é 180º.
A
A
0
B
A 0̂B e B 0̂C são ângulos
adjacentes
y
x
0
C
c) Ângulos opostos pelo vértice (o. p. v.): Dois
ângulos são opostos pelo vértice quando os lados de
um deles são semi-retas opostas aos lados do outro.
D
D
B
(
)
m A 0̂B = x º
0
C
(
m C 0̂D
⇓
) = yº
xº + yº = 180º então os ângulos A 0̂B e C0̂D são
suplementares.
A
B
A 0̂B e C0̂D são ângulos
opostos pelo vértice.
0
A
C
C
0
B
A 0̂B e B 0̂C são adjacentes suplementares. Os lados
Os ângulos o. p. v. são congruentes, isto é, são ângulos que têm medidas iguais.
Uma das medidas de ângulo é o grau.
Ex.: Medida do ângulo A 0̂B é 30º.
(
( )
m A0̂B =30º
B
f) Ângulo agudo: é todo ângulo menor que um
ângulo reto.
)
Se A 0̂ B é agudo, m A 0̂B < 90 º
A
30 º
( ) ( ) ( )
m A0̂B +m B0̂C =m A0̂C =180º⇒A0̂C é denomina-
do “ângulo raso” ou ângulo de “meia volta”.
1º = 60’ e 1’ = 60”
0
não-comuns são semi-retas opostas. ( 0A e 0C )
g) Ângulo obtuso: é todo ângulo maior que um
ângulo reto e menor que um ângulo raso.
(
)
Se A 0̂B é obtuso, 90 º < m A 0̂B < 180 º :
q Bissetriz
Bissetriz de um ângulo é a semi-reta com origem
no vértice do ângulo, interna ao ângulo, e que o divide
em dois ângulos adjacentes congruentes.
A
EXERCÍCIOS
RESOLVIDOS
01) Dados AB = 4cm e CD = 32cm, determine a medida de CD em função de AB.
0M é bissetriz de A 0̂ B
M
0
( )
Solução:
AB = 4cm e CD = 32cm ⇒ 32 : 4 = 8 ou seja
m(CD) = 8 . m(AB)
⇓
( )
m A0̂M = m B0̂M
B
q Propriedade da Bissetriz de um Angulo
“Todo ponto da bissetriz de um ângulo é eqüidistante
dos lados do mesmo”
02) Dados A, B e C colineares, com B entre A e C, tais
que AB seja o tríplo de BC, calcule as medidas de
AB e de BC, sabendo que AC mede 32cm.
Solução:
q Retas
A
Concorrentes ⇒ possuem apenas um ponto comum
Como AC = AB + BC ⇒ 3x + x = 32 ⇒ x = 8cm
Logo, BC = 8cm e AB = 24cm
r ∩ s = {P}
03) Dados A, B, e C colineares, com B entre A e C e
sendo M e N os pontos médios de AB e BC, respectivamente, determine MN em função de AB e BC.
s
Perpendiculares ⇒ interceptam-se segundo
ângulos retos
Solução:
s
A
r
M
MB =
r⊥s
q Mediatriz
Mediatriz de um segmento de reta é a reta perpendicular ao segmento passando pelo ponto médio do
mesmo.
B
M
04) O ângulo formado pela bissetriz de dois ângulos
adjacentes mede 39º. Se um dos ângulos mede, 42º,
determine a medida do outro.
Solução:
r
A
x
0
B
N
C
Qualquer ponto da reta mediatriz de AB é
(
)
0M bissetriz A 0̂B
0N bissetriz B 0̂C
x
y
y
mediatriz de AB .
eqüidistante dos extremos de AB .
A0̂B e B0̂C⇒ adjacentes
M
AM ≡ MB
r ⊥ AB , é a reta
C
AB BC
AB + BC
+
ou MN =
2
2
2
A
⇓
N
AB
BC
, BN =
e MN = MB + BN
2
2
Logo, MN =
B
C
Se BC = x ⇒ AB = 3x
r
P
B
(
)
m M 0̂N = 39 º
( )
m (B 0̂C ) = 2 y ?
Se m A0̂B = 42º ⇒ x = 21º
m M0̂N = x + y ⇒ 21º + y = 39 º ⇒ y = 18 º
( )
Logo, m B0̂C = 2 ⋅ 18 º = 36 º
Resp.) 36º
05) Determine a medida do ângulo que é o dobro do
seu suplemento.
Solução:
Ângulo de medida x ⇒ medida do seu suplemento
(180º - x)
x = 2(180º - x) ⇒ 3x = 360º ⇒ x = 120º
Resp.) 120º
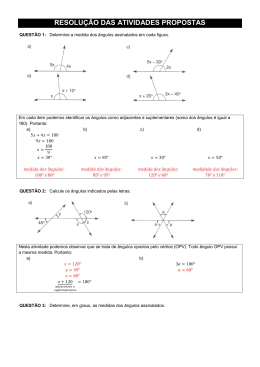
04) Observe a figura.
( )
m r0̂ s = 90 º
s
4x
Determine o valor de x.
3x
2x
0
r
Resp.) 10º
06) Calcule a medida de um ângulo que é igual a 2/3 de
seu complemento.
TESTES
Solução:
x = 2 (90º−x)⇒ 5x =180 º⇒ x = 36º
3
Resp.) 36º
07) Dois ângulos são adjacentes e medem 43º 23’ 17”
e 28º 35’ 23”. Determine a medida do ângulo formado por suas bissetrizes.
Solução:
43º 23’ 17” +
28º 35’ 23”
71º 58’ 40”
71º 58’ 40”
2
11
35º 59’ 20”
1º = 60’
11 8’ 40”
18 0
0
Resp.) Ângulo formado pelas bissetrizes mede
35º 59’ 20”
EXERCÍCIOS
PROPOSTOS
01) Efetue:
a) 18º 35’ 27” + 32º 47’ 35” Resp.) 51º 23’ 02”
b) 87º 13’ 27” - 23º 47’ 38” Resp.) 63º 25’ 49”
c) 13º 42’ 28” x 5
Resp.) 68º 32’ 20”
d) 73º 25’ 47” : 2
Resp.) 36º 42’ 53,5”
02) Determine a medida de um ângulo se a quinta parte do seu suplemento vale 24º.
Resp.) 60º
03) Calcule a medida do ângulo que excede seu complemento em 43º.
Resp.) 66º 30’
01) O complemento de 12º 37’ 42” mede:
a) 78º 23’ 18”
b) 77º 22’ 18”
c) 78º 22’ 18”
d) 78º 23’ 17”
02) O ângulo que mede a metade de seu complemento
é o ângulo de:
a) 60º
b) 50º
c) 40º
d) 30º
03) A medida do ângulo igual ao triplo de seu complemento é igual a:
a) 60º
b) 66º 20’
c) 67º 30’
d) 69º
04) A medida do suplemento do ângulo de 93º 15’ é:
a) 86º 45’
b) 87º 15’
c) 86º 15’
d) 87º 45’
05) Classificando verdadeira com V e falso com F as
afirmações:
I) Dois ângulos consecutivos são adjacentes.
II) Dois ângulos adjacentes são consecutivos.
III) Dois ângulos O. P. V. são adjacentes.
Obtém-se a sequência.
a) VFF
b) FVF
c) VVF
d) FFV
06) O ângulo formado pelas bissetrizes de dois ângulos adjacentes mede 40º. Sendo um deles igual a
três quintos do outro, a medida do maior desses
ângulos é:
a) 15º
b) 25º
c) 30º
d) 50º
07)
13) As medidas de dois ângulos opostos pelo vértice são
expressas, em graus, por (3x + 40º) e (6x - 21º). A
medida x é igual a:
a) 20º 12’
b) 12º 20’
c) 20º 20’
d) 12º 12’
08)
14) Observe a figura, onde 0E é bissetriz de D0̂B .
C
D
E
20º
09) Os pontos A, B e C são colineares com C entre A
e B. Se os pontos M e N são pontos médios de AB
e BC, então MN é igual a:
a)
AB + AC
2
b)
AB − BC
2
AB + BC
c)
2
d)
AB − AC
2
10) São dados os segmentos AB, CD, EF e GH , proporcionais
nessa ordem. Se AB = (x + 1) cm , CD = (x + 8) cm ,
EF = (x + 10) cm e GH = (x + 20) cm , podemos afirmar
que a soma das medidas AB + CD + EF + GH vale, em cm
a) 98
b) 109
c) 119
d) 129
11) Seja o segmento MN e Q ∈ MN tal que
MQ 5
= .
QN 9
Se o ponto Q está situado a 15cm da extremidade
M do segmento MN , a medida de MN , em cm, é:
a) 48
b) 42
c) 36
d) 27
12) Dois segmentos são tais que um deles mede 2m e
o outro mede 80cm. A razão entre o maior e o menor desses segmentos é:
a) 5/2
b) 5/4
c) 40
d) 4
0
A
B
A medida de A 0̂C , é
a) 20º
b) 50º
c) 70º
d) 140º
15) Duas retas concorrentes formam entre si um ângulo de 112º. A medida dos outros ângulos agudos
que essas retas formam entre si, mede
a) 58º
b) 68º
c) 78º
d) 112º
16) Dois ângulos adjacentes complementares têm medidas expressas por 2x e x + 42º. As medidas desses ângulos, são
a) 32º e 58º
b) 42º e 48º
c) 44º e 46º
d) 52º e 38º
17) As medias de dois ângulos congruentes são expressas por (3x + 20º) e (5x - 34º). A medida desses ângulos, é:
a) 27º
b) 91º
c) 101º
d) 110º
GABARITO
01)
06)
11)
16)
B
A
B
A
02)
07)
12)
17)
D
E
A
C
03) C
08) E
13) C
04) A
09) B
14) B
05) B
10) C
15) B
ORVILE CARNEIRO
5 - PARALELAS TRANSVERSAIS E ÂNGULOS
q Retas Concorrentes - Definição
Duas reta são concorrentes se, e somente se,
elas têm um único ponto comum.
r I s = {P}
q Propriedades do Paralelismo
r//s
t
1 2
4 3
5 6
8 7
r
s
P
Se duas retas r e s, paralelas, são cortadas por uma
transversal t;
1 - os ângulos correspondentes são
congruentes.
s
r
q Retas Paralelas - Definição
Duas retas são paralelas (Símbolo: //) se, e somente se, são coincidente (iguais) ou são coplanares e não
têm nenhum ponto comum.
b
a
a = b ⇒ a // b
(a ⊂ α , b ⊂ α , a I b = ∅) ⇒ a // b
a
b
α
Sejam a e b duas retas paralelas ou não e t uma
reta concorrente com a e b.
1) t é uma transversal de a e b.
4 3
a
2
5 6
8 7
t
a
b
2 - os pares de ângulos alternos internos são
congruentes.
3̂ e 5̂ ⇒ 3̂ ≡ 5̂
ângulos alternos internos
4̂ e 6̂ ⇒ 4̂ ≡ 6̂
3 - os pares de ângulos alternos externos são
congruentes.
1̂ e 7̂ ⇒ 1̂ ≡ 7̂
ângulos alternos externos
2̂ e 8̂ ⇒ 2̂ ≡ 8̂
4 - os pares de ângulos colaterais internos são
suplementares.
3$ e 6$ ⇒ 3$ + 6$ = 180 o
ângulos colaterais internos
4$ e 5$ ⇒ 4$ + 5$ = 180 o
5 - os pares de ângulos colaterais externos
são suplementares.
t
b
1
1̂ e 5̂ ⇒ 1̂ ≡ 5̂
4̂ e 8̂ ⇒ 4̂ ≡ 8̂
Ângulos correspondentes
2̂ e 6̂ ⇒ 2̂ ≡ 6̂
3̂ e 7̂ ⇒ 3̂ ≡ 7̂
1 2
4 3
5 6
8 7
1$ e 8$ ⇒ 1$ + 8$ = 180 o
ângulos colaterais externos
2$ e 7$ ⇒ 2$ + 7$ = 180 o
ORVILE CARNEIRO
MATEMÁTICA
04) Observe a figura, sendo r // s.
EXERCÍCIOS
RESOLVIDOS
t
01) Observe a figura, onde r // s
r
120º
t
x
r
70º
z
y
s
x +x
3
s
Calcule o valor da medida x:
Solução:
Determine: x̂ + ŷ − ẑ
x
+ x + 120 º = 180 º
3
Solução:
x̂ = 70º (o. p. v.)
⇓
ŷ = 70 º (alternos internos)
ẑ + 70º = 180º (colaterais internos) ⇒ ẑ = 110º
x̂ + ŷ − ẑ = 70 º + 70 º − 110 º ⇒ x̂ + ŷ − ẑ = 30 º
02) Mostre que ângulos de lados paralelos são
congruentes ou suplementares.
4x
= 60º ou x = 45º
3
Resp.) 45º
05) Dois ângulos alternos internos formados por duas
retas paralelas cortadas por uma reta transversal,
são expressos por 2x e 3x - 20º. Determine a medida dos ângulos colaterais internos formados por essas retas.
Solução
A
C
α
PA // QC
PB // ED
x
P
B
M
θ
E
β
Solução:
2x = 3x - 20º (alternos internos)
⇓
x = 20º ⇒ cada alterno interno mede 40º (colaterais
internos são suplementares).
Um dos ângulos internos mede 40º e o colateral
interno correspondente 140º.
Resp.) 40º e 140º
Q
D
Logo, αˆ = βˆ
EXERCÍCIOS
PROPOSTOS
II) αˆ =βˆ e βˆ + θˆ =180º ⇒ αˆ + θˆ =180º
01) Observe a figura, sendo a // b e c um transversal
I) αˆ = x̂ (correspondentes) e βˆ = x̂ (correspondentes).
c
03) A soma das medidas dos quatro ângulos agudos
formados por duas retas paralelas cortadas por uma
reta transversal é igual a 120º.
Determine a medida de cada ângulo obtuso formado
por essas retas.
x
Solução:
120º : 4 = 30º
180º - 30º = 150º
x
y
Resp.) 150º
x
α
θ
Calcule x
x
Resp.) 7º 12’
a
b
Dados:
α = 8x + 9º
θ = 17x - 9º
ORVILE CARNEIRO
02) Observe a figura, onde r //s e t é uma transversal
t
07) Calcule o valor de x, sendo r//s.
r
40o
r
2x
3x - 20º
112o
s
y + 10º
x
Determine o valor de (x + y)
s
Resp.) 72º
Resp.) 50º
03) Observe a figura onde os ângulos de medidas α e
β têm lados paralelos.
Sendo α = 8x e β = 2x + 30º, determine o suplemento de β.
08) Se r//s, calcule α
110o
α
s
α
r
30o
Resp.) 100º
β
09) Na figura abaixo, as retas r e s são paralelas,
calcule α .
Resp.) 140º
A
04) Calcule o valor de x + y, sendo r//s e t//v.
r
3α
t
v
100o
60º
r
B
2α
y
s
x
s
C
Resp.) 52º
Resp.) 180º
05) Na figura abaixo, ED é paralela a BC . Sendo BÂE
10) Na figura, calcule a medida do ângulo α , sendo r//s.
igual a 80º e AB̂C igual a 35º, calcule a medida de AÊD.
) 30o
80º
D
80o
E
)α
35º
B
r
)
A
C
06) Determinar o valor de x, sendo r//s.
70o
Resp.) 100º
)
r
3x
s
4x
Resp.) 10º
50o
)
s
Resp.) 115º
ORVILE CARNEIRO
MATEMÁTICA
05) Na figura, sendo r // s, o ângulo α mede:
TESTES
α
01) Observe a figura, sabendo que as retas r e s são
paralelas.
r
80º
x
20º
O valor de x, é:
a) 100º
b) 110º
3x
2x
120º
r
s
a) 142º
b) 146º
c) 144º
d) 148º
s
c) 120º
d) 130º
06) Na figura, 0M é a bissetriz do ângulo A 0̂B , 0N é a bissetriz
02) Observe a figura, sendo r // s
do ângulo B0̂C e o 0P é a bissetriz do ângulo C0̂D . A
r
soma P0̂D + M0̂N é:
30º
x
60º
N
70º
C
s
O valor de x, é:
a) 90º
b) 100º
c) 130º
d) 150º
B
P
M
03) Observe a figura, sendo r // s.
D
r
0
a) 90º
b) 60º
c) 45º
d) 30º
x
s
40º
GABARITO
01) A
06) C
O valor de x, é:
a) 30º
b) 40º
c) 50º
d) 60º
r
60º
A medida do ângulo x, é:
a) 50º
b) 70º
x
s
c) 110º
d) 130º
02) B
07) A
03) C
08) D
ANOTAÇÕES
04) Observe a figura onde r // s.
70º
A
04) D
05) C
Baixar