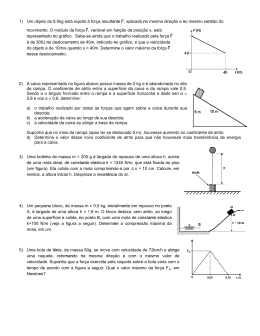
Universidade Comunitária da Região de
Chapecó – UNOCHAPECÓ
Área das Ciências Exatas e Ambientais
Docente: Daniele Simoneti
Comp. Curricular: Mecânica
Revisão G2
Força e Leis de Newton
Ex. O bloco B da figura pesa 600N. O coeficiente de atrito estático entre o
bloco e a mesa é 0,25. O ângulo θ é de 30º. Suponha que o trecho da corda
entre o bloco B e o nó é horizontal. Determine o peso máximo do bloco A para
qual o sistema permanece em repouso.
Ex. O corpo apoiado no plano inclinado representado na figura tem massa 30kg
e o coeficiente de atrito cinético entre ele e o plano é igual a 0,2. Qual é o
módulo da força que a pessoa deve exercer para que o corpo:
Suba o plano com velocidade constante?
Desça o plano com velocidade constante?
Suba o plano com aceleração de 0,5m/s2?
Ex. Um bloco de massa 5kg está deslizando com velocidade constante para
baixo sobre um plano inclinado que faz ângulo de 37o em relação à horizontal.
a) qual é o módulo da força de atrito?
b) qual é o módulo do coeficiente de atrito cinético?
Ex. Um bloco A, de massa 5 kg, está preso a outro B, de massa 3 kg, por meio
de uma mola ideal de constante elástica 800 N/m. Os blocos estão apoiados
sobre uma superfície horizontal e se movimentam devido à ação da força F
horizontal, de intensidade 64 N. Sendo o coeficiente de atrito cinético entre as
superfícies em contato igual a 0,4, determine a distensão da mola, em metros.
Momento de uma força (M)
Define-se momento de uma força (ou torque),
como a eficiência em realizar movimento de
rotação em torno de um eixo. Determinado a partir
de uma força F aplicada num ponto P de uma barra,
que pode girar livremente em torno de um ponto O
(denominado eixo de rotação).
M = Fd
Movimento sentido horário M < 0;
Movimento sentido anti-horário M > 0.
O efeito girante do torque depende de
duas coisas: da intensidade da força aplicada e
do comprimento do braço da força.
É importante perceber que o Torque
ou Momento de uma Força faz um
corpo girar. Para que um corpo NÃO
gire, a somatória dos Momentos deve
ser ZERO.
Condições de equilíbrio de um corpo extenso:
São duas as condições para que um corpo
extenso rígido esteja em equilíbrio:
•1a – Equilíbrio de translação A resultante do
sistema de forças deve ser nula → ΣF = 0
•2a – Equilíbrio de rotação A soma algébrica dos
momentos das forças que agem sobre o sistema,
em relação à qualquer ponto (eixo O), deve ser
nula → ΣM = 0
Ex.: Dois atletas estão sentados em lados
opostos de uma gangorra, como mostra a figura.
Determine o momento resultante em relação ao
eixo de rotação? Determine para que lado a
gangorra cairá?
Ex.: A barra AB da figura tem peso 1000N e está em
equilíbrio na horizontal, conforme indica a figura
abaixo. Sabendo que a deformação da mola é de
20cm e o peso da carga pendurada é 2250N,
determine:
a) a reação do apoio em A;
b) a constante elástica da mola.
Ex.: O sistema da figura está em equilíbrio e os
pesos da barra e das polias podem ser ignorados.
Determine a razão entre as massa M/m.
Ex.:A figura abaixo mostra uma barra homogênea de
peso 10 N e de comprimento 10 m que está apoiada
sobre um suporte distante de 3,0 m da sua
extremidade esquerda. Pendura-se um bloco de massa
m = 2,0kg na extremidade esquerda da barra e colocase um bloco de massa M = 4,0 kg sobre a barra do lado
direito ao suporte. Determine o valor de D, em metros,
para que a barra esteja em equilíbrio.
Trabalho
Dependendo do ângulo entre F e d, o trabalho
pode ser:
• Se 0o ≤ θ < 90o, o trabalho é positivo (trabalho
motor);
• Se 90o < θ ≤ 180o, o trabalho é negativo
(trabalho resistente);
• Se θ = 90o, o trabalho é nulo.
Potência
• Se uma força realiza um trabalho ∆T durante
um intervalo de tempo ∆t, a potência P, dessa
força é definida como sendo: P = ∆T / ∆t;
• Trabalho medido em J (joules);
• Tempo medido em s (segundos);
• Potência: 1J/s = 1 watt = 1W.
Energia Mecânica
Energia Cinética
Energia Potencial
Gravitacional
Elástica
Energia Cinética
• Associada a corpos em movimento;
• Depende da massa do corpo e do quadrado de
sua velocidade:K = (m v2)/2;
• Massa medida em quilogramas (kg);
• Velocidade medida em metros por segundo
(m/s);
• Energia Cinética medida em joules (J).
Energia Potencial Gravitacional
• Está associada à posição de um corpo no
campo gravitacional da Terra;
• Se um corpo de massa m encontra-se a uma
altura h acima de um nível referência, este
corpo possui uma energia expressa por:
Ug=mgh.
Energia Potencial Elástica
• Associada às deformações elásticas que os
corpos apresentam quando sofrem a ação de
forças de tração ou compressão.
• Ue = (kx2)/2, onde k é a constante elástica da
mola e x é a deformação sofrida pela mola.
Energia Mecânica
Energia Mecânica é a energia total de um sistema. Ela é
obtida através da soma das energias cinética e potencial
em um determinado ponto.
EMEC A = EP
EMEC A = EP
EMEC B = EC
EMEC B = Eel
EMEC C = EC + EP
Sistema Conservativo
Um sistema é conservativo quando não há dissipação
de energia mecânica, ou seja, transformação em outro
tipo de energia como térmica, sonora, luminosa, etc.
No sistema conservativo, a energia mecânica em cada
ponto é constante.
EMEC A = EC = 400J
EMEC B = EC + EP = 150 + 250 = 400J
Pode-se afirma que:
EMEC A = EMEC B
Movimento Circular
Ex. Nos trilhos de uma montanha-russa, um carrinho com seus ocupantes e
solto, a partir do repouso, de uma posição A situada a uma altura h, ganhando
velocidade e percorrendo um circulo vertical de raio R = 6,0 m, conforme mostra
a figura. A massa do carrinho com seus ocupantes e igual a 300 kg e desprezase a ação de forcas dissipativas sobre o conjunto. Determine a altura mínima h
que o carrinho deve iniciar o movimento para ter energia suficiente para atingir o
ponto B.
Ex. Um engenheiro deseja projetar uma pista curva para uma rodovia
interestadual de tal forma que um carro não tenha que depender do atrito para
fazer a curva sem deslizar. Suponha que um carro faça a curva com velocidade
de 15m/s e que o raio da curva seja de 50m, qual é o ângulo de inclinação que a
curva deve ter?
Quantidade de
movimento e Impulso
Quantidade de Movimento → Q
r
r
Q = m.v
Forma
vetorial
Q = m.v
Forma
escalar
Kg.m/s
kg
m/s
Q
v
Impulso de uma Força→I
r
r
I = ∆Q
I = ∆Q
Forma
vetorial
Forma
escalar
I = Q − Q0
I = m.v − m.v0
É a medida da variação da
quantidade de movimento de um
corpo.
Quantidade de
movimento e Colisões
A
vA
B
Fase de
aproximação
A
v'A
e → coeficiente de
restituição
(0≤ e ≤ 1)
vB
Fase de
afastamento
B
v'B
v AF
e=
v AP
vB '−v A '
e=
v A − vB
Tipo de Colisão
Perfeitamente
Inelástica
(e = 0) →saem
juntos
Parcialmente
Inelástica (ou
Elástica
(0 ≤ e ≤ 1)
Perfeitamente
Elástica
(e = 1)
Quantidade de
Movimento
Energia Cinética
Qi = Qf
Eci > Ecf
Qi = Qf
Qi = Qf
Eci > Ecf
Eci = Ecf
Em qualquer colisão temos:
Qi = Q f
m A .v A + mB .vB = m A .v A '+ mB .vB '
Nas inelásticas
m A .v A + mB .vB = (m A + mB ).v'
Saem juntos
Ex. A figura mostra uma esfera A que, partindo do repouso, desliza (sem rolar)
ao longo de uma rampa de altura H=20 m e a seguir ao longo de um plano
horizontal, ambos sem atrito. Num dado ponto do plano horizontal, a esfera A
se choca com uma esfera B de mesma massa, presa ao teto por um fio ideal.
Sendo esse choque parcialmente elástico com coeficiente de restituição e=0,4,
determine:
a) as velocidades de A e de B imediatamente após o choque;
b) a altura máxima h atingida pela esfera B após o choque com A.
Ex. Dois corpos A e B de massas iguais a 2 kg e 6 kg, respectivamente,
movimentam-se sobre uma mesma trajetória, sem atrito. Determine as
velocidades v'A e v'B após o choque. Considere uma colisão perfeitamente
elástica (e = 1).