Meteorologia Geral 2011 CAPITULO V MOVIMENTOS ATMOSFÉRICOS A causa fundamental dos movimentos atmosfericos é a diferença de Pressões entre duas regiões. O vento é resultado da acção de forças, das quais a força devida à pressão é a origem do movimento. A atmosfera age através do vento como uma resposta às diferenças de pressão, no sentido de diminuir essas diferenças. Assim é de esperar que o vento sopre no sentido das regiões de Pressão mais Alta para as de regiões mais Baixa. Figura 5.1: O Vento. 5.1 O Gradiente de Pressão Atmosférica Em princípio, para uma função tridimensional como a pressão atmosférica o gradiente é definido como: p ( x, y, z ) (p x)i (p y) j (p z )k Cláudio Paulo & Gilberto Mahumane Página 1 Meteorologia Geral 2011 Na prática esse vector dá a taxa de variação da pressão em função da distância, na direcção em que essa variação é máxima. Se, por exemplo, forem calculadas as components horizontais, a variação maior se dá na direcção perpendicular às isóbaras, como se vê na Figura 5.2. Figura 5.2: Gradiente de Pressão. O gradiente da pressão no ponto A da Figura 5.2 sera calculado por: p s p s 908 904 hPa 80km 4 hPa 80km 0, 05 hPa km 5 103 Pa m Note-se que no ponto B da Figura 5.2, embora a diferença de pressão seja a mesma, o espaçamento entre as linhas é maior. Substituindo na expressão: p s (908 904) hPa 120km 3,3 103 Pa m Cláudio Paulo & Gilberto Mahumane Página 2 Meteorologia Geral 2011 Ou seja, o gradiente de pressão é maior em regiões onde o espaçamento entre as isóbaras é menor, desde que a diferença de pressão entre duas isóbaras vizinhas seja sempre o mesmo. (No exemplo da Figura 5.2, elas estão espaçadas de 4 hPa). 5.2 Força Gradiente de Pressão Considere-se a Figura 5.3, de um element de volume de ar. Na direção x a parcela sofre a ação de forças devidas à pressão sobre as duas paredes opostas. Figura 5.3: Força de Gradiente de Pressão. Se na Parcela à esquerda a pressão é P , a força atuando da esquerda para direita é: Fx P A P y z A força atuando na parte direita, em sentido contrário, onde a pressão é P P P , é: Fx P y z ( P P) y z P y z A força por unidade de massa é então: Cláudio Paulo & Gilberto Mahumane Página 3 Meteorologia Geral 2011 f px Fpx M P y z v P. y z x y z (1 ) (P x) ou: f px (1 ) (P x) ou seja, a força gradiente de presão na direção x é proporcional ao gradiente de pressão nauqela direção. As expressões são análogas para as outras direções, então se pode escrever: f P (1 ) (P x)i (P y) j (P z )k (1 ) P A componente vertical da força gradiente de pressão é aproximadamente equilibrada pelo peso da parcela, razão pela qual na análise dos movimentos atmosféricos se calcula a força gradiente de pressão somente na horizontal: f PH (1 ) H P 1 (P x)i (P y)k ou, se se considerar, como no caso da Figura ao lado, a direção perpendicular às isóbaras: f PH (1 )(P S ) O sinal negativo da expressão indica que a força tem sentido oposto ao da variação positiva da pressão. Cláudio Paulo & Gilberto Mahumane Página 4 Meteorologia Geral 2011 O cálculo pode ser feito também em mapas de alturas geopotenciais para superfícies isobáricas. Na Figura 5.4, o segmento inclinado faz parte de uma superfície isobárica. Pode-se escrever: f PX 1 ( P P) x Ao mesmo tempo, usando a equação hidrostática entre os pontos B e C: P P g z ou P P g z Substituindo na equação da força gradiente de pressão: f Px (1 ) g z x Fazendo x, y 0 , f Px g z x onde z x é o gradiente de altura geopotencial para variação horizontal da distância. Cláudio Paulo & Gilberto Mahumane Página 5 Meteorologia Geral 2011 Figura 5.4: Força de Gradiente de Pressão. 5.3 Força de Coriolis A força de coriolis é uma força fictícia que aparece quando se observa o movimento da atmosfera a partir de um sistema de referência preso à Terra, devido à própria rotação da Terra. Para entender o seu significado, pode – se observar a Figura 5.5. Figura 5.5: Força de Coriolis. Suponha-se inicialmente que a Terra esteja girando e com ela arrastando o ar. Uma parcela sobre o Equador terá velocidade V R V onde é a velocidade angular da Cláudio Paulo & Gilberto Mahumane Página 6 Meteorologia Geral 2011 Terra e R é a distância entre o ponto na supeficie da Terra e o eixo de rotação. No caso, 7, 292 105 rd s e R 6.370km 6,370 106 m . Se uma força resultante agindo perpendicularmente à velocidade inicial levar esta parcela de ar até um ponto ao norte do Equador, a componente da velocidade paralela ao Equador não vai variar. Porém, distância da parcela ao eixo de rotação num ponto afastado do Equador é menor que a distância no Equador (na latitude de 30 N ela vale R R cos30 5,523 106 m ). Assim, a velocidade de um ponto preso à superfície da Terra naquela latitude será menor que um ponto preso ao Equador e portanto menor que a velocidade da parcela que veio do Equador até aquele ponto. Ou seja a parcela vai ter uma velocidade em relação à Terra na direcção oeste-leste para a direita. Como essa velocidade era nula quando a parcela estava no Equador, para um observador no solo parece-lhe que a parcela foi acelerada por uma força perpendicular à velocidade sul-norte. Se a parcela estivesse inicialmente parada num ponto acima do equador e fosse levada em direcção ao Equador, o desvio seria para oeste. Assim, no hemisfério norte a força de Coriolis, actua perpendicularmente ao movimento da parcela, apontando para o lado direito do movimento. No hemisfério sul ela actuaria em sentido oposto, isto é, para o lado esquerdo do movimento. Além disso, a força de Coriolis é proporcional à velocidade, é maxima nos polos e nula no Equador. Devido ao facto de a força de Coriolis ser perpendicular ao movimento, o trabalho realizado por ela é nulo, portanto ela só actua no sentido de mudar a direcção da velocidade e não alterá-la. Cláudio Paulo & Gilberto Mahumane Página 7 Meteorologia Geral 2011 5.4 Balanço Geostrófico Pode-se agora verificar o efeito das duas forças sobre uma parcela de ar. Seja, na Figura 5.6, a parcela inicialmente parada, porém sugeita à força gradiente de pressão f P . No início, como a velocidade é nula, a força de Coriolis também é nula. A força gradiente de pressão vai acelarar a particula e, à medida que a velocidade fôr aumentando, vai aumentando a força de Coriolis que vai desviando a partícula para a esquerda (no hemisfério sul). Essa força não altera a velocidade da parcela, mas esta será acelerada pela força gradiente de pressão e a força de Coriolis vai tornando a velocidade cada vez mais paralela às isóbaras e portanto a força de Coriolis se torna cada vez mais paralela à força gradiente de pressão e oposta a esta. No momento em que as duas forças se igualam, a força resultante é nula e a velocidade não vai mais variar, isto é, a força gradiente de pressão não vai mais acelerar a parcela. Esse equilíbrio é chamado “balanço geostrófico” e a velocidade correspondente é chamada “velocidade geostrófica”, indicada por Vg . Caso houvesse um súbito aumento da força gradiente de pressão, a parcela seria acelerada, aumentaria a força de Coriolis e se restabeleceria o equilíbrio. Figura 5.6: Balanço Geostrófico. Pode-se aqui estabelecer uma regra de que o movimento das parcelas em equilíbrio dinâmico se processa paralelamente às isóbaras, de forma que as baixas pressões se Cláudio Paulo & Gilberto Mahumane Página 8 Meteorologia Geral 2011 encontram à esquerda do movimento no hemisfério sul e à direita do movimento no hemisfério norte. No caso de isóbaras curvas, às forças gradiente de pressão e força de Coriolis deve-se acrescentar outra força fictícia que é a força centripeta, de forma que no equilíbrio a velocidade da parcela tangencie as isóbaras. No caso de isóbaras fechadas o movimento será em torno dos centros. No caso de centros de baixa pressão, o movimento será horário, e no caso de centros de alta pressão, no sentido anti-horário, ambos os casos no hemisfério sul. No hemisfério norte a regra é oposta. A seguinte regra mecânica é válida para o hemisfério sul: Tabela 1: Regra mecânica para o Hemisfério Sul. Hemisfério Sul Centro de pressão Alta Baixa Sentido do movimento Anti-Horario Horario Nome do sistema Anti-Ciclone Ciclone Cláudio Paulo & Gilberto Mahumane Página 9 Meteorologia Geral 2011 Figura 5.7: Balanço Geostrófico num sistema curvo. 5.5 Força de Atrito Suponha-se que a atmosfera seja dividida em camadas superpostas e que camadas adjacentes tenham velocidades médias diferentes. Neste caso diz-se que existe um cisalhamento vertical do vento. Cisalhamento é então definido como uma variação da intensidade do vento quando se desloca perpendicularmente a ele. Na verdade, cada camada é composta de moléculas com velocidades distribuidas caoticamente em todas as direcções e que em média resultam na velocidade do ar na camada. Como vai haver moléculas passando de uma camada para outra, as moléculas que passam da camada mais lenta para a camada mais rápida, vão em média diminuir a velocidade desta, e as que passam da camada mais rápida para a mais lenta vão em Cláudio Paulo & Gilberto Mahumane Página 10 Meteorologia Geral 2011 media aumentar a velocidade desta. Esse fenómeno se chama “transporte de momento na vertical”. O efeito macroscópico desse fenómeno é a variação do momento linear das camadas, que pode ser representado por uma força, chamada a “força de atrito” ( f a ). Como mostra a Figura 5.8, a força de atrito actua na camada mais rápida no sentido de diminuir a velocidade e, na camada mais lenta, no sentido de acelerá-la. No caso da camada adjacente à superficie da terra, a transferência de momento se dá entre a terra e a camada de ar, sendo que a terra tem momento zero e quando a camada de ar lhe transmite momento, a variação de velocidade da Terra é imperceptível. Em termos práticos, a força de atrito tem as seguintes características: Figura 5.8: Força de Atrito. a) É contrária ao movimento, isto é, actua em sentido contrário ao da velocidade. b) É proporcional à velocidade, c) É tanto maior quanto mais próximo da superfície da terra. Cláudio Paulo & Gilberto Mahumane Página 11 Meteorologia Geral 2011 O efeito das três forças (gradiente de pressão, Coriolis e atrito) está representado na Figura 5.9. Neste caso também se atinge um equilíbrioentre as forças. Note-se aqui que a velocidade tem uma componente perpendicular às isóbaras, no sentido das pressões mais altas para as pressões mais baixas. Em torno de centros de baixa pressão e de alta pressão, essa componente tem o sentido de entrar nos de baixa e sair dos de alta pressão. Figura 5.9: O Efeito das três forças (em cima) e o sentido da velocidade em torno dos centros de baixa e alta pressão. A força de atrito, sendo maior próximo da superfície, determina o cruzamento das isóbaras pelo vento, com muito mais eficiência para os níveis mais baixos da atmosfera. As duas Figuras abaixo (Figura 5.10 e 5.11) exemplificam esse facto. Na carta de superfície os ventos são mais fracos e cruzam as isóbaras. Na carta de 500 Cláudio Paulo & Gilberto Mahumane Página 12 Meteorologia Geral 2011 hPa , os ventos são mais fortes e paralelos às fortes e paralelos às isolinhas de altura geopotencial. Figura 5.10: Direcção do Vento. 5.6 Perfil Vertical do Vento Devido ao atrito do solo, o vento tem velocidade zero na superfície. O cisalhamento devido ao atrito, ou a variação vertical da velocidade horizontal do vento, depende da velocidade do vento e da rugosidade da superfície. Essa rugosidade pode ser provocada pela presença de plantas na superfície ou outros obstáculos, e o perfil vertical toma a forma: V k ln( z z0 ) onde k é uma constante aproximadamente igual a 1 e z0 é um parámetro de rugosidade que varia de 0,1cm para superfície de areia até cerca de 10cm para grama Cláudio Paulo & Gilberto Mahumane Página 13 Meteorologia Geral 2011 alta. Note-se na Figura 5.12 que, para plantas mais altas a velocidade junto ao solo é menor. Figura 5.12: Perfil vertical do vento. 5.7 Vento Térmico Outra causa do cisalhamento vertical do vento é o chamado “vento térmico”. O fenômeno pode ser visualizado na figura seguinte onde estão representadas algumas superficies isobáricas. Percebe-se que a atmosfera é mais quente no lado direito da Figura 5.13, onde a espessura da camada entre as superficies isobáricas é maior. Nota-se que a inclinação das superficies vai aumentando com a altura. Este facto faz com que a força gradiente de pressão na horizontal também aumente com a altura, pois ela é proporcional ao gradiente de pressão, a velocidadedo vento num nível superior P2 e num nível inferior P1 é chamada “vento térmico” e é proporcional ao gradiente horizontal de temperatura. Cláudio Paulo & Gilberto Mahumane Página 14 Meteorologia Geral 2011 Figura 5.13: Vento Térmico. 5.8 Movimentos na Vertical Como foi visto, as forças que actuam na atmosfera na vertical estão quase sempre em equilíbrio, ou seja, as acelerações na vertical são muito pequenas comparadas com as acelerações na horizontal. Em consequência disso, enquanto as velocidades na horizontal podem variar de zero 0 até 150 ou 200 m s , a velocidade vertical não ultrapassa algumas dezenas de cm s , excepto em condiçoes muito especiais, de topografia abrupta ou de convecção intensa. Os movimentos verticais geralmente acontecem associados a movimentos horizontais e, embora pequenos, são muito importantes para a determinação do tempo presente. Entre as causas da componente vertical do vento, temos a convergência e divergência, os efeitos orográficos, a convecção e a ascenção nas frentes. Cláudio Paulo & Gilberto Mahumane Página 15 Meteorologia Geral 2011 a) Convergência e divergência Ao se observer um cemtro de baixa pressão na superfície, percebe-se que o ar é forçado a se movimentar em direcção ao centro. Como o ar não pode se concentrar ali, ele é obrigado a subir (uma vez que não pode descer e penetrar no solo). Esse movimento do ar, de modo que ele entra numa região, é chamado de convergência, como ocorre no caso dos ciclones. Ocorre o contrário num centro de alta pressão na superfície, onde o ar é forçado a sair da região (divergência) e ser substituído por ar vindo das camadas superiors, constituindo um movimento vertical para baixo, também chamado de subsidência. A conservação da massa do ar exige que a circulação se complete, havendo novos centros de convergência e divergência na atmosfera superior, como na Figura 5.14. Figura 5.14: Convergência e divergência. Devido ao movimento vertical do ar, os centros de baixa pressão geralmente se associam a regiões de alta nebulosidade e precipitação e os centros de alta pressão a regiões de céu limpo. Cláudio Paulo & Gilberto Mahumane Página 16 Meteorologia Geral 2011 b) Efeitos orográficos Quando a barreira de uma montanha se opõe ao vento, este é obrigado a subir sobre ela. Por essa razão é comum que a face da montanha à montante (de onde o vento flui), seja mais nebulosa e chuvosa e a face à vazante seja mais seca e quente, pois a humidade já foi condensada e transformada em precipitação antes do ar atingir esta outra face da montanha. Figura 5.15: Efeito Orográfico. c) Convecção Como já foi visto no texto, a convecção ocorre em atmosferas instáveis. Ela pode, porém, ser iniciada pela convergência do vento ou por efeito orográfico, ou também pode ser inibida pela divergência ou pela subsidência do ar ao descer uma montanha. d) Ascenção nas frentes frias e quentes O ar frio que se forma nos pôlos, flui em direcção ao Equador, formando oque se chama a “frente polar”. Essa frente, quando encontra o ar quente proveniente das regiões de latitudes menores, determina regiões alternadas, umas em que o ar frio invade regiões de ar quente e outras em que o ar quente invade regiões de ar frio. As primeiras são limitadas pelas chamadas frentes frias e as outras pelas frentes quentes. Cláudio Paulo & Gilberto Mahumane Página 17 Meteorologia Geral 2011 Os perfis verticais das frentes frias e quentes são diferentes, como mostram as figuras. Como o ar quente é menos denso e oferece menor resistência ao avanço do ar frio, a superfície limite entre as duas massas de ar é quase vertical próximo ao solo.O ar quente é obrigado a subir abruptamente, devido ao avanço do ar frio e ali se formam nuvens e precipitação. No caso da frente quente, o ar frio oferece maior resistência ao avanço do ar quente, então este sobe suavemente sobre o ar frio. As nuvens e a precipitação ocorrem muito à frente da frente na superfície e a precipiteção é mais leve e contínua. Note-se que a escala vertical das figuras está exagerada, uma vez que é da ordem da altura da troposfera, isto é, aproximadamente 10km . Figura 5.15: Frentes. 5.9 Escalas de Circulação 5.9.1 A Célula de Hadley ou de circulação directa A circulação do ar se inicia geralmente com o aquecimento diferencial entre duas regiões vizinhas. É intuitivo que o aquecimento do ar na superfície pode provocar a Cláudio Paulo & Gilberto Mahumane Página 18 Meteorologia Geral 2011 convecção, o ar sobe e deve ser substituído por ar da vizinhança na superfície. Entretanto a Figura 5.16 ilustra como se inicia o movimento na horizontal. Figura 5.16: Célula de Hadley. Sejam duas colunas de ar próximas, com a mesma temperatura inicial. Ambas têm a mesma espessura. Se a coluna da direita fôr aquecida, sua espessura será aumentada e a pressão à altura original será aumentada. O gradiente horizontal de pressão assim criado é que vai produzir o movimento. Esse tipo de circulação é conhecido como circulação térmica directa, formando a célula de circulação directa ou célula de Hadley. 5.9.2 Circulação primária ou planetária Em 1735 Hadley concluíu que, pelo facto de a região equatorial ser fortemente aquecida, o ar ali deveria ser ascendente, formando assim uma célula de circulação directa descendente nos pôlos. O ar se moveria então, na superfície, dos pôlos para o equador e, na alta atmosfera, do Equador para os pôlos. Devido à força de Coriolis, o vento que sopra na direcção do Equador seria desviado para o oeste, resultando assim os ventos alíseoa das regiões tropicais. Cláudio Paulo & Gilberto Mahumane Página 19 Meteorologia Geral 2011 Figura 5.17: Circulação Planetária. Porém, Hadley não previu que a própria força de Coriolis iria acelerar o vento na alta atmosfera para o leste, de modo que a velocidade seria altíssima quando atingisse latitudes acima de 30 (a 30 a velocidade já teria aumentado 62 m s e a 45 teria aumentado 135m s ). Isso causaria um desequilíbrio dinâmico e por isso o ar seria obrigado a descer aproximadamente à latitude de 30 . Próximo aos pôlos se forma outra célula de circulação directa e entre as duas células há uma outra de circulação indirecta. Essa distribuição de ventos produz uma distribuição de climas sobre o globo terrestre: a cerca de 30 de latitude situam-se os desertos do mundo e a 45 50 , onde o ar é ascendente, está a faixa onde se encontra a frente polar, com suas frentes frias e quentes associadas. Cláudio Paulo & Gilberto Mahumane Página 20 Meteorologia Geral 2011 5.9.3 Circulação secundária ou sinótica É a circulação associada aos ciclones e anti-ciclones, e às frentes frias e quentes, com dimensões de uns poucos milhares de quilómetros. Como sabemos, a frente polar separa o ar frio dos polos do ar quente da zona temperada. Nessas duas regiões o vento sopra no sentido leste-oeste no ar frio e oeste–leste no ar quente. Figura 5.18: Frentes. O atrito entre as duas massas de ar se movendo em sentidos opostos produz uma ondulação na frente polar. A convergência dos ventos no vértice da ondulação produz um ciclone que se move com as frentes fria e quente no sentido oeste-leste. Note-se que a circulação em torno do ciclone transporta ar quente em direcção ao polo sul e ar frio em direcção ao equador. Isso quer dizer que o ciclone em latitudes médias, com suas frentes associadas, é um mecanismo de transporte de calor das regiões equatoriais para as regiões polares, que recebem menos energia solar. Cláudio Paulo & Gilberto Mahumane Página 21 Meteorologia Geral 2011 Figura 5.19: As Frentes e os Ciclones. 5.9.3.1 Ciclones tropicais Os ciclones tropicais ocorrem fora da frente polar, mais próximos do equador, em regiões de convergências de ventos sobre o mar, que vão se intensificar pela liberação de calor latente em nuvens de grande profundidade. Os ventos aí atingem velocidades altíssimas, que produzem desastres no mar e nas regiões costeiras. Uma vez que os ciclones tropicais entram terra adentro, perdem a fonte de energia que é a unidade evaporada do mar e decaem gradualmente até desaparecer. 5.9.3.2 Anti-ciclones Os anti-ciclones se formam em geral em regiões mais frias, de ar descendente ou entre dois ciclones. Em geral, no verão, a terra é mais quente que o mar, então se formam ciclones em terra e anti-ciclones nos mares adjacentes. 5.9.4 Circulação terceária São sistemas de ventos localizados com dimensões de ordem de 100km e curta duração. Cláudio Paulo & Gilberto Mahumane Página 22 Meteorologia Geral 2011 5.9.4.1 Brisa marítima e terrestre As brisas marítimas e terrestres são células de circulação directa do tipo de Hadley. No caso da brisa marítima, que ocorre durante o dia, a terra é aquecida pelo sol, e por sua vez aquece a atmosfera. O ar aquecido sobe e é substituído por ar mais frio do mar. Sobre o mar, então se formará um ramo de circulação descendente. O alcance da brisa marítima formada chega a 40 km terra adentro, e ela é responsável pelas chuvas à tarde. Note-se que o mar também recebe radiação durante o dia, porém se aquece menos que a terra. À noite, sem a fonte de energia solar, a terra se resfria mais rapidamente que o mar e a circulação é em sentido contrário, sendo chamada ”brisa terrestre”, que sopra da terra para o mar. Figura 5.20: Desenvolvimento da brisa marítima e terreste. Cláudio Paulo & Gilberto Mahumane Página 23 Meteorologia Geral 2011 5.9.4.2 Ventos de montanha e de vale Nos vales, devido ao aquecimento maior nas encostas, o ar é forçado a subir durante o dia. Por outro lado, à noite as encostas se resfriam mais rapidamente e o fluxo se inverte. Figura 5.21: Schematic illustration of flow in a valley: Left: in the early afternoon when the valley and upslope winds are occuring; Rigth: about midnigth when the floww is down the valley and the slope. Cláudio Paulo & Gilberto Mahumane Página 24
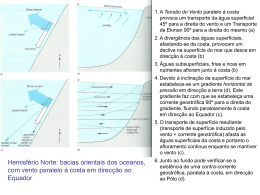
Baixar