PONTIFÍCIA UNIVERSIDADE CATÓLICA DE MINAS GERAIS
Programa de Pós-Graduação em Ensino de Ciências e Matemática
ESTRUTURAS ESTÁTICAS E SUAS RELAÇÕES CONCEITUAIS COM A
APRENDIZAGEM SIGNIFICATIVA:
Roteiro experimental para professores
Paulo Roberto Rodrigues Xavier
Maria Inês Martins
Belo Horizonte
2010
Sumário
Apresentação ........................................................................................................................ 3
1. Teoria da Aprendizagem Significativa .......................................................................... 4
2. Ensino da Estática e a Aprendizagem Significativa ...................................................... 7
3. Roteiros de Atividades Experimentais em Estática ........................................................9
APRESENTAÇÃO
Esse Roteiro é dirigido a professores de mecânica e estática, podendo ser trabalhado
em cursos de formação de professores de física, no ensino de engenharia e outros. O roteiro foi
criado para organizar a construção dos conhecimentos em estática, apoiada na prática
experimental e na computação, no trabalho grupal, na discussão e reconstrução desses
conhecimentos.
Assim o roteiro foi preparado para integrar às aulas de estática, uma discussão mais
ampla sobre estruturas, métodos simples de análise experimental, no sentido de mostrar uma
estática cada vez mais próxima da realidade dos educandos. As atividades propostas têm como
objetivo propor uma análise mais criteriosa, voltadas às aplicações em que os educandos são
levados a uma discussão mais profunda da mecânica aplicada.
E assim esperamos que a elaboração desse material possa enriquecer as aulas, com
mais uma possibilidade de planejamento, que envolve conteúdos pouco discutidos, mas que
representam em potencial grandes indicadores de aprendizagem.
1. TEORIA DA APRENDIZAGEM SIGNIFICATIVA
1.1 A teoria da aprendizagem significativa de David Ausubel
A teoria da aprendizagem significativa foi profundamente discutida pelo psicólogo
americano David Ausubel (1918-1997). Para Ausubel (1978) não basta reter informações, deve
haver uma organização cognitiva, onde informações se cruzam, se organizam e vão formando
novas estruturas de informações, que por sua vez são geradas relações entre uma nova informação
com outra armazenada anteriormente.
O aprendizado significativo acontece quando uma informação nova é adquirida mediante
um esforço deliberado por parte do aprendiz em ligar a informação nova com conceitos
ou proposições relevantes preexistentes em sua estrutura cognitiva. (Ausubel et al.,
1978, p. 159).
Para Ausubel, a aprendizagem é significativa quando novos conhecimentos ancoram-se a
conceitos relevantes e já existentes na estrutura cognitiva do aluno. Ausubel também define essa
estrutura como “ conteúdo total de ideias de um certo indivíduo e sua organização; ou conteúdo e
organização de suas ideias em sua área particular de conhecimentos”( Ausubel, 1978, p37-38).
Pretende-se então, recorrer a esses registros e interpretações para subsidiar conhecimentos
posteriores relativos à estática possibilitando ampliar a compreensão de seu campo de aplicação e
estimular a aprendizagem significativa. Segundo Ausubel (1978b, p.41), "a essência do processo
de aprendizagem significativa é que ideias simbolicamente expressas sejam relacionadas de
maneira substantiva (não literal) e não arbitrária ao que o aprendiz já sabe, ou seja, a algum
aspecto de sua estrutura cognitiva especificamente relevante para a aprendizagem dessas ideias.
Este aspecto especificamente relevante pode ser, por exemplo, uma imagem, um símbolo, um
conceito, uma proposição, já significativo". Para Ausubel (1978c) a aprendizagem pode ser
significativa ou mecânica. Já a aprendizagem mecânica, estabelece quando o novo conhecimento
se dá sem estar vinculado a estruturas cognitivas anteriores. Para isso, as novas estruturas devem
ser compatíveis com o nível de abstração, de compreensão do aluno.
Para Ausubel as informações na mente humana estão dispostas de forma altamente
organizada. Estas informações formam uma hierarquia conceitual onde os elementos mais
específicos de conhecimento são ligados e assimilados a conceitos mais gerais e inclusivos. Deste
modo, estrutura cognitiva significa uma estrutura hierárquica de conceitos, que são representações
resultantes de experiências sensoriais do indivíduo e do processamento mental da informação
recebida (Moreira, 1999).
1.2 Aprendizagem mecânica
Quando o indivíduo adquire uma nova informação com pouca ou nenhuma relação com
os subsunçores existentes em sua estrutura cognitiva, este conhecimento não se relaciona
subsunçores específicos e é armazenado de forma literal e arbitrária. Segundo Ausubel, apesar de
antagônica a aprendizagem significativa se relaciona mesmo localizando em posições opostas.
1.3 Subsunçores
Ao longo da vida de uma criança ocorrem diversos tipos de interações com a realidade,
em que vão se formando redes de conhecimentos em sua estrutura cognitiva. Contudo, essas
redes apresentam-se de forma aleatória, não correlacionando de forma lógica, mas esses
conhecimentos são utilizados para satisfação do próprio ego da criança. Para Ausubel (1978) a
criança adquire subsunções através do que chamou de processo de formação de conceitos, onde
ocorrem generalizações e são adquiridos por assimilação, diferenciação progressiva e
reconciliação integrativa.
Como mapear subsunções num individuo? Segundo Fialho (1996), só se pode
compreender um indivíduo a partir de toda sua história cognitiva. Ausubel também sugeriu o uso
de organizadores prévios como veículos facilitadores da aprendizagem significativa quando não
existem na estrutura cognitiva os subsunçores adequados. Os organizadores prévios são materiais
introdutórios apresentados em nível mais alto de abstração, inclusividade e generalidade antes do
material a ser aprendido em si. O papel desses facilitadores é formar uma ponte cognitiva entre as
ideias a serem ancoradas na estrutura cognitiva do estudante às novas informações.
1.4 Condições para a aprendizagem significativa
Ausubel propõe duas condições básicas para que ocorra a aprendizagem significativa:
1.4.1 Conceitos relacionáveis
As informações a serem assimiladas devem ser potencialmente significativas para o
aprendiz, ou seja, o estudante deve apresentar conceitos relacionáveis, de forma substantiva e não
arbitrária, vinculados diretamente com o conhecimento a ser aprendido, o qual, por sua vez, deve
ter significado lógico.
1.4.2 Potencialidade da informação
Para que uma informação seja potencialmente significativa, o aprendiz deve estar
disposto para aprendê-la, caso contrário esse modelo irá caracterizar uma aprendizagem mecânica.
Com isso, o material deve ser potencialmente significativo, para que o processo de
aprendizagem como um todo seja significativo.
Figura 1. Esquema da teoria de Ausubel.
Fonte: Arquivo pessoal.
O esquema acima revela a natureza da teoria da aprendizagem significativa de Ausubel.
O aluno que detém um conjunto de informações de forma não aleatória, em sua estrutura
cognitiva, acumula conhecimentos significativamente. Esse fato revela um caráter novo, não
muito discutido na teoria de Ausubel. Se a aprendizagem tem um histórico significativo, a
disposição do aluno deve ser diferenciada e, portanto as novas informações em potencial se
relacionam com maior eficiência aos subsunçores.
2. O ENSINO DE ESTÁTICA E A APRENDIZAGEM SIGNIFICATIVA
2.1 Estática e o Contexto
A Estática está localizada no eixo da Mecânica Newtoniana. Pode ser chamada também
de Isostática. A isostática funciona como um conjunto de conhecimentos prévios para as
disciplinas; Resistência dos Materiais, Teoria das Estruturas, Concreto, Estruturas de Aço,
Madeira e Projetos Estruturais.
A estática é sem dúvidas uma área da mecânica que antecede as disciplinas resistência dos
materiais e estruturas gerais, de máquinas, construções civis, metálicas e outras. Pois, abre
caminho para a compreensão de materiais e sua utilização no contexto e está intimamente
vinculada à realidade dos engenheiros, técnicos, profissionais de diversas áreas e o
desenvolvimento do conhecimento científico. A ciência a medida que evolui, fica presa ao
desenvolvimento de novas tecnologias para observação e análise de fenômenos. Por isso, essa
área de conhecimento liga teorias da mecânica aos grandes modelos práticos. Como isso se torna
uma das grandes áreas da física. Sem equacionar estaticamente uma estrutura, não podemos
prever que tipo de material a ser utilizado, logo, a compreensão dessa área se torna cada vez mais
importante, num mundo onde se busca cada vez mais materiais alternativos, técnicas de controle
e uso de materiais, reciclagem, economia, diminuição do peso de estruturas e vantagens
econômicas.
2.2 Estática e o Ensino
O ensino de estática não tem revelado o seu verdadeiro potencial de seus conhecimentos.
O pouco envolvimento prático, reduzido a quase zero têm proporcionado um desequilíbrio na
transmissão desses saberes. As aulas de estática, ao longo do ensino médio não revelam traços
marcantes na estrutura cognitiva de alunos e as vezes até esquecem ou agem como se nunca
tivessem ouvido falar em tais conhecimentos. No ensino médio há um conjunto fragmentado de
apresentações para o equilíbrio, sem relação com situações realísticas. Com isso temos uma área
de conhecimento prejudicada pela pouca divulgação de trabalhos e atividades experimentais que
envolvam professores e estudantes na reflexão e em seu enobrecimento. Para CARVALHO
(2004), os agentes envolvidos na disseminação de conhecimentos ao proporcionar,
um ensino que vise à aculturação científica deve ser tal que leve os estudantes a
construir o seu conteúdo conceitual participando do processo de construção e dando
oportunidade de aprenderem a argumentar e exercitar a razão, em vez de fornece-lhe
respostas definitivas ou impor-lhes seus próprios pontos de vista transmitindo uma visão
fechada das ciências. (CARVALHO, 2004, p.3).
Tem-se presenciado o pouco envolvimento por parte de educadores e estudantes na
evolução da transmissão dos conhecimentos ligados à estática. Conhecimentos fragmentados,
ausência de materiais de apoio, desvinculação com a realidade são condições que propiciam uma
visão obscura de saberes envolvidos na mecânica estática.
BIBLIOGRAFIA
AUSUBEL Ausubel, D., Novak, J., & Hanesian, H. Educational Psychology: A Cognitive View.
2.ed. New York: Holt, Rinehart & Winston, 1978.
AUSUBEL, David Paul. Aquisição e Retenção de Conhecimentos: uma Perspectiva Cognitiva,
Porto: Plátano Editora, 2003.
BEER, Ferdinand P., JOHNSTON JR., E. Russel. Resistência dos materiais. 3. ed. São Paulo:
Makron Books do Brasil, 1996.
BRASIL. Ministério de Educação. Secretaria de Ensino Fundamental Parâmetros Curriculares
Nacionais: matemática. Brasília: MEC/SEF, 1997.
D. Halliday, R. Resnick, J. Walker, Fundamentos de Física, v. 1, 4. ed., R i o d e J a n e i r o :
Livros técnicos e científicos, 1996.
F. P. Beer & E. R. Johnston Jr., Mecânica Vetorial para Engenheiros: Estática, v.1,
Makron.
J. L. Merian & L. G. Kraige, Mecânica - Estática: v.1. 5. e d. Rio de Janeiro: Livros
Técnicos e Científicos. 2006.
HIBBELER, R.C. Resistência dos Materiais, 3. ed. Rio de Janeiro Editora Livros Técnicos e
Científicos, 2000.
MOREIRA, Marco Antonio. Aprendizagem significativa: a teoria de David Ausubel. São Paulo:
Centauro, 2001.
R. C. Hibbeler, Estática: Mecânica para Engenharia, v. 1, Prentice Hall.
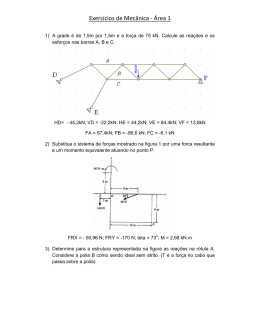
3. ROTEIROS DE ATIVIDADES EXPERIMENTAIS EM ESTÁTICA
3.1 Nome: Vetores e torres
3.1.2 Objetivos:
i) Determinar experimentalmente forças de tração e compressão através de coordenadas
conhecidas, em uma estrutura rígida, no equilíbrio estático.
ii) Aplicar conceitos de vetores no espaço tridimensional.
iii) Verificar experimentalmente e conceitualmente as linhas de ação das forças, reações normais
e momentos de uma força.
3.1.3 Materiais utilizados:
Quadro decimetrado, Cordonê ou cordinhas finas (que suporta até 5 kg), dois (02) dinamômetros
(de até 30N), Peso, aste ou barra rígida (torre), uma (01) balança, quatro massas de 1kg, cinco
(05) massas de 100 gramas e uma (01) massa de 0,5 kg (500g), quatro (04) roldanas com
prendedor ou parafusos.
3.1.4 Aplicações vetoriais e torres
As torres são estruturas que servem ao homem desde antigas culturas. Elas eram construídas em
posições geográficas estratégicas, em passagens fronteiriças e lugares de importância estratégica,
servindo de ponto de vigilância e gozava do prestígio popular. Há um provérbio chinês que diz:
"se um homem protege a passagem, dez mil não podem atravessá-la". Portanto vale lembrar que
eram necessárias essas estruturas dentro do contexto. As torres eram construídas de pedras e
atingiam grandes proporções em alturas e sustentação, permitindo que a sentinela pudesse ver
longe ser visto. Existiam torres comunicadoras em altas colinas, onde erram transmitidos sinais,
avisos, etc.
Figura 2. Torres de vigilância de Danba,
Figura 3. Ponte Pêncil – Japão. Aplicação
no sudoeste da China.
de sistemas cabos e torres.
Fonte: http://portuguese.cri.cn/101/2007 /
Fonte: http://aleosp2010.wordpress.
04/04/ 1@ 649 65.htm.
com/2008/10/ 06/ponte-pencil-japao/.
As torres de hoje são construídas para uso em telecomunicações, sustentando equipamentos de
transmissão de dados, redes elétricas, sustentando cabos de alta tensão, torres em pontes, torres
mistas, com vários fins.
As torres mais utilizadas atualmente, são as torres confeccionadas em metais como zinco, aço,
etc.
O princípio de manutenção do equilíbrio mecânico de uma torre está intimamente ligado aos
princípios da estática. A quantidade de forças que agem numa estrutura metálica deve ser zero
para que seja garantido o equilíbrio. Uma torre de sustentação de carga, por exemplo, recebe
alem de seu peso próprio, outras cargas externas, tais como vento, peso extra de equipamentos,
etc. Essas cargas são transformadas em trações e compressões na torre e comunicadas às barras
rígidas e levadas até o solo.
A figura 11 mostra uma torre, que consiste em uma treliça espacial rígida, disposta na vertical, e
apoiada em uma das extremidades sobre uma balança, ao longo do eixo z, enquanto três cabos
são conectados entre os pontos A, B, C e D.
No equilíbrio a soma das forças TCA , TDA e TBA sobre o ponto A se anulam. Portanto,
Forças existentes:
r
r
r
TBA TBAU1 TBAU BA
TBA( x )iˆ TBA( y ) ˆj TBA( z )kˆ ,
(tensão na direção AB)
r
r
ˆ
TCA TCAU 2 TCA( x )iˆ TC A( ) ˆj T A( z )k e
r
r
ˆ
ˆ
ˆ
TDA TDAU 3 TDA( x )i T DA( ) j T )k
(tensão na direção AC)
(tensão na direção AD)
RZ = peso na balança em k̂
(tensão na direção AO)
No equilíbrio o somatório das forças é nulo. Logo,
3
r
FA
r
0.
i 1
Podemos então analisar separadamente as forças em cada direção particular. Isto é,
3
r
F A( x ) TBA( x )iˆ TCA( x )iˆ
TDA( x ) iˆ
r
0
(forças atuantes na direção de x)
i 1
3
r
FA( y )
TBA( y ) ĵ TCA( y ) ĵ T DA( y ) ĵ
r
0
r
FA( Z )
TCA( z )k̂
r
RZ
(forças atuantes na direção de y)
i 1
4
TBA( z )k̂
TDA( z )k̂
r
0
(forças atuantes na direção de z)
i 1
No equilíbrio, os momentos, no ponto O em relação a cada força aplicada no ponto D são:
3
r r
ri Fi
r
0
i 1
r
rOD ( F1 x iˆ
r
r
F1 y ĵ F1 zkˆ) rOA (F2 x iˆ F2 y ĵ F2 zkˆ ) rOD (F3 x iˆ F3 y ĵ
r
F3z kˆ) 0
Quando as somas dos momentos se anulam, garante-se então o equilíbrio da torre?
3.1.5 Projetos Da Estrutura, Montagem e Procedimentos
A Montagem,
Consiste em um quadro decimetrado, ver figura 4, contendo indicações dos eixos, para ser
estabelecido um conjunto de coordenadas, três massas de pesos conhecidos (1 kg), e uma quarta
massa de peso variável (entre 1 e 3 kg variando a cada 100 gramas).
3.1.5.1 Prenda as roldanas em posições onde podem ser determinadas suas coordenadas em
relação aos eixos x e y (figuras 4 e 5). E coloque essas coordenadas na tabela abaixo (olhe por
cima da roldana e localize ou posicione na coordenada desejada). Dica: Coloque duas roldanas
de cada lado do quadro ou faça conforme a figura 6.
3.1.5.2 Amarre as massas no cordonê. Amarre as quatro extremidades dos corndonês e coloque
sobre as roldanas as respectivas massas. Coloque os valores das massas na tabela 1, a baixo,
3.1.5.3 Coloque um pequeno prumo (figura 7) para indicar as coordenadas do ponto O e insira
esse dado na tabela 1, a seguir;
Tabela 3.1.5.1. Dados Gerais da Montagem do Equilíbrio em um Plano
Roldanas
Pontos
A
B
C
D
Coordenadas
(
(
(
(
;
;
;
;
Massas (kg)
)
)
)
)
Coordenadas do
Trações
ponto central O
nos cabos
(dm)
O(
;
)
-------------------------------------------------------
(kgf)
AO
BO
CO
DO
Figura 4. Quatro tensões causadas por quatro
Figura 5. Quatro tensões causadas por quatro
pesos agindo sobre um ponto - vista 1.
pesos agindo sobre um ponto - vista 2.
Fonte: Arquivo pessoal.
Fonte: Arquivo pessoal.
Figura 6. Vista parcial da carga e um peso
Figura 7. Prumo colocado no ponto O, comum
agindo sobre causando trações e o equilíbrio.
aos cabos para verificação das forças.
Fonte: Arquivo pessoal.
Fonte: Arquivo pessoal.
Figura 7. Vista parcial da carga de um peso
Figura 8. Dois cabos tracionados e uma barra
variável agindo sobre uma roldana ( ponto A).
OC apoiada na origem sofrendo compressão.
Fonte: Arquivo pessoal.
Fonte: Arquivo pessoal.
3.1.6 Questionário
1) Quais devem ser os vetores, em notação de unitários, existente em cada cabo da figura 4 que
representam as tensões AO, BO, CO e DO?
2) O que ocorre com a soma das componentes desses vetores na direção de x? E de y?
3) O que acontece com o ponto O se aumentarmos a massa no ponto A (ver figura 5)? Justifique.
4) Tente deslocar o ponto O com utilizando a força das mãos. O que ocorrerá?
5) É possível encontrar as tensões que agem nos cabos mostrados na figura 8? Que dados devem
ser concedidos no problema? O que há em comum essa estrutura com a estrutura da figura 4?
Esse modelo pode justificar a construção de treliças espaciais? Explique.
6) Qual é o tipo de força sofrida pela barra, paralela ao eixo z, com extremidade na origem,
mostrado na figura 8?
7) Quantas forças são necessárias para produzir o equilíbrio no plano?
8) Se retirar uma das massas, ficando a montagem da figura 4 com apenas três tensões, será
possível o equilíbrio? Justifique a geometria do equilíbrio. É possível aplicar a lei dos senos para
resolver essa situação? Justifique?
3.1.7 Estudo de vetores e equilíbrio no espaço – tensões e torres.
3.1.7.1Apresentaçãodamontagem:
Figura 10. Torre apoiada em uma balança e sustentada por três cabos.
Fonte: Arquivo pessoal.
3.1.7.2 A montagem consiste em basicamente num quadro decimetrado, para que possam ser
visualizadas com certa facilidade as coordenadas onde serão aplicadas as tensões nas direções de
AB, AC e AD. A origem (base da torre) será considerada o ponto O (0,0,0). Esse ponto poderá
variar ao procurar o equilíbrio da torre na vertical. Já o ponto A deve está a uma altura Z. Note
que Z será a altura da treliça H mais a altura da balança H`,
portanto Z =H+H`. Veja as
dimensões da balança: 24cm x 17cm x 4cm.
3.1.7.3 A balança serve para apoiar a torre e medir a força de compressão devido às demais
tensões aplicadas aos cabos. O peso estrutura treliçada deve ser levado em consideração no
momento de achar a reação na balança. Para isso deve-se zerar a balança.
3.1.7.4 Os cabos servem para comunicar trações ao solo (quadro) e deverão ser conectados nas
posições sugeridas a seguir na tabela abaixo.
3.1.7.5 A massa M = 1 kg (podem ser sugeridos outras massas) deverá executar uma tensão e
comunicá-la a extremidade da barra que depois será comunicada as outras duas cordas.
3.1.7.6 Os dinamômetros podem ser colocados nos pontos de apoio C e D para medir as trações
nas duas cordas. Para que isso seja possível deverá existir um ponto de origem adequado, onde a
torre deverá ser deslocada até ficar equilibrada na vertical (em z).
Figura 11. Torre apoiada em uma balança e sustentada por cabos com a inserção de
dinamômetros D1 e D2.
Fonte: Arquivo pessoal.
3.1.7.7 Após montar a estrutura (figura 11), equilibrar as tensões, coloque os dados na tabela e
preencha os demais campos.
Tabela 3.1.7.1 Dados Gerais
Pontos
A
X
Y
UNITÁRIOS
U CA =
V
RES
TENSÕES(N)
T
TENSORES (N)
TCA =
C
U DA =
T
TDA =
D
U BA =
Dinamômetro
T
TBA =
Massa do bloco suspenso:
1:
N
Compressão na treliça em Dinamômetro2:
A:
N.
kg
Medida da balança:
N
r
VETOR rOA =
kg
3.1.7.1 Questionário
1) Qual é o tipo de força executada na direção axial da torre? Qual deve ser o valor dessa força?
2) Se os pontos A e C estiverem na mesma linha que contém o ponto O, é possível o equilíbrio?
Justifique.
3) Quais os valores de trações observados em cada um dos cabos?
4) Quais valores de cada tração nos cabos, encontrados através da análise teórica do equilíbrio?
5) Existe aproximação entre os valores práticos e os valores teóricos?
6) Quais os valores para cada momento? Mostre que há equilíbrio.
3.1.8 Conclusoes e Discussoes
3.1.7. Bibliografia
AMARAL, Otávio Campos. ESTRUTURAS ISOSTÁTICAS, 6. ed. Belo Horizonte: Eng e
Art, 1992.
BEER, Ferdinand P.; JOHNSTON JR., E. Russel. Resistência dos materiais. 3. ed. São Paulo:
Makron Books do Brasil, 1996.
CAMPANARI, Flavio Antônio. TEORIA DAS ESTRUTURAS. Rio de Janeiro: Guarnabara
Dois, 1985.
MASUERO E CREUS. INTRODUÇÃO À MECÂNICA ESTRUTURAL. Porto Alegre: Ed.
Universidade, 1997.
NASH, William A. Resistência dos materiais. 2. ed. São Paulo: McGraw-Hill, 1982.
NOGUEIRA, J.B. Mecânica dos solos: Ensaios de laboratório, São Carlos: EESC-USP, 1995.
FEIRA DE CIÊNCIAS. Sala 6, ESTÁTICA. Disponível em: http://www.feiradeciencias.com.br
/sala05/05_RE_08.asp, acesso em 30 de abril de 2010.
http://www.lese.upf.br, acesso em 16 de Abril de 2010.
ASSOCIAÇÃO BRASILEIRA DE CONSTRUÇÕES METÁLICAS. Siegbert Zanettini 50 Anos.
Ed 96/2010. Disponível em: www.abcem.org.br, acesso em 20 de Abril de 2010.
ESTRUTURAS METÁTICAS DE PEQUENO PORTE. F. A. LACERDA. 2004 http://estru
turasmetalicas.vilabol.uol.com.br/trelicas.htm, acesso em 26 de Abril de 2010.
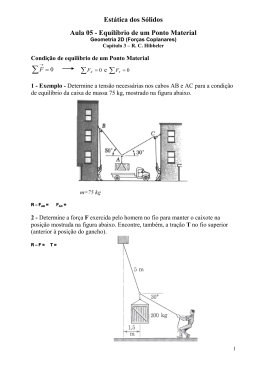
3.2 Distribuição de cargas
3.2.1 Nome: distribuição de cargas
3.2.2 Objetivos:
3.2.2.1 Verificar centro de massa e encontrar as reações de apoios, força cortante, momentos
através da análise do equilíbrio estático.
3.3.3 Materiais Utilizados:
02 balanças (carga mínima de 1,0 kg, precisão de 1 grama), pesos (de 1kg), placas de MDF em
diversos formatos de comprimento L= 80 cm e apoios.
3.4.4 Fundamentação Teórica - Histórico
O homem sempre esteve envolvido no processo das edificações, construindo muralhas, torres,
casas, pontes, palácios, etc. Essas construções além de serem úteis, transmitem ao longo dos
tempos, relações históricas, do homem e suas ansiedades, habilidades, a arte e a cultura. Para
garantir a sustentabilidade de uma edificação, os homens sempre procuram lidar com a força da
gravidade, utilizando técnicas de combinação de materiais e formas, chegando ao estágio da arte.
Para dominar conhecimentos e técnicas milenares vêm, ao longo da história, sendo desenvolvidas
metodologias cada vez mais eficazes. Os egípcios utilizam uma grande quantidade de
conhecimentos matemáticos em suas construções, contudo, os primeiros registros datam no
século XV, quando Leonardo da Vinci documentou testes de carregamentos e avaliação de
estruturas. Para BEER & JOHNSTON (1982), Galileu Foi um dos pioneiros do método empírico
aplicou testes de carregamentos, diferenciando também a tração simples da flexão, calculando
tensões em barras rígidas, “a resistência dos corpos sólidos é muito grande quando o esforço
solicitante é aplicado na direção longitudinal e muito pequena quando aplicada na transversal”.
Com a Revolução industrial, surge a necessidade de trabalhar a qualidade dos testes e os tipos de
materiais. Com isso surge a Mecânica Aplicada, com objetivo de conhecer materiais e suas
propriedades físicas. No século XIX, as construções eram realizadas com pequenos manuais de
resistência dos materiais envolvidos e havia grandes imprecisões nos cálculos. No século XX,
com demanda maior no setor habitacional, Leonhardt, na Alemanha realizou grandes quantidades
de ensaios e procedimentos experimentais propondo também Normas de Dimensionamento.
Atualmente existe no Brasil a NBR que define a utilização adequada de materiais conforme
carregamentos externos dentro de um padrão experimental pré-estabelecido. As cargas são
analisadas em condições de ensaios e utilização de métodos analíticos (que fica mais barato) e
tem-se um conjunto de informações sobre as cargas.
3.2.4.2DistribuiçãodeCargaseMomentodeInércia.
3.2.4.2.1 Vigas e cargas distribuídas
No cotidiano lidamos o tempo todo com conceitos e aplicações relacionados às cargas. As cargas
podem agir pontualmente, distribuída em linhas, em superfícies, em volumes, estar fixa ou
móvel, uniforme ou variável, agir sobre outros corpos, produzem aceleração, pode equilibrar e
desequilibrar um sistema de massas. Esses termos nos dizem respeito à preocupação que temos
em lidar com cargas. Na área de engenharia civil existe uma preocupação central; como organizar
de distribuir cargas de modo a dar sustentabilidade a uma estrutura. Para isso utilizam elementos
essenciais, tais como sapatas, pilares, vigas, lajes, coberturas e paredes que conceitualmente são
estruturas que relacional entre si, com outros modelos de cargas, na luta contra a gravidade, dos
ventos e fluidos.
A viga é um agente de significativa resistência que tem como objetivo suportar esforços externos
e comunicá-los em forma de trações e compressões até os apoios. Os esforços podem ser
externos, pontuais (agem em um único ponto) e distribuídos (agindo ao longo de um
comprimento, de uma superfície ou volume). Existe o esforço interno devido o peso próprio da
viga. Para entendermos o processo de distribuição das cargas é necessário entendermos, conceitos
de densidade linear, superficial e volumétrica de cargas, ou seja, a quantidade de carga por
unidade de comprimento, área e volume respectivamente.
Uma carga pode ser distribuída de forma linear, ou seja, quando a quantidade de massa envolvida
tem densidade observável apenas na maior dimensão (comprimento) da viga. Para isso
consideramos as demais dimensões com densidade constante e a quantidade de massa, também
constante. Sabendo então, a função da densidade da distribuição, pode ser determinada uma
massa total numa região R e com isso definir os centros de massas, reações nos apoios,
momentos de inércia, flexões, etc. Um exemplo de carregamentos está na figura 16, em que
uma viga está sujeita aos vários tipos de esforços, pontuais e distribuídos.
A figura 13 relaciona o carregamento da viga ao seu comprimento dxi que tem uma quantidade
de carga dM i . E a quantidade de carga total M será o somatório desses elementos dxi e dyi
numa região dAi onde, a carga total será a quantidade de carga por área
R {x1
x
x2 e y1
y
( x, y) na região
y2 } que abrange toda a viga, considerando a espessura (na direção
perpendicular a x e y) uniforme e igual a um, então
( x, y) 1 . Logo a massa total será,
y2 x2
n
M
lim
0
( x, y)dA
( xi , yi ) i A
i 1
R
dxdy ,
y 1 x1
x2
se a densidade linear (kg / m(SI )) for constante. Ou M
( x)dx
x , considerando apenas
x1
a distribuição da carga variando em relação à dimensão x. Simplificando essas funções temos,
M
L , onde L está na direção de x (ver figura 13). Para casos mais específicos, podem ser
estabelecidas as seguintes relações para cálculo das massas.
OBS: A integral da massa M coincide com a integral área quando é considerada a densidade da
distribuição superficial igual a um.
Massa numa Distribuição Linear de Cargas
B
M
( x)dx
R
( x)dx , onde R
{A
x
B} .
A
Massa numa Distribuição Superficial de Cargas
BD
M
( x, y)dA
R
( x, y)dydx onde R
AC
Massa numa Distribuição Volumétrica de Cargas
{A
x
B, C
y
D} .
B D F
M
( x, y, z)dV
( x, y, z)dzdydx onde R
{A
x
B, C
y
D, E
z
F}
AC E
Obs: ,
e
são as respectivas densidades de distribuições lineares, superficial e volumétrica
das cargas. A, B, C, D, E e F , são os limites nas integrais e podem representar funções.
3.2.4.2.2 Momento de inércia
O momento de inércia I é uma propriedade física, que mede a quantidade de massa (em kg ) a
uma posição r de um eixo de rotação. Numa definição geral, relaciona a densidade de
distribuição da carga M em uma área A localizada na posição r do eixo de giração. Num caso
mais genérico, podemos escrever que o momento de inércia será,
n
ri 2 M
I
i 1
Onde ri é à distância da partícula de massa M i ao eixo de rotação.
Para análise específica do momento de inércia em vários estilos de distribuição de carga,
considera a densidade
( x) medida em (kg / m) para uma distribuição linear,
em (kg / m 2 ) para distribuições superficiais e
( x, y) medida
( x, y, z) medida em (kg / m 3 ) nas distribuições
volumétricas. Essas densidades representam o comportamento da carga ao longo de suas
dimensões, definidas na região R e podem assumir valores constantes ou não. A soma desses
elementos de área, na região R , respectivamente, em cada elemento a cada elemento
distribuição continua linear,
i
A o elemento de área na distribuição superficial e
i
x na
V um dos i-
i
ésimos elementos de volume, respectivamente. Ao aproximar de zero, esses respectivos
elementos infinitesimais fornecem as seguintes relações:
Momento de inércia numa distribuição linear
n
i 1
Onde R {A
B
n
ri2 M i
I
x
( xi 2 ) ( x) i x
lim
0
i 1
( x 2 ) ( x)dx
R
( x 2 ) ( x)dx
A
B} numa distribuição linear de cargas entre pontos A e B na direção de x.
Momento de inércia numa distribuição superficial
n
B
n
ri2 M i
I
( xi 2
lim
0
i 1
yi 2 ) ( xi , yi ) i A
(x2
i 1
(x2
R
Onde dA dydx na região R
D
y 2 )dA
A
{A x
B, C
y 2 )dydx
C
y
D} .
( x2
y2
Momento de inércia numa distribuição volumétrica
n
n
ri 2 M i
I
( xi 2
lim
0
i 1
yi 2
zi 2 ) ( xi , yi , z i ) iV
i 1
z 2 )dV
R
BDF
( x2
y2
z 2 )dzdydx
AC E
Onde, dV
Para
dxdydz na região R
{A
x
B, C
y
D, E
z
F} .
( x, y)dA dM um elemento infinitesimal de massa, localizado numa região de área dA e
densidade ( x, y) medida em kg / m 2 .
3.2.4.2.3 Raio de Giração
Um sistema de pontos materiais define o raio de giração
, como uma grandeza física resultante
da razão entre o momento de inércia I pela quantidade de massa M .
I/M
Figura 12. Raio de giração de um sistema de massas. A equivalência dos momentos estáticos
e o raio de giração.
Fonte: Arquivo pessoal.
3.2.4.2.4 O teorema de Steiner
O teorema de Steiner ou teorema dos eixos paralelos é uma fórmula que nos permite calcular o
momento de inércia, de um sólido rígido, relativo a um eixo de rotação que passa por um ponto
O. Quando conhecemos o momento de inércia relativo a um eixo paralelo ao anterior e que passa
pelo centro de massas e a distância entre os eixos. O momento de inércia relativo ao eixo z é
verificado por,
Iz = ICM+Md2
Onde, I CM é o momento de inércia no centro de massa, M é a massa e d é a distância
perpendicular aos dois eixos.
3.2.4.2.5 Momento de inércia numa distribuição contínua de carga - vigas
Para calcular o momento de inércia de uma distribuição contínua de carga de massa M e
comprimento L relativo a um eixo axial a uma barra rígida que passa pelo centro de massa, devese recorrer à equação,
Onde numa direção onde a densidade ρ(x,y)=M/S é uma função da densidade superficial, ou seja,
a quantidade de massa M sobre uma área S , no plano xy . Para análise em uma única direção,
neste caso, em x , usa-se, I
x 2 dM onde dM é um elemento diferencial de massa que se
distribui ao longo do eixo das abscissas numa posição x , cuja densidade linear de carga é
M / L . Como
Como exemplo, o cálculo do momento de inércia na barra de comprimento L, cuja distribuição de
massa é constante, num ponto L/2 de seu comprimento.
Figura 13 – Cálculo do momento sobre uma barra rígida de comprimento L.
Fonte: Arquivo pessoal
A massa dM do elemento de comprimento da barra rígida compreendido entre x e x
dx é:
Logo, O momento de inércia da distribuição uniforme de carga será:
L/2
I
M 2
x dx
L
L/2
M x3
L 3
L/2
L/2
M
3L
L
2
3
L
2
3
M L
3L 8
3
L
8
3
ML2
12
3.2.4.2.6 Apoios
Para uma estrutura ser estaticamente determinada, os apoios devem obedecer as seguintes
condições:
i) Uma estrutura bi apoiada deve conter dois apoios sendo um móvel e outro fixo.
ii) O apoio móvel permite a ação dos esforços em apenas uma direção, impedindo translações.
Esse tipo de apoio pode agir em apenas uma direção. Exemplos: dobradiças, roletes e trilhos.
iii) O apoio fixo impede a existência de momentos e age em qualquer direção produzindo uma
reação que apresenta uma (01) ou mais componentes vetoriais.
Figura 14. Apoio fixo. A
Figura 15. Apoio móvel
Figura 16. Esquema dos
estrutura é parafusada no
com roletes. Existem
apoios utilizados na
furo.
outros formatos.
experimentação.
Fonte: Arquivo pessoal.
Fonte: Arquivo pessoal.
Fonte: Arquivo pessoal.
3.2.4.2.7 Forças Pontuais e distribuídas
As forças pontuais são forças que se concentram num único ponto. Seus efeitos são observados
na sua linha de ação. Na figura 17 podem ser observadas diversas forças pontuais. A
representação de uma força pontual é uma flecha indicando o módulo, a direção e o sentido da
grandeza.
Uma força distribuída não age apenas num ponto, pode agir ao longo de uma linha de carga
(viga), ao longo de uma superfície (lajes: forças agindo sobre uma área) ou sobre um volume (gás
dentro de um balão: tensão agindo numa região espacial), com isso deve ser representada por um
conjunto de várias fechas. Essas flechas também podem representar grandezas vetoriais, onde o
tamanho representa o módulo, e indicando a direção e o sentido. Existe um vetor normal à
superfície N que depende do plano.
Quanto aos comportamentos, uma força distribuída pode ser:
i) Uniforme - quando as uma força pontual ou distribuída apresenta linhas de mesmo tamanho,
mesma direção e sentido.
ii) Variável - quando a o carregamento pontual ou distribuído e assume valores diferenciados
quando se varia uma ou mais dimensões da estrutura.
Figura 17. Viga sujeita a um conjunto de cargas distintas.
Fonte: Arquivo pessoal.
3.2.4.2.8 Centro de Massa de uma Distribuição de cargas
Para cargas pontuais, considera-se para cálculo do centro de massa ( x , y ) as expressões:
Para distribuições de massas contínuas, temos, associamos a massa M aos momentos estáticos
M x e M y representados por: M x
yM e M x
xM . Considerando, a densidade do material
constante e igual a 1,
y
Mx
M
Mx
e x
Area
(x, y)
My
Area
xdA e M x
para M y
1
(M y , M x ) ou ainda ( x , y )
Area
3.2.5 Procedimentos experimentais:
3.2.5.1atividade1-Viga1
My
M
R
ydA .
R
1
(M y , M x )
Massa
A viga 1 tem um formato retangular e por isso a densidade da distribuição da carga é constante ao
longo de seu comprimento. Esta atividade pretende determinar grandezas tais como; o momento
de inércia em uma linha de carga (placa de MDF de (comprimento: 100 cm, altura: 10 cm x
espessura: 2 cm), de massa M), gerado por massas de 1 kg, localizadas nas posições mostradas na
tabela a seguir.
Figura 18. Viga 1 - Linha de carga contínua.
Fonte: Arquivo pessoal.
Tabela 3.2.5.1 Coordenadas onde são colocadas as massas de 1 kg.
Pontos
A
B
C
D
E
Abscissas
Ordenadas
Para calcular o momento de inércia do sistema relativo a um eixo perpendicular a linha de carga
deverá passar através de:
A) Um extremo.
B) Da segunda massa.
C) Do centro de massa.
3.2.5.1.1 Faça a seguinte montagem e calcule o momento de inércia relativo a um eixo
perpendicular a linha de carga e que passa pela primeira partícula, no ponto A.
Figura 19 – Momento de inércia em A onde uma barra está submetida a vários pesos.
Fonte: Arquivo pessoal.
3.2.5.1.2 Faça a seguinte montagem e calcule o momento de inércia a um ponto perpendicular a
linha de carga, que passa pela segunda partícula, no ponto B.
Figura 20 – Momento de inércia em B onde uma barra está submetida a vários pesos.
Fonte: Arquivo pessoal.
3.2.5.1.3 Faça a seguinte montagem e calcule o momento de inércia relativo a um eixo
perpendicular a linha de carga e que passa pela terceira partícula (centro de massas (em C)).
Figura 21 – Momento de inércia em uma barra rígida submetida a várias forças.
Fonte: Arquivo pessoal.
3.2.5 Questionário
1) Aplicando o teorema de Steiner, calcule o momento de inércia da distribuição de carga relativo
a um eixo perpendicular a mesma que passa por um de seus extremos.
2) Responda:
A) Em vez de calcular de forma direta os momentos de inércia, podemos calcular de forma
indireta empregando o teorema de Steiner?
B) Conhecido IC podemos calcular IA e IB, sabendo as distâncias entre os eixos paralelas
AC=0.5 m e BC=0.25 m?
C) A fórmula que temos que aplicar é I z
I
Md 2 ?
3) O que deve ocorrer se for alterado uma das coordenadas em y? Explique.
3.2.5.3 Atividade 2 – Vigas 2, 3 E 4.
3.2.5.3.1 Apresentação do projeto da montagem;
3.2.5.3.2 Estruturas: Os esquemas das montagens consistem, basicamente em apresentar vigas
com formatos diferentes, e colocados a cada vez sobre as balanças obtendo assim as reações nos
apoios, o centro de massa de cada estrutura, o momento e analisar as linhas de ações quando são
colocados pesos.
3.2.5.3.3 As balanças servem para apoiar a as vigas e medir assim a reação de apoio em cada lado
da estrutura.
3.2.5.3.4 Os diversos formatos das vigas servem para explorar conceitos de centro de massa,
integrais duplas aplicadas a centros de massa, momento de inércia, reações nos apoios e
momentos. Cada vértice das vigas apresenta um pequeno furo onde serão pendurado para
determinação experimental dos centros de massa, através da suspensão dos vértices e utilizando
um prumo. Para isso é necessário traçar linhas na viga suspensa por onde a linha do prumo passa.
No cruzamento das linhas está o centro de massa.
3.2.5.4VIGA2–Formatodefinidoporfunçõeslineares.
A viga 2 é definida por uma massa M na região R
{A
x
D, 0
y
f ( x)} . Como a função
na reta BC é uma reta, a f ( x) será a equação da reta que passa por estes pontos, considerando A
(0,0,0). Com isso o cálculo da massa envolver a densidade de distribuição de carga
seguinte relação.
Podendo também ser usado geometria básica para cálculo da massa.
( x, y) na
Figura 22. Viga 2 com densidade variável ao longo de seu comprimento.
Fonte: Arquivo pessoal.
As grandezas como massa M , centro de massa e o momento de Inércia I , são definidas por
geometria simplificada, quando se pode, ou usando o cálculo integral.
3.2.5.5VIGA3–Formatodefinidopormaisdeumafunção.
A viga 3 é definida por uma função que corresponde à massa M
contida na região
em que a f ( x) é uma reta que passa pelo
ponto C e pela coordenada f (G) , conforme a figura abaixo. As grandezas como massa M ,
centro de massa e o momento de Inércia I , são definidas por geometria simplificada, quando se
pode, ou usando o cálculo integral. Com isso o cálculo da massa envolver a densidade de
distribuição de carga ( x, y) constante na seguinte relação a seguir.
Figura 23. Viga 3 com densidade variável ao longo de seu comprimento.
Fonte: Arquivo pessoal.
As grandezas físicas podem ser encontradas seccionando a viga em duas regiões, definindo as
regiões R1 ={0<x<40; 0<y<30)} e R2={40<x<80; 0<y<f(x)}, onde f ( x) é a função da reta
decrescente que passa pelo ponto C, conforme a figura acima.
3.2.5.6VIGA4–Formatodefinidopormaisdeumafunçãoqualquer.
A Viga 3 tem um formato misto e poderá variar de acordo a necessidade estrutural. As grandezas
como massa M , centro de massa e o momento de Inércia I , são definidas pela resolução da
integral da região que define o formato da estrutura, utilizando o cálculo integral.
Figura 24. Viga definida por uma distribuição que varia conforme uma função.
Fonte: Arquivo pessoal.
As grandezas físicas podem ser encontradas fazendo o uso direto do cálculo integral onde a
massa da viga tem densidade constante em relação ao eixo z e varia em relação a x e y, logo a
região de integração será R={0<x<80; 0<y<f(x)} onde f(x) é a função que define a curva que
passa pelo ponto C, conforme a figura acima.
3.2.5.7PARTE2–Procedimentosparaencontraocentrodemassa
3.2.5.7.1 Pendure cada uma das vigas sobre o furo num suporte, conforme a figura.
3.2.5.7.2 Coloque uma linha de 100 cm amarrada sobre o suporte e na outra extremidade
coloque um pequeno peso (ver figura 26), marcando com um lápis ou pincel na madeira, uma
linha por onde passa o fio do prumo.
3.2.5.7.3 Após repetir 3.2.5.7.1 e 3.2.5.7.2 para cada furo, será determinado o centro de massa
cuja posição é o ponto de interseção das linhas desenhadas sobre a placa de madeira. Mostre
também que a linha divide a placa de madeira em partes iguais.
3.2.5.7.4 Verifique utilizando uma régua, a posição do centro de massa (x, y), colocando esses
dados na tabela 2.
Figura 25. Vigas 2 – Esquema das vistas frontal e lateral.
Fonte: Arquivo pessoal.
Figura 26. Verificação experimental do centro de massa.
Fonte: Arquivo pessoal.
3.2.5.7.5 Meça a massa de cada viga, a massa de cada apoio e anote esses dados na tabela 2;
3.2.5.7.6 Coloque as balanças a uma distancia de 100 cm. Coloque a viga 1 sobre as balanças, nos
dois apoios (figura 27) e verifique os pesos fornecidos pelas balanças e anote os dados na tabela
2.
3.2.5.7.7 Anote os dados referentes aos pesos mostrados nas balanças.
Figura 27. Viga 1 sobre duas balanças.
Fonte: Arquivo pessoal.
Tabela 3.2.5.2 Dados experimentais e teóricos.
Vigas
Massas (kg)
Prática Teórica
Viga 1
Viga 2
Viga 3
Apoio 1
Apoio 2
-------------
Centro de Massa
Prática
Teórica
(
,
) (
,
)
(
,
) (
,
)
(
,
) (
,
)
-------------------------
Peso na balanças (kg)
Balança 1
Balança 2
-------------
-------------
3.2.5.8 Questionário
1) Qual é o tipo de força executada pela balança? Qual deve ser o valor do peso de cada balança
quando a distribuição de massa é contínua? Por que isso ocorre?
2) Se adicionarmos pesos extras a viga 1, no ponto G, o que deve ocorre com as reações em D?
Qual deve ser o valor dessa massa para equilibrar as reações nas balanças?
3) Qual uma função que representa a distribuição da carga para as vigas 1 e 2?
4) Quais valores para os centros de massa de cada viga, utilizando o cálculo integral e diferencial.
5) Existe aproximação entre os valores práticos e os valores teóricos?
6) Qual o momento de inércia na viga 1? Mostre que há equilíbrio.
3.2.5.8.1Atividadedeverificaçãodaaprendizagem
Uma barra de 3 m de comprimento e pesando 400N, tem densidade linear constante e está
apoiada nas extremidades suportando duas cargas, de 40 N e 60 N, situadas a 1 m de cada
extremidade, conforme a figura. Determine: a) as reações nos apoios, b) o momento causado pelo
peso da barra sobre o ponto A, c) e faça o diagrama das flechas para as cargas atuantes e o
momento ao longo da barra.
Figura 28. Viga sobre duas balanças.
Fonte: Arquivo pessoal.
3.2.5.8.2Atividadedeverificaçãodaaprendizagem
A figura abaixo mostra uma viga de aço no formato I, de 7 m, sustentando uma carga variável.
Determine as reações nos suportes A e B para que a viga esteja em equilíbrio.
Figura 29. Viga no formato de I sofrendo um carregamento variável.
Fonte: Arquivo pessoal.
3.2.5.9ConfecçãodaViga3-FunçãodoCortenaMadeira
Viga 1: consiste numa placa de madeira MDF de dimensões: espessura = 2,3 cm , comprimento
= 100 cm e altura = 10 cm).
Utilizado uma chapa de madeira (MDF) de dimensões iniciais conhecidas (espessura = 2,3 cm ,
comprimento = 80cm e altura = 30 cm).
i) Obtenha a massa dessa chapa para conhecer a densidade
(massa por unidade de área)
3 2
ii) Conhecida a função f ( x) 3 10 x 10 que delimita a chapa, criar uma tabela onde se
obtém um conjunto dos pontos por onde passa o corte superior;
Tabela 3.2.5.3 Dados Gerados pela Função de Corte Superior da Madeira
x
y
5
10
15
20
25
30
35
40
45
50
55
60
65
70
75
10,0 10,3 10,6 11,2 11,8 12,7 13,6 14,8 16,0 17,5 19,0 20,8 22,6 24,7 26,8
iii) Depois de cortadas as peça (VIGA 1, VIGA 2 e VIGA 3). Verifique a massas e coloque seus
valores na tabela 1. Através da geometria, crie uma forma de verificar o valor aproximado da área
frontal da chapa. Utilize integração para encontrar o valor dessa área e compare os dados
experimentais com os dados teóricos. Discuta o método com os colegas.
iv) Faça pequenos furos nos vértices das chapas para que possam ser encontrados os centros de
massa numa análise da linha de ação pela força peso.
Figura 30.a. Placa de madeira apresentando a curva do corte.
Fonte: Arquivo pessoal.
Figura 30.b. Placa de madeira cortada.
Fonte: Arquivo pessoal.
3.2.6 Conclusoes e discussoes
3.2.7 Bibliografia – Distribuição de cargas
AMARAL, Otávio Campos. ESTRUTURAS ISOSTÁTICAS. 6. ed. Belo Horizonte: Eng e
Art, 1992.
CAMPANARI, Flavio A. TEORIA DAS ESTRUTURAS. Rio de Janeiro: Guarnabara Dois,
1985.
BEER, Ferdinand P., JOHNSTON JR., E. Russel. Resistência dos materiais. 3.ed. São Paulo:
Makron Books do Brasil, 1996.
MASUERO E CREUS, INTRODUÇÃO À MECÂNICA ESTRUTURAL. UFRGS: Ed.
Universidade, 1997.
MERIAN, J. ESTÁTICA. Rio de Janeiro: LTC, 1995
NASH, William A. Resistência dos materiais. 2.ed. São Paulo: McGraw-Hill, 1982.
NOGUEIRA, J.B. Mecânica dos solos: Ensaios de laboratório, São Carlos: EESC-USP, 1995.
WINKIPÉDIA, A ENCICLOPÉDIA LIVRE. O TEOREMA DE STEINER. 2010. Disponível
em:http://pt.wikipedia.org/wiki/ Teorema_de_Steiner, acesso em 21 de abril de 2010.
FEIRA DE CIÊNCIAS. Sala 6, ESTÁTICA. Disponível em: http://www.feiradeciencias.com.br
/sala05/05_RE_08.asp, acesso em 30 de abril de 2010.
CENTRO UNIVERSITÁRIO DE MARINGÁ. ANÁLISE DA FLEXIBILIDADE DE
DIFERENTES MATERIAIS UTILIZADOS NA CONFECÇÃO DE RETENTORES PARA
PPR2. 2005. Disponível em: http://www.cesumar.br/pesquisa/periodicos/index.php/iccesu
mar/article/viewFile/104/ 319 , acesso em 07 de maio de 2010.
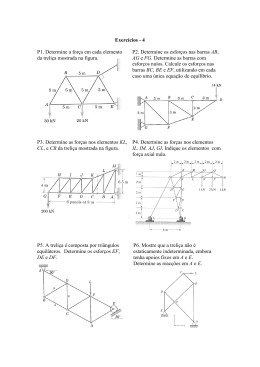
3.3 Treliças - Estruturas Reticuladas
3.3.1 Nome: estruturas reticuladas
3.3.2 Objetivos:
I. Determinar experimentalmente as forças de tração e compressão em treliças.
II. Determinar experimentalmente as reações nos apoios com aplicação de cargas externas.
III. Analisar e relacionar teoricamente as forças e momentos no equilíbrio estático.
3.3.3 Materiais Utilizados:
02 balanças (capacidade: 10 kg) , 02 pesos 1 kg, treliça com pseudo anéis isométrica de lados
L=50cm com pontos A, B, C, D e E.
3.3.4 Fundamentação Teórica
3.3.4.1Estruturastriangulares
São denominadas treliças as estruturas triangulares, formadas a partir de barras (cilíndricas,
retangulares, cantoneiras, etc.) rígidas (os efeitos das deformações são desconsiderados na análise
do equilíbrio), conectadas (por pinos, rebites, soldas, parafusos) em pontos denominados nós,
dispostas num plano geométrico (treliças planas) ou em mais de dois planos (treliças espaciais).
Figura 31. Nó ou
Figura 32. Torres.
Figura 33. Ponte cabos.
conectores de treliças.
Fonte:
Fonte: http://downloads
Fonte: Moiola e Malite.
http://2.bp.blogspot.com/
.open4group.com
Segundo Porto (2005) as treliças surgiram em meados do século XIX, com o escocês, Alexandre
Graham Bell (1847-1922) que criou a primeira estrutura metálica em formato tetraédrico. A partir
do século XIV, com a com a utilização do ferro fundido em construções, as treliças receberam
um grande espaço no campo das estruturas, adquirindo novos formatos e novas composições
materiais. Atualmente as estruturas triangulares são feitas a partir de qualquer material rígido que
suporte esforços de tração em compressão e servem para alternar o uso das vigas de concreto
armado. Portanto se fazem presentes nas grandes edificações, viadutos, pontes, torres, coberturas
e guindastes. Essas estruturas apresentam múltiplas vantagens, pois são leves, econômicas,
apresentam melhor desempenho e rapidez na montagem, vencem maiores vãos, suportando
maiores cargas, resistem a grandes trações enquanto concreto armado apresenta alta resistência à
compressão e baixa resistência à tração além de seu peso próprio ser grande em relação às
treliças. Contudo, em uma treliça não se pode aplicar forças em qualquer ponto, como acontece
com as vigas. Nas treliças as forças devem ser aplicadas nos nós, onde deverá ocorrer a
distribuição dessa força às demais barras conectadas ao referido nó. Essas forças vão percorrendo
às demais barras, se somando até chegar aos apoios. A figura 31 mostra um nó, onde há uma
concentração forças em diversas direções. A figura 32 mostra a beleza das torres de transmissão
de energia elétrica, uma das grandes aplicações de estruturas triangulares. Já a figura 33 mostra
uma ponte móvel (estrutura central) que pode ser deslocada na vertical para passagem de navios
entre os pilares centrais.
3.3.4.2TreliçasPlanas
Uma treliça é plana quando todos os pontos (nós), denominado aqui de elemento básico que estão
em um único plano e obedece a leis de formação, ou seja, relações simples entre a quantidade de
reações em cada nó R , o número de barras N e o número de nós n . Vejamos as relações básicas
que revelam a estaticidade das treliças:
i) N
ii) N
R
2n
Relação entre número das barras, número das reações e número dos nós.
2n 3
Relação entre o número de barras e o número de nós (treliça isostática).
Figura 34. Treliça plana – formação dos módulos planos a partir de um elemento básico.
Fonte: Arquivo pessoal.
Se N
2n 3 ou R N
2n , temos uma estrutura hiperestática, ou seja, haverá um número de
tensões superior ao esperado e, portanto haverá um conjunto indeterminado de variáveis. Mas se
N
2n
3 ou R
N
2n então a estrutura será hipoestática, ou seja, o número de barras não
poderá gerar o equilíbrio da estrutura.
iii) As forças externas devem sobre cada nó evitando efeito de flexão.
iv) cada triângulo deve conter no máximo duas forças de mesma natureza. Isto é, duas trações e
uma compressão ou duas compressões e uma tração.
Figura 35. Treliça plana.
Figura 36. Treliça plana de garrafa pet.
Fonte: www.fec.unicamp.br/.../ teoria /
Fonte: Arquivo pessoal.
estrutur/4.htm.
3.3.4.3TreliçasEspaciais
Segundo Silva (1999, p. 1), “as estruturas espaciais são aquelas compostas de malhas planas ou
curvas, tridimensionais, interligadas por elementos estruturais chamados barras ou membros,
conectados entre si por intermédio de peças ou dispositivos especiais, chamados juntas ou nós”.
As treliças tridimensionais são formadas a partir de quatro nós e seis barras rígidas, aqui
denominado de elemento básico. Na adição de cada nó, são adicionadas três novas barras e assim
sucessivamente. As treliças espaciais apresentam as vantagens apresentadas acima e suportam
maiores cargas. O elemento básico da treliça apresenta quatro planos e pode ter maior resistência
quando as barras são isométricas (quando as barras apresentam mesmas secções retas, mesmo
comprimento e mesmas propriedades físicas; resistência a tração e compressão, mesmo módulo
de elasticidade e mesma taxa de escoamento).
Numa treliça espacial, o número de barras N e a quantidade dos nós n serão relacionados por,
N
3n 6 .
Figura 37. Elemento básico de uma treliça espacial – Adição de nós e barras.
Fonte: Arquivo pessoal.
Figura 38. Treliça espacial construída
Figura 39. Treliça espacial. Aplicações de
por alunos – modelo: pé de galinha.
estruturas espaciais.
Fonte: Arquivo pessoal.
Fonte: Arquivo pessoal.
3.3.4.4Traçãoe Compressão.
As tensões nas barras são forças axiais (que agem na direção da maior dimensão da barra)
podendo ser de tração ou compressão. As trações agem impedindo o distanciamento dos dois
pontos onde está conectada. As compressões agem impedindo a aproximação dos dois pontos
onde é conectada.
OBS: Quando é construído o diagrama de corpo livre (DCL), as trações e compressões utilizadas
devem ser as forças executadas pela barra (vermelho) e não a força executada na barra (preto).
Figura 40. Tração e compressão em uma barra rígida.
Fonte: Arquivo pessoal.
3.3.4.5Determinaçãodastensões
Como pode ser visto na figura acima, as tensões axiais, trações e compressões, agem na direção
da barra e transmitem o módulo dessas forças até os pontos extremos. Quando se conhece
propriedades físicas de um material, pode-se conhecer a tensão aplicada ao corpo, através da
deformação. Pela Lei de Hook, E , em que é a força por unidade de área, é a deformação unitária,
(grandeza adimensional) sofrida pela barra e E é denominado módulo de Young. É importante
lembrar que essas deformações aqui salientadas devem ocorrer apenas na direção axial da
barra. Caso ocorra flexão, deve-se recorrer as equações diferenciais, fazendo analogia com cabos
e catenárias. A tensão ao longo de uma catenária tem módulo constante e varia em direção,
portanto faz-se uso de um vetor unitário direcional para determinar a tensão transmitida. Com isso
não será interessante e viável apresentar nesse momento tais expressões.
3.3.4.6Momentodeinércianasbarras
Genericamente, o momento de inércia I é:
n
ri 2 mi
I
i 1
Onde ri é a distância da partícula de massa mi ao eixo de rotação.
3.3.4.7CentrodemassadeumaTreliçaPlana.
As coordenadas do ponto ( x , y ) representam o centro de massa. Para chegar a seus valores é
necessário conhecer o ponto ( xi , yi ) de cada elemento da treliça de massa mi .
n
CM
( x , y ) encontrado por x
n
xi mi /
i 1
n
mi e y
i 1
n
mi .
yi mi /
i 1
i 1
3.3.4.8Análisedoequilíbrio
No equilíbrio a soma das forças e momentos deve ser nula. Daí deve-se escolhe um dos métodos
abaixo para solucionar o conjunto de esforços e reações existentes.
r
As equações do equilíbrio estático: M
n
r r
ri Fi
0
e
i 1
r
F
n
r
Fi
0
i 1
3.3.4.9MétododosNósouMétododeCremona Consiste
em verificar o equilíbrio de cada nó da treliça: i)
Determinação das reações de apoio.
ii) Identificação do tipo de tensão em cada barra (tração T ou compressão C),
iii) Fazer o diagrama de corpo livre e verificar o equilíbrio de cada nó da treliça, iniciando-se
sempre a análise a partir do nó que tenha o menor número de tensões desconhecidas.
3.3.4.10MétododeRitterouMétododasSecções i)
Secciona-se a estrutura em duas partes.
ii) Escolha uma região da treliça que apresente no máximo três tensões, para gerar um sistema
determinado e proceda a análise das forças e momentos, aplicando o diagrama de corpo livre
(DCL).
iii) Escolha uma região vizinha à primeira secção, onde se tem uma tensão conhecida (encontrada
em ii) e faça novo corte para verificação das forças. Repita esse procedimento até finalizar toda
estrutura.
3.3.5 Procedimentos Experimentais:
3.3.5.1Atividade1-Treliças
Estruturas propostas por alunos ao longo do curso de estática:
Figura 41. Treliça com pseudo anéis.
Figura 42. Torre feita em treliças planas.
Fonte: Arquivo pessoal.
Fonte: Arquivo pessoal.
3.3.5.2Formatos
As treliças mostradas nas figuras 45 a 50 representam a treliça da figura 41, feita em barras de
madeira de dimensões (1,5 cm x 1,5 cm x 50 cm) (ver montagem em 4.3.5.9). No ponto médio
de cada barra é colocado um anel de PVC (tubo PVCE de 75 mm) com largura de 1,5 cm. Esse
anel tem a função de indicar se a barra sofre tração ou compressão.
Figura 43. Barra de madeira com
Figura 44. Barra de madeira com pseudo anel
pseudo anel em compressão.
sofrendo uma força de tração.
Fonte: Arquivo pessoal.
Fonte: Arquivo pessoal.
3.3.5.3 Conforme a figura 46 e apoie a treliça nos pontos A e E. Coloque as massas de 1 kg*
sobre o ponto C e observe em cada pseudo anel o comportamento de barra e coloque na tabela se
é tração (T) ou compressão (C).
Figura 45. Treliça plana – dimensões.
Figura 46. Treliça. Apoios em C e E.
Fonte: Arquivo pessoal.
Fonte: Arquivo pessoal.
Tabela 3.3.5.1 Dados das Trações entre os Pontos A e E
Barras
Tipo de tensão
AB
AC
BC
BD
CD
CE
DE
*(pode ser acrescida para gerar melhor visualização nas deformações da treliça.)
3.3.5.4 Conforme a figura 46, apóie a treliça nos pontos C e E. Coloque uma massa de 2 kg (+/-)
sobre o ponto A e observe em cada pseudo anel o comportamento de barra e coloque na tabela se
é tração (T) ou compressão (C).
Tabela 3.3.5.2 Dados das Trações entre os Pontos C e E
Barras
Tipo de tensão
AB
AC
BC
BD
CD
CE
DE
3.3.5.5 Conforme a figura 17 e apóie a treliça nos pontos A e E. Coloque uma massa de 2 kg
sobre o ponto B e observe em cada pseudo anel o comportamento de barra e coloque na tabela se
é tração (T) ou compressão (C).
Figura 47. Treliça plana A – montagem 2.
Figura 48. Treliça plana A – montagem 3.
Fonte: Arquivo pessoal.
Fonte: Arquivo pessoal.
Tabela 3.3.5.3 Tipos de Tensões
Barras
Tipo de tensão
AB
AC
BC
BD
CD
CE
DE
3.3.5.6 Conforme a figura 48 e apóie a treliça nos pontos A e E. Coloque uma massa de 2 kg
sobre o ponto C e observe em cada pseudo anel o comportamento de barra e coloque na tabela se
é tração (T) ou compressão (C).
Tabela 3.3.5.4 Dados das Trações entre A e E
Barras
Tipo de tensão
AB
AC
BC
BD
CD
CE
DE
Figura 49. Treliça plana A – montagem 4.
Figura 50. Treliça plana A – montagem 5.
Fonte: Arquivo pessoal.
Fonte: Arquivo pessoal.
Tabela 3.3.5.5 Dados da Treliça para Cálculo do Centro de Massa
Barras
Massa (kg)
CM
(cm)
AB
( ;
AC
)
(
;
BC
)
(
;
BD
)
(
;
CD
)
(
;
CE
)
(
;
DE
)
(
;
)
4.3.5.7 Meça a massa de cada barra, na figura 45 (ou pese a treliças e divida seu peso pelo
numero de barras, desconsiderando o peso dos nós), e coloque na tabela abaixo as coordenadas
dos centros de massa (CM) de cada barra da treliça. (responda a questão 9).
3.3.5.8 A figura 51 mostra uma torre feita de madeira. Duas das laterais paralelas são feitas de
treliças planas (de palitos de picolé) e as outras duas laterais apresentam apenas barras (palito de
picolé) conectadas na horizontal, formando quadrados.
Aplique duas forças nas laterais
superiores da torre e verifique o comportamento. Discuta com os colegas suas conclusões.
Figura 51. Ação de forças horizontais em estruturas. Uma simulação forças laterais.
Fonte: Arquivo pessoal.
3.3.6 Questionários
1) Ao Aplicar as cargas nos pontos mencionadas nos procedimentos 4.3.5.3 ao 4.3.5.6 alguma
das barras modificou o comportamento das tensões? Quais? Tente explicar o que acontece.
2) Em qual (is) situação (ões) as reações nos apoios são iguais? Por quê?
3) Quais situações o apoio A executará maior reação que o apoio E? Justifique.
4) Observando o formato dos anéis, faça o diagrama de corpo livre para cada ponto da treliça
para a montagem representada pela figura 46.
5) Sabendo que cada barra da treliça é igual a 50 cm, calcule as reações em cada apoio na
montagem representada pela figura 46.
6) Coloque as massas, conforme a figura 49 e verifique os valores mostrados pela balança. Que
conclusões pode-se ter em relação à questão anterior?
7) O que deve ocorrer se for colocado uma massa de 1 kg (ou mais) em um dos anéis, conforme a
figura 50? Esse procedimento é correto? Justifique.
8) Mostre no diagrama de corpo livre que quando há dois apoios fixos a estruturas se torna
estaticamente indeterminável.
9) Onde deve está o centro de massa da treliça? Anote os dados na tabela 5. Considerações: o
comprimento de cada barra é de 50 cm e o ponto A está na origem.
10) Qual deve ser o momento de inércia na treliça da figura 45 em relação ao ponto A? Qual o
momento, em relação ao ponto E, causado pelo peso próprio da estrutura na mesma figura?
3.3.7Esquemabásicodemontagemdatreliça
Materiais: 14 barras de madeira ( 20 mm X 20 mm X 212,5 mm), anéis de PVCE (diâmetro de 75
mm e altura 20 mm), 14 parafusos,
Montagem:
i) Fure nas extremidades da madeira e parafuse os anéis formando a peça conforme a figura 41.
Figura 52.a. Montagem detalhada de
Figura 52.b. Montagem detalhada de
treliça com pseudo anel – parte 1.
treliça com pseudo anel – parte 2.
Fonte: Arquivo pessoal.
Fonte: Arquivo pessoal.
ii) Faça a conexão das extremidades através dos nós conectores. Esses conectores podem ser
feitos chapa metálica, cortada conforme indica a figura 53, para serem parafusados, rebitados ou
colados.
Figura 53. Aplicação de conectores em treliças.
Fonte: Arquivo pessoal.
3.3.8Atividade
1) Projete uma treliça plana de aço, secção cilíndrica de diâmetro 2 mm, contendo sete nós e
barras de densidade uniforme, onde deverá ser colocada entre dois pilares, a uma distância de 6
metros.
A densidade do aço é 7860 kg/m³. Desconsidere a massa de parafusos e dos conectores.
Calcule: a) a massa total da estrutura. b) as reações nos apoios se o centro de massa estiver no
centro geométrico. c) quais barras sofrem tração e compressão devido o peso da própria estrutura?
d) Quais os valores das trações e compressões?
(Problema) Se a treliça da figura 49 fosse de aço e recebesse mais 8 nós, nas mesmas proporções
geométricas e bi apoiada, a) qual deveria ser a quantidades de reações? b) As quantidades de
barras necessárias? Qual a metragem total de barras utilizadas? Seria possível estabelecer o
equilíbrio estático? Justifique as condições.
3.4 Visual Barras – Tutorial para Cálculo e Análise de Estruturas.
Para auxílio dos cálculos, depois de verificada a aprendizagem dos alunos, é sugerido neste
Roteiro a utilização do Visual Barras. É um software gratuito utilizado para cálculo de estruturas
metálicas. O programa é de uso técnico mas por apresentar uma interface amigável e exigir
poucas propriedades físicas nos computadores, pode ser utilizado para fins didáticos.
Desenvolvido por bolsistas de engenharia e arquitetura da Universidade de Passo fundo (UPF) no
programa de
apoio FAPERGS, encontra-se disponível no site: HTTP://www.etools.upf.br.
Depois de instalado, o programa apresenta a tela inicial,
Figura 54. Tela inicial do VB.
Fonte: Dados da pesquisa.
Ao clicar em “ler arquivos de dados” podem ser visualizadas estruturas pré projetadas. Para
executar um novo projeto deve-se trabalhar no modo interativo.
3.4.1 Iniciando um projeto
Clicando na opção treliça plana, poderá iniciar o processo de elaboração da treliça. (recomendase aqui para o aluno ter em mão o projeto da estrutura a ser montada).
3.4.2 Modos de interatividade
Na primeira tela escolha o modo interativo. O programa irá automaticamente mudar para o
segundo estágio de elaboração: Materiais e secções.
Na próxima etapa devem ser fornecidos dados referentes aos materiais utilizados na estrutura.
3.4.3 Número de materiais
Nesta opção devem ser escolhidas o número de materiais. Ex. se for colocado 2, poderá trabalhar
dois metais (ou materiais distintos). Para isso, deve-se clicar em confirmar para que possam ser
abertas as opções material 1 e o seu módulo de elasticidade, material 2 e seu módulo de
elasticidade. O material está na caixa de diálogo “ tipos de materiais”.
3.4.4 Materiais
Escolhido (s) o(s) material (is), escolha a seção do material, entre circular e retangular. Para
circular será solicitado o valor do diâmetro, para retangular, será solicitado o valor da altura e da
largura.
3.4.5 Coordenadas
Ao clicar em gravar informações, será aberta a nova aba, solicitando as coordenadas.
Figura 55. Configurando os nós no VB.
Fonte: Dados da pesquisa.
Nesta opção deve ser escolhida a quantidade de nós. Depois será solicitado para inserir as
coordenadas de cada nó. Clique em gravar as coordenadas. Será então aberta nova aba
“elementos”.
3.4.6 Barras
Nessa tela é gerado um pequeno gráfico (tela preta) onde são apresentadas as posições dos nós.
Clicando em confirmar, abrirá uma tabela onde serão inseridas as ligações de Cada elemento
(barras rígidas), ou seja, quando é escolhido um elemento, por exemplo, a barra 2, nó i = 2 e nó j
= 4, significa que a barra 2 liga as coordenadas do ponto 2 ao ponto 4. Confirme os dados e abrirá
a próxima aba “apoios”.
Figura 56. configurando apoios no VB.
Fonte: Dados da pesquisa.
Figura 57. Inserindo barras no VB.
Fonte: Dados da pesquisa.
3.4.7 Apoios
Os apoios são fixos e móveis, conforme discutido na seção 4.2.4.2.6 desse roteiro. Quando uma
estrutura apresenta dois apoios um deverá ser fixo e outro móvel, ou seja, um apoio permite
pequenos deslocamentos numa determinada direção. No VB, uma barra pode sofre deslocamento
e x e não permitir deslocamentos em y, para isso, o programa exige que dx=0 (permite
deslocamento na direção de x) e dx=1 ( não permite deslocamento em x).
Figura 58. Inserindo apoios no VB.
Fonte: Dados da pesquisa.
Note que o nó 1 permite deslocamento em x e não permite deslocamentos em y. O nó 5 não deve
permitir nenhum tipo de deslocamento. Obs.: Se os apoios forem determinados incorretamente, a
estrutura não permitirá nenhum tipo de análise. Ao escolher o modelo para os apoios, e clicando
em “gravar apoios” será aberta a aba de “cargas”.
Figura 59. Inserindo cargas no VB.
Fonte: Dados da pesquisa.
3.4.8 Cargas. Após gravar as cargas será aberta a aba para inserção da quantidade de cargas.
Coloque a quantidade de cargas desejadas e e aparecerá a opção de escolher o nó e as
componentes da forças na direção de x FX e na direção de y FY. Grave as cargas e abrirá a aba
de visualização da estrutura.
Figura 60. Visualização de estrutura no VB.
Fonte: Dados da pesquisa.
3.4.9 Análises dos resultados. Podem ser analisadas as variações elásticas ocorridas nas direções
axiais das barras, as reações nos apoios, os esforços de tração ou compressão.
Figura 61. Análise dos dados no VB.
Fonte: Dados da pesquisa.
3.4.10 Salvando o projeto da estrutura. Na aba da visualização é apresentado o ícone de um
disquete. Salve seu projeto colocando nome e a extensão vba. Exemplo: treliça01.vba.
3.4.11 Conclusão:
Existem diversos problemas em estática e problemas de física geral, como os problemas que
envolvem um corpo suspenso por dois cabos, que podem ser analisados pelo VB. A partir do
módulo de elasticidade e propriedades geométricas, podem ser idealizadas várias estruturas de
madeira, de aço, ferro, etc. Com uma interface relativamente amigável, diversos profissionais
podem ser treinados e posteriormente utilizar o software na elaboração e análise de estruturas.
Serralheiros poderão utilizar o programa na confecção de pequenas estruturas (currais, cancelas,
grades, etc), carpinteiros poderão utilizar para cálculos de pequenas peças de madeira
emestruturas simplificadas, ou outros profissionais na análise simplificada de pequenas estruturas.
O software representa uma ferramenta adicional que pode contribuir para qualificação dos
profissionais citados acima e se torna significativo no ensino por relacionar claramente elementos
utilizados no cotidiano com estruturas padronizadas. Os autores também advertem a utilização
desse software para cálculo de vários modelos estruturais, onde deverão ser acompanhados por
profissionais qualificados.
3.4.12 Atividade utilizando o Visual Barras
Procedimentos:
1. Utilizando o VB, insira os dados apresentados na estrutura abaixo, uma treliça de barras
circulares de diâmetro 2 mm e suporta duas cargas de 12kN e 8 kN conforme a figura.
2. Verifique os valores das trações e compressões e as reações de apoio. Coloque os dados na
tabela abaixo. Faça os cálculos e verifique os resultados teóricos com dos dados fornecidos pelo
programa.
Figura 62. Projeto de treliça.
Fonte: Dados da pesquisa.
Tabela 6. Análise de Forças em uma Estrutura Triangular.
AB
Barras
AC
BC
Tipo de Tensão
Tensões (kN) – dados do VB
Tenções (kN) – dados teóricos
3.4.13 Questionário
1) Quais facilidades e dificuldade de se utilizar o VB?
Reações nos apoios
R1X
RY1
R2X
R2Y
2) Quais fatores mais importantes devem ser considerados, em relação aos softwares no cálculo
de estruturas?
3) Como podem ser visualizadas as tensões no VB?
4) Qual deve ser o diâmetro mínimo para que cada barra venha suportar os esforços solicitados?
5) Utilizando a lei de Hooke, verifique os deslocamentos virtuais em cada barra.
3.4.14 Conclusões e discussões
3.4.15 Bibliografia
AMARAL, Otávio Campos. ESTRUTURAS ISOSTÁTICAS, 6. ed. Belo
Horizonte: Eng e Art, 1992
BEER, Ferdinand P., JOHNSTON JR., E. Russel. Resistência dos materiais. 3. ed.
São Paulo: Makron Books do Brasil, 1996.
CAMPANARI, FLAVIO A. TEORIA DAS ESTRUTURAS. Rio de Janeiro:
Guarnabara Dois, 1985.
MASUERO E CREUS. INTRODUÇÃO À MECÂNICA ESTRUTURAL.
Porto Alegre: Ed. Universidade, 1997.
MERIAN, J. C. ESTÁTICA. Rio de Janeiro: TC, 1995.
MOIOLA , C.H, MALITE, M. Análise teórica e experimental de treliças
metálicas espaciais construídas com extremidades estampadas. São Carlos:
EESC-USP, 2002.
NOGUEIRA, J.B. Mecânica dos solos – Ensaios de laboratório, São Carlos:
EESC-USP, 1995.
UNIVERSIDADE DE BRASILIA. FACULADADE DE ARQUITETURA E
URBANISMO. 2005. Tipologias Arquitetônicas de Estruturas Espaciais em
Brasília. Disponível em: http://www.docomomo.org.br/seminario%205%20pdfs/
036R. pdf, acesso em 06 de maio de 2010.
UNIVERSIDADE ESTADUAL DE LONDRINA. DEPARTAMENTO DE
MATEMÁTICA. 2007. Disponível em: http://www.mat.uel.br/geometrica/php/tru/
tru_3t/tru_3_a.php , acesso em 1 de abril de 2010.
INSTITUTO SUPERIOR DE ENGENHARIA DE LISBOA. DEPARTAMENTO DE
ENGENHARIA. 2005. Disponível em: http://www.dec.isel.ipl.pt/anexos_ disciplinas
/Mecânica_Aplicada/ Aula_laboratorial /Trelica.pdf, acesso em 02 de abril de 2010.
INSTITUTO SUPERIOR DE ENGENHARIA DE LISBOA. DEPARTAMENTO DE
ENGENHARIA. 2005. Disponível em:http://www.dec.isel.ipl.pt/anexos_disciplinas/
Mecânica_Aplicada/CapIV.pdf, acesso em 06 de abril de 2010.
UNIVERSIDADE FEDERAL DE UBERLÂNDIA. NOTAS DE AULAS DE
ENGENHARIA CIVIL. 2003. Disponível em: http://usuarios.upf.br/~zacarias /Notas_
de_Aula_Madeiras.pdf, acesso em 30 de abril de 2010.
CENTRO BRASILEIRO DE CONSTRUÇÕES EM AÇO. FERRAMENTAS
COMPUTACIONAIS PARA O ENSINO DE ESTRUTURAS. 2008. Disponível
em: http://www.etools.upf.br, acesso em 4 de maio de 2010.
USP. DEPARTAMENTO DE ESTRUTURAS. 2008. Tipos de Análise Estrutural para
Elementos Lineares Segundo a NBR 6118:2003. Disponível em: http://www.set.eesc
.usp.br, acesso em 16 de Abril de 2010.
FEIRA DE CIÊNCIAS. Sala 6, ESTÁTICA. Disponível em : http://
www.feiradeciencias. com.br/sala05/05_ RE_08.asp , acesso em 30 de abril de 2010