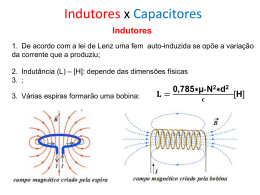
Eletromagnetismo – Aula 8
Maria Augusta Constante Puget (Magu)
Indutor (1)
Um indutor é um dispositivo elétrico
passivo que armazena energia na forma
de campo magnético.
 O indutor pode ser utilizado em circuitos
como um filtro passa baixa, rejeitando as
altas frequências.
 Dois (ou mais) indutores acoplados formam
um transformador, que é um componente
fundamental de qualquer rede elétrica
nacional.

2
Indutor (2)
Um indutor é geralmente construído como
uma bobina (solenóide) de material
condutor.
 Por esta razão, o símbolo utilizado para
representar um indutor é:

3
Indutor (3)
Um fio conduzindo corrente gera um
campo magnético ao seu redor.
 Para obtermos a direção e o sentido do
campo magnético devido a uma corrente i
em um fio condutor longo e retilíneo
usamos a regra da mão direita.

4
Indutor (4)
Um solenóide é um fio condutor enrolado
em uma hélice com as voltas bem próximas
entre si.
 O papel do solenóide no magnetismo é
análogo ao do capacitor de placas
paralelas, que produz um campo elétrico
intenso e uniforme entre suas placas.

5
Indutor (5)

Um solenóide é usado para produzir um
campo magnético uniforme e intenso na
região da vizinhança de seus anéis.
6
Indutância (1)
Indutância é a grandeza física associada aos
indutores.
 É simbolizada pela letra L.
 A indutância, assim como a capacitância, depende
apenas das propriedades geométricas do
indutor e do material de que é constituído.
 Para um solenóide, temos:
𝐿 = 𝜇0 𝑛2 𝑙𝐴
onde:
0 = Constante de permeabilidade do material.
l = Comprimento do solenóide.
A = Área de seção transversal do solenóide.
n = Número de espiras por unidade de comprimento
do solenóide.

7
Indutância (1)
A unidade de indutância no
SI é o henry (H), em
homenagem
ao
físico
americano Joseph Henry,
descobridor da lei da
indução e contemporâneo
de Faraday.
 Trata-se de uma unidade
derivada:
1 henry = 1 H = 1Tm2/A

8
Combinação de Indutores (1)

A análise de um circuito pode ser, muitas vezes,
simplificada substituindo-se uma combinação de
dois ou mais indutores por um único indutor
equivalente que tenha a mesma corrente e a
mesma queda de potencial que a combinação de
indutores.

Duas combinações básicas entre indutores são:
◦ Associação em paralelo.
◦ Associação em série.
9
Indutores em Série (1)
Para indutores em série, a indutância equivalente é dada por:
𝑛
𝐿𝑆 =
𝐿𝑗
𝑗=1
10
Indutores em Paralelo (1)
Para indutores em paralelo, a indutância equivalente é dada por:
1
=
𝐿𝑃
𝑛
𝑗=1
1
𝐿𝑗
11
Energia Armazenada em um
Campo Magnético (1)
A energia (medida em joules, no SI) armazenada
num indutor é igual à quantidade de trabalho
necessária para estabelecer o fluxo de corrente
através do indutor e, consequentemente, o
campo magnético.
 É dada por:

𝐿𝑖 2
𝑈𝐵 =
2
12
Circuito RL (1)
Vamos supor um indutor de indutância L,
conectado em série a um resistor de resistência
R e a uma bateria ideal de fem E, conforme
mostra a figura.
 Aplicando a lei das malhas a este circuito,
percorrendo-o no sentido horário, partindo do
terminal negativo da bateria, chegamos à
i
seguinte equação:

E −𝑖R
𝑑𝑖
−L
𝑑𝑡
=0
E
13
Circuito RL (2)
Esta equação pode ser reescrita como:
𝑑𝑖
𝑖R + L = E
𝑑𝑡
que tem uma estrutura semelhante à equação para
o circuito RC.
 Assim, a solução desta equação que satisfaz a
condição de que em t = 0, i(0) = 0 é:
i
E
i 𝑡 =
(1 − 𝑒 −𝑅𝑡/𝐿 )

𝑅
E
14
Circuito RL (3)
Observar na solução:
E
i 𝑡 =
(1 − 𝑒 −𝑅𝑡/𝐿 )

𝑅
que:
◦ Para t = 0, i0 = 0.
◦ Quando t , o termo exponencial vai a zero e i =
E/R.
i
E/R
15
Circuito RL (4)
Depois de atingido o valor estacionário da
corrente, vamos supor que a bateria seja retirada
do circuito.
 Aplicando a lei das malhas a este novo circuito,
temos:

𝑑𝑖
𝑖R + L = 0
𝑑𝑡
Esta equação é semelhante à equação de
descarga do capacitor. Sua solução é:
𝑖 𝑡 = 𝑖0 𝑒 −𝑅𝑡/𝐿
onde i0 é a corrente inicial que atravessa o indutor.

16
Circuito RL (5)


𝑖 𝑡 = 𝑖0 𝑒 −𝑅𝑡/𝐿
Esta expressão nos diz que a corrente i diminui
exponencialmente com o tempo a uma taxa que é
determinada pela constante de tempo indutiva  = L/R.
Observe que um maior valor de  corresponde a um
maior tempo de descarga.
i
i0
17