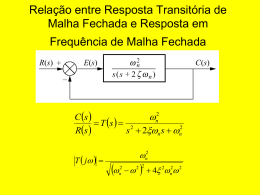
Controle Linear II
Resposta no Tempo de Sistemas
em Malha Fechada
Resposta no Tempo de Sistemas em Malha
Fechada

Seja o sistema de controle digital em malha fechada
apresentado na figura abaixo. Determine a resposta no
tempo deste sistema a uma entrada degrau.
Resposta no Tempo de Sistemas em Malha
Fechada

Como visto anteriormente, a função de transferência em
malha fechada do sistema é:
C ( z)
G( z)

R( z ) 1  G ( z )

Sendo G(z) determinado por:
Resposta no Tempo de Sistemas em Malha
Fechada

Então, a função de transferência do sistema será:
0,368z  0,264
G( z)
z 2  1,368z  0,368

T ( z) 
1  G ( z ) 1  0,368z  0,264
z 2  1,368z  0,368
0,368z  0,264
0,368z  0,264
z 2  1,368z  0,368
z 2  1,368z  0,368

T ( z)  2
z 2  z  0,632
z  1,368z  0,368 0,368z  0,264
z 2  1,368z  0,368
z 2  1,368z  0,368
Resposta no Tempo de Sistemas em Malha
Fechada

Então, a função de transferência do sistema será:

0,368z  0,264
z 2  1,368z  0,368
T ( z)  2

z  1,368z  0,368 z 2  z  0,632
T ( z) 

0,368z  0,264
z 2  z  0,632
Sendo a função degrau, na transformada Z, dada abaixo, a
saída do sistema será:
z
R( z ) 
z 1
C ( z)  T ( z) 
z
z 1
Resposta no Tempo de Sistemas em Malha
Fechada

Saída do sistema:
0,368z  0,264 z
0,368z 2  0,264z
C ( z)  2

 3
z  z  0,632 z  1 ( z  2 z 2  1,632z  0,632)
C ( z )  0,368z 1  z  2  1,4 z 3  1,4 z  4  1,15z 5  0,9 z 6 
 0,8 z 7  0,87z 8  0,99z 9  1,08z 10  1,08z 11  z 12  0,98z 13  ...

O valor final de c(kT), quando k ∞:
lim
z 1
0,632
( z  1)C ( z ) 
1
0,632
Resposta no Tempo de Sistemas em Malha
Fechada

Simulação do sistema:
Resposta no Tempo de Sistemas em Malha
Fechada

Simulação do sistema:
Mapeamento entre Plano-S e
Plano-Z
Mapeamento entre Plano-S e Plano-Z
Mapeamento entre Plano-S e Plano-Z
Mapeamento entre Plano-S e Plano-Z

Matematicamente, também podemos relacionar os pólos
entre o plano-S e o plano-Z:

Seja a função de transferência
de segunda ordem no plano-S:
Os pólos serão:

Esses pólos no plano-S serão
equivalentes aos pólos do
plano-Z:
Mapeamento entre Plano-S e Plano-Z

Com a relação dada no slide anterior, e fazendo algumas
manipulações matemáticas, obtemos os parâmetros de
coeficiente de amortecimento, frequência natural e constante
de tempo para o sistema de segunda ordem:

Coeficiente de amortecimento:
Frequência natural:
Constante de tempo:
n 

1
ln 2 r   2
T
1
n

T
ln r
 ln r
ln 2 r   2
Equação Característica
Equação Característica

Considere o sistema de malha fechada apresentado na figura
abaixo:

A função de transferência do sistema é:
T ( z) 

G( z)
1  GH ( z )
A equação característica (EC) do sistema é:
1  GH ( z)  0
As raízes da EC são os pólos da
função de transferência em
malha fechada.
Exemplo

Seja o sistema apresentado abaixo:

A função de transferência do sistema será:
G( z )
0,368z  0,264
 2
1  G ( z ) z  z  0,632

A equação característica do sistema é:
1  G( z )  0
z 2  z  0,632  ( z  0,5  j 0,618)(z  0,5  j 0,618)  0
Exemplo

Os pólos do sistema são complexos e localizados em:
z  0,5  j 0,618  0,795  51  0,795  0,89 rad

Com esses dados podemos obter o coeficiente de
amortaecimento, a frequência natural e a constante de tempo
do sistema:
Lembrando que z  r    r  T
Logo,
Exemplo

Se compararmos os valores do coeficiente de
amortecimento, frequência natural e constante de tempo
do sistema, veremos que os valores quando o
controle é totalmente analógico difere dos valores
quando o controle é digital. Isto se deve ao fato do
período de amostragem ser alto.
  0,25
n  0,9191 rad / s
  4,36s
  0,5
n  1 rad / s
  2s
Exemplo

Para que a amostragem não tenha efeito sobre o sistema,
o período de amostragem T deve ser muito
menor do que a constante de tempo τ do sistema.
T


 1
ou

1

T
ln r
A razão τ/T é simplesmente o número de amostras por
constante de tempo.
Estabilidade de Sistemas
Discretos
Estabilidade de Sistemas Discretos

Nesta seção será estudada a estabilidade de sistemas de
controle discretos no tempo.

Considere o seguinte sistema:
C( z)
G( z )

R( z ) 1  GH ( z )

A estabilidade do sistema acima será determinada pela
localização dos pólos em malha fechada no plano-Z:
P( z)  1  GH ( z)
Estabilidade de Sistemas Discretos

Assim, tomando a EC do sistema analisamos:
P( z)  1  GH ( z)



Para o sistema ser estável, os pólos em malha fechada ou as
raízes da EC devem estar dentro do círculo unitário no
plano-Z. Qualquer pólo em malha fechada que estiver fora do
círculo torna o sistema instável.
Se um único pólo estiver em z=1 (ou pólos complexos em
|z|=1), o sistema se torna criticamente estável. Mais de um
pólo em cima do círculo unitário torna o sistema instável.
Os zeros em malha fechada não afetam a estabilidade absoluta
do sistema e portanto, podem estar localizados em qualquer
lugar do Plano-Z.
Estabilidade de Sistemas Discretos

Exemplo

Considere o sistema de controle da figura abaixo. Determine a
estabilidade do sistema quando K =1.

Solução
1  e Ts
1
G( s) 
s s( s  1)
1  e Ts
1  0,3679z  0,2642
G( z )  Z 

 s s( s  1)  ( z  0,3679)(z  1)
Estabilidade de Sistemas Discretos

Exemplo

Sendo a função de transferência em malha fechada,
C ( z)
G( z)

R( z ) 1  G ( z )

A equação característica é:
1  G( z)  0
1
0,3679z  0,2642
0
( z  0,3679)(z  1)
( z  0,3679)(z  1)  0,3679z  0,2642
0
( z  0,3679)(z  1)
Estabilidade de Sistemas Discretos

Exemplo

Equação Característica:
( z  0,3679)(z  1)  0,3679z  0,2642
0
( z  0,3679)(z  1)
( z  0,3679)(z  1)  0,3679z  0,2642 0

z 2  z  0,6321 0

z1  z2  1
As raízes da EC são:
z  0,5  j 0,6181
Como,

Logo, o sistema é
estável.
Estabilidade de Sistemas Discretos – Testes
de Estabilidade

Três testes de estabilidade podem ser aplicados
diretamente a equação característica, P(z) = 0, sem ter
que resolver as raízes dessa equação.

Esses testes são:

Teste de estabilidade Schur-Cohn

Teste de estabilidade Jury

Transformação bilinear (Critério de Routh-Hurwitz)
Estabilidade de Sistemas Discretos – Testes
de Estabilidade

Os dois primeiros testes revelam a existência de
possíveis raízes instáveis ( raízes que se localizam fora do
círculo unitário no plano Z);

Ambos os testes ( Schur-Cohn e Jury) podem ser
aplicados a equações polinomiais com raízes reais ou
complexas.

Entre os testes, daremos ênfase ao teste de estabilidade
de Jury.
Estabilidade de Sistemas Discretos – Teste
de Estabilidade de Jury

Um critério de estabilidade para sistemas discretos muito
utilizado é o critério de Jury (ou teste de estabilidade de
Jury).

O teste de Jury é aplicado a partir de uma equação
característica P(z).

Uma tabela será construída sendo os elementos da tabela
dados pelos coeficientes da equação característica P(z).
Estabilidade de Sistemas Discretos – Teste
de Estabilidade de Jury

Seja a equação característica de um sistema discreto
expressa como:
P( z)  an z n  an1z n1  ... a1z  a0  0

A tabela para o
teste de Jury é
então
formada
como apresentada
ao lado:
Estabilidade de Sistemas Discretos – Teste
de Estabilidade de Jury

As linhas “pares” da tabela são os elementos da linha
anterior, mas com a ordem invertida.

Já os elementos das linhas “ímpares” são formados a
partir dos determinantes:
Estabilidade de Sistemas Discretos – Teste
de Estabilidade de Jury
As condições necessárias e suficientes para que a EC P(z)
não tenha raízes fora do círculo unitário são:

(1) P( z ) z 1  0

(2) (1) n P( z ) z  1  0

(3) a0  an
b0  bn 1

c0  cn  2
d 0  d n 3

m0  m2
O teste de Jury pode ser aplicado da
seguinte maneira:

Teste as três primeiras condições (1), (2)
e (3). Pare se uma dessas não for
satisfeita.
Construa a tabela e teste as condições
seguintes. Pare se uma das condições
não for satisfeita.
Para sistemas de ordem n, serão
necessárias um total de n+1
restrições.
Estabilidade de Sistemas Discretos – Teste
de Estabilidade de Jury

Exemplo 2

Suponha que a eq. característica de um sistema discreto em
malha fechada é dada pela expressão:
P( z)  z 3 1,8z 2  1,05z  0,2  0

Solução
A ordem do sistema é 3 (n = 3).
Para essa EC temos:
P( z )  an z n  an 1 z n 1  ...  a1 z  a0  0
P( z )  a3 z 3  a2 z 2  a1 z1  a0  0
a3  1
a2  1,8
a1  1,05
a0  0,2
Estabilidade de Sistemas Discretos – Teste
de Estabilidade de Jury

Exemplo 2

Primeiramente, iremos analisar as três primeiras condições:
(1) P( z ) z 1  0
P(1)  (1)3  1,8(1) 2  1,05(1)  0,2
ok
P(1)  0,05  0
(2) (1) n P( z ) z  1  0
(1) 3 P(1)  [(1) 3  1,8(1) 2  1,05(1)  0,2]
(1) 3 P(1)  4,05  0
(3) a0  an
a0  a3
 0,2  1
ok
ok
Estabilidade de Sistemas Discretos – Teste
de Estabilidade de Jury

Exemplo 2

Passaremos para a construção da tabela de Jury:
Como a ordem do sistema é 3, iremos
analisar até a 4a restrição.
Estabilidade de Sistemas Discretos – Teste
de Estabilidade de Jury

Exemplo 2

Passaremos para a construção da tabela de Jury:
b0  bn1  b0  b2  0,96  0,69
ok
Estabilidade de Sistemas Discretos – Teste
de Estabilidade de Jury

Portanto, como todas as restrições possíveis foram
satisfeitas, concluímos que o sistema é estável.
P ( z ) z 1  0
( 1) n P ( z ) z  1  0
a0  a n
ok
b0  bn 1

Podemos ver essa mesma situação (sistema estável) ao
fatorarmos a EC:
P( z)  ( z  0,5)2 ( z  0,8)