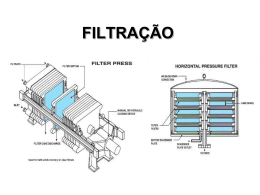
ESCOLA DE ENGENHARIA DE LORENA - USP
DEPARTAMENTO DE ENGENHARIA QUÍMICA
FILTRAÇÃO
PROF. DR. FÉLIX MONTEIRO PEREIRA
FILTRAÇÃO SÓLIDO-LÍQUIDO
Alimentação
Meio
Torta
Filtrado
poroso
Na filtração, as partículas
sólidas suspensas em um
fluido são separadas usando
um meio poroso.
Ele separa as partículas em
uma fase sólida (“torta”) e
permite o escoamento de um
fluido claro (“filtrado”).
O fluido pode ser um gás ou um líquido.
O produto pode ser tanto o fluido clarificado
quanto a torta de partículas sólidas.
Aplicações em função das características da
suspensão:
O princípio da filtração industrial e o do
equipamento de laboratório é o mesmo,
apenas muda a quantidade de material a
ser filtrado.
Bomba
de vácuo
Filtro de
Papel
O aparelho de filtração de
laboratório mais comum é
denominado filtro de Büchner.
O líquido é colocado por cima e flui
por ação da gravidade e no seu
percurso encontra um tecido
poroso (um filtro de papel).
Como a resistência à passagem
pelo meio poroso aumenta no
decorrer do tempo, usa-se um
vaso Kitasato conectado a uma
bomba de vácuo.
Os filtros industriais podem ser feitos para funcionar:
em batelada (a torta é retirada depois de cada corrida) ou
de forma contínua (a torta sólida é retirada continuamente).
Os filtros podem funcionar:
- por ação da gravidade, o líquido flui devido a existência
de uma coluna hidrostática;
- por ação de força centrífuga;
- por meio da aplicação de pressão ou vácuo para
aumentar a taxa de fluxo.
O meio de filtração pode ser:
- um leito poroso de materiais sólidos inertes,
- um conjunto de placas, marcos e telas em uma prensa,
- um conjunto de folhas duplas dentro de um tanque,
- um cilindro rotativo mergulhado na suspensão,
- ou discos rotativos mergulhados na suspensão.
- ou bolsas ou cartuchos dentro de uma carcaça.
Filtros de leito fixo
Entrada do líquido
Partículas sólidas separadas
Defletor
Placa metálica
perfurada ou com
ranhuras
Partículas finas
Partículas grossas
Líquido clarificado
O tipo de filtro mais simples.
Se usa no tratamento de água potável, quando se tem grandes
volumes de líquido e pequenas quantidades de sólidos.
A camada de fundo é composta de cascalho grosso que
descansa em uma placa perfurada ou com ranhuras. Acima do
cascalho é colocada areia fina que atua realmente como filtro.
Filtro prensa
Um dos tipos mais usados na industria.
Usam placas e marcos colocados em forma alternada.
Utiliza-se tela (tecido de algodão ou de materiais sintéticos)
para cobrir ambos lados das placas.
Filtro de tecido
Alimentação
Filtrado
Marco
Torta
Placa
Filtro-Prensa
A alimentação é bombeada à prensa e flui pelas armações.
Os sólidos acumulam-se como “torta” dentro da armação.
O filtrado flui entre o filtro de tecido e a placa pelos canais
de passagem e sai pela parte inferior de cada placa.
Filtro de tecido
A filtração prossegue até o
espaço interno da armação
esteja completamente
preenchida com sólidos.
Alimentação
Filtrado
Marco
Torta
Placa
Nesse momento a armação
e as placas são separadas e
a torta retirada. Depois o
filtro é remontado e o ciclo
se repete.
Filtros de “folhas”
Foi projetado para grandes volumes de líquido e para ter uma
lavagem eficiente.
Cada folha é uma armação de metal oca coberta por um filtro
de tecido. Elas são suspensas em um tanque fechado.
A alimentação é introduzida no tanque e
passa pelo tecido a baixa pressão.
A torta se deposita no exterior da folha.
O filtrado flui para dentro da armação oca.
Após a filtragem, ocorre a limpeza da
torta. O líquido de lavagem entra e segue
o mesmo caminho que a alimentação.
A torta é retirada por uma abertura do
casco.
Filtros de folhas
Filtro de tambor a vácuo, rotativo e contínuo.
Ele filtra, lava e descarrega a
torta de forma contínua.
O tambor é recoberto com um
meio de filtração conveniente.
Uma válvula automática no
centro do tambor ativa o ciclo
de filtração, secagem, lavagem
e retirada da torta.
O filtrado sai pelo eixo de rotação.
Existem passagens separadas
para o filtrado e para o líquido de
lavagem.
Há uma conexão com ar
comprimido que se utiliza para
ajudar a raspadeira de facas na
retirada da torta.
Ciclo de lavagem
Secagem
Secagem
Descarga
Carga
Suspensão
Válvula automática
Formação da torta
Filtro de tambor a vácuo, rotativo e contínuo.
Filtro de tambor a vácuo, rotativo e contínuo.
Filtro contínuo de discos rotativos
É um conjunto de discos verticais que giram em um eixo de
rotação horizontal. Este filtro combina aspectos do filtro de
tambor rotativo a vácuo e do filtro de folhas.
Cada disco (folha) é oco e coberto com um tecido e é em
parte submerso na alimentação. A torta é lavada, secada, e
raspada quando o disco gira.
Filtro de Cartucho
O filtro de cartucho é de operação
contínua e limpeza automática. É
composto de uma carcaça onde se
colocam cartuchos (ou bolsas).
O gás “sujo” é forçado a passar
através dos cartuchos, em cuja
superfície as partículas são retidas.
O gás limpo é conduzido à parte
interna do filtro e em seguida ao
exaustor.
O processo de limpeza do cartucho
é feito automaticamente através de
pulsos de ar comprimido.
Meios de Filtração e Auxiliares de Filtração
1. Meios de filtração.
O meio para filtração industrial deve:
• Retirar o sólido a ser filtrado da alimentação e gerar
um filtrado claro.
• Permitir que a torta com filtro seja removida de forma
fácil e limpa.
• Ser forte o suficiente para não rasgar e ser
quimicamente resistente às soluções usadas.
• Para que a taxa da filtração não fique muito lenta os
poros devem ficar livres e não ser obstruídos.
Auxiliares de Filtração
Certos compostos podem ser usados para ajudar a
filtração, como a terra de diatomáceas que é formada
principalmente de sílica. Também são empregados a
celulose de madeira e outros sólidos porosos inertes.
Esses compostos podem ser usados de vários modos:
1. Como pré-cobertura antes da filtração.
O auxiliar de filtração prevenirá os sólidos gelatinosos de entupir
o filtro e também permitirá um filtrado mais claro.
2. Acrescentados à alimentação antes da filtração.
Aumenta a porosidade da torta e reduz a resistência da torta
durante a filtração.
3. Em um filtro rotativo, o auxiliar de filtração pode ser
aplicado como uma pré-cobertura. Posteriormente, as fatias
finas desta camada são cortadas junto com a torta.
Teoria Básica de Filtração
Queda de pressão de fluido através da torta
A figura mostra uma seção de um filtro em um tempo t (s)
medido a partir do início do fluxo. A espessura da torta é L
(m). A área da seção transversal é A (m2), e a velocidade
linear do filtrado na direção L é v (m/s)
Meio filtrante
Alimentação
da suspensão
Filtrado
Incremento da torta
A equação de Poiseuille explica o fluxo laminar em
um tubo, que no sistema internacional de unidades (SI)
pode ser descrito como:
P 32 v
 2
L
D
Onde:
∆p é a pressão (N/m2)
v é a velocidade no tubo (m/s)
D é o diâmetro (m)
L é o comprimento (m)
µ é a viscosidade (Pa.s)
No caso de fluxo laminar em um leito empacotado de
partículas a equação de Carman-Kozeny tem sido aplicada
à filtração com sucesso:
P 32 v
 2
L
D
Onde:
pc
k1  v (1   ) S

3
L

2
k1 é uma constante para partículas de tamanho e forma definida
µ é a viscosidade do filtrado em Pa.s
v é a velocidade linear em m/s
ε é a porosidade da torta
L é a espessura da torta em m
S0 é a área superficial específica expressa em m2 / m3
∆Pc é a diferença de pressão na torta N/m2
2
0
A velocidade linear é baseada na área da seção transversal
vazia:
dV / dt
v
A
Onde:
A é a área transversal do filtro (m2)
V é o volume coletado do filtrado em m3 até o tempo t (s).
A espessura da torta L depende do volume do filtrado V
são obtidas a partir do balanço material.
mp  cs Vtotal
LA (1   )  p  cs (V  LA)
Onde:
cs = kg de sólidos/m3 do filtrado,
ρp é a densidade de partículas sólidas na torta em kg/m3
cs (V  LA)
L
A (1   )  p
dV / dt
v
A
pc
k1  v (1   ) S

L
3
pc
dV

k1 (1   ) S 02 csV
A dt
 p 3
A
2
2
0
pc
dV

A dt  csV
A
Para a resistência do leito temos:
Onde α é a resistência específica da
torta (m/kg) definida como:
pc
dV

A dt  csV
A

k1 (1   )S02
 p 3
Para a resistência da tela filtrante, podemos usar a
Equação de Darcy:
dV p f

A dt Rm
Onde:
Rm é a resistência ao fluxo do meio filtrante (m-1)
∆Pf é a queda de pressão no filtro
pc
dV

A dt  csV
A
dV p f

A dt Rm
Como as resistências da torta e do meio filtrante estão
em série, podem ser somadas:
dV
p

A dt
 csV


 Rm 
 A

Onde ∆p = ∆pc (torta) + ∆pf (filtro)
dV
p

A dt
 c V

  s  Rm 
 A

A equação anterior pode ser
invertida para dar:
cs
dt

 2
V
Rm
dV A (p)
A(p)
Onde Kp está em s/m6 e B em s/m3:
Kp 
cs
A (p)
2
B
Rm
A (p)
dt
 K pV  B
dV
Filtração à pressão constante
Para pressão constante e α constante (torta incompressível),
V e t são as únicas variáveis.
cs
dt

 2
V
Rm
dV A (p)
A(p)
dt
 K pV  B
dV
Integração para obter o tempo da filtração t em (s):

t
0
v
dt   ( K pV  B) dV
0
t
Kp
2
V  BV
2
Dividindo por V:
t Kp

V B
V 2
Onde V é o volume total do filtrado (m3) reunido em t (s)
Para saber o tempo de filtração é necessário conhecer
α e Rm.
Kp 
t
Kp
2
V  BV
2
B
cs
A2 (p)
Rm
A (p)
Para isso, posso utilizar a equação dividida por V:
t Kp

V B
V 2
E traçar um gráfico de t/V versus V
Preciso dos dados de volume coletado (V) em tempos
diferentes de filtração.
t Kp
 V B
V 2
1 cs

2 2 A2 (p)
Kp
Y = A.X + B
t/V
B
V
Rm
A (p)
Kp = coeficiente angular da reta
t Kp
 V B
V 2
B = coeficiente linear da reta
1 cs

2 2 A2 (p)
Kp
Com Kp e B pode-se determinar
diretamente o tempo de filtração.
B
Rm
A (p)
t
Kp
2
V 2  BV
Porém o cálculo de  (resistência específica da torta) e de
Rm (resistência do meio filtrante) permite obter a equação do
tempo de filtração em termos dos parâmetros básicos da
operação
cs
Rm
2
t 2
V 
V
2 A (p)
A (p)
Exercício:
Avaliação das Constantes para Filtração à Pressão
Constante
Contam-se com os dados da filtração em laboratório de
uma suspensão de CaCO3 em água a 298,2 K (25°C) e a
uma pressão constante (∆p) de 338 kN /m2.
Área do filtro prensa de placa-e-marco
A = 0,0439 m2
Concentração de alimentação
cs = 23,47 kg/m3
Calcule as constantes α e Rm a partir dos dados
experimentais de volume de filtrado (m3) versus tempo de
filtração (s). Estime o tempo necessário para filtrar 1m3
da mesma suspensão em um filtro industrial com 1m2 de
área. Se o tempo limite para essa filtração fosse de 1h,
qual deveria ser a área do filtro?
Tempo (s)
B
10-3
4,4
0,498 x
9,5
1,000 x 10-3
16,3
1,501 x 10-3
24,6
2,000 x 10-3
34,7
2,498 x 10-3
46,1
3,002 x 10-3
59,0
3,506 x 10-3
73,6
4,004 x 10-3
89,4
4,502 x 10-3
107,3
5,009 x 10-3
Rm
A (p)
Kp 
Volume (m3)
cs
A2 (p)
A = 0,0439 m2
cs = 23,47 kg/m3
µ = 8,937 x 10-4 Pa.s
(água a 298,2 K)
(∆p) = 338 kN/m2
cs
A2 (p) 2 Rm
t
V 
V
2
A (p)
Solução:
Dados são usados para obter t/V
t
V x 103
(t/V) x 10-3
t/V
25000
4,4
0,498
8,84
9,5
1,000
9,50
20000
16,3
1,501
10,86
15000
24,6
2,000
12,30
34,7
2,498
13,89
46,1
3,002
15,36
5000
59,0
3,506
16,83
0
73,6
4,004
18,38
89,4
4,502
19,86
107,3
5,009
21,42
10000
y = 3E+06x + 6786
R² = 0.9965
0
0.001
0.002
0.003
0.004
0.005
V
0.006
ΔY
 3000000
ΔX
Solução:
Dados são usados para obter t/V
Y  3 x 10 6 X  B
25000
20000
B = 6400 s/m3
15000
10000
y = 3E+06x + 6786
R² = 0.9965
5000
Kp/2 = 3,00 x 106 s/m6
Kp = 6,00 x 106 s/m6
0
0
0.001
0.002
0.003
0.004
0.005
0.006
  cs
(8,937 x104 ) ( ) (23,47)
K p  6,00 x10  2

A (p)
(0,0439) 2 (338 x 103 )
6
 1,863x1011 m / kg
μRm
(8,937x 104 )(Rm )
B  6400

A(  Δp) 0,0439(338x 103 )
Rm  10,63x 1010 m 1
Solução:
cs
Rm
2
t 2
V 
V
2 A (p)
A (p)
(8,937 x 10-4 )(1,863 x 1011 )(23,47) 2 (8,937 x 104 )(10,63 x 1010 )
t
1 
1
2
3
3
2 x1 x(338 x 10 )
1(338 x 10 )
t  6061,78 segundos  1,68 horas
Solução:
cs
Rm
2
t 2
V 
V
2 A (p)
A (p)
5710 286
t 2 
A
A
t  3600 s
3600A2  286A  5710 0
A  1,3m 2
Compressibilidade da torta
Torta incompressível (α = constante): um aumento na vazão
acarreta em um aumento proporcional da queda de pressão
(∆p), ou seja, para dobrar a vazão da filtração, deve-se
dobrar (∆p).
dV
p

A dt
 csV


 Rm 
 A

Torta compressível (α = f(∆p)): um aumento na vazão
acarreta em um aumento maior que o proporcional da queda
de pressão (∆p), ou seja, para dobrar a vazão da filtração,
deve-se utilizar uma (∆p) maior que o dobro.
Equação empírica comumente utilizada:
s é o fator de compressibilidade
  0 ps
varia entre 0,2 e 0,8, na prática.
s = 0 para torta incompressível
Exercício:
Filtrações a pressão constante foram realizadas para uma suspensão de
CaCO3 em H2O sendo obtidos os resultados apresentados na tabela. A
superfície total de filtração foi 440 cm², a massa de sólidos por volume de
filtrado foi de 23,5 g/L e a temperatura foi de 25 oC (H2O=0,886x10-3kg/[m
s]). Calcule os valores de  e Rm em função da diferença de pressão e
elabore uma correlação empírica entre  e P.
Experimento:
P
V(L)
0,5
1
1,5
2
2,5
3
3,5
4
4,5
5
5,5
6
1
5x104
t1
13,7
46,7
99,1
170,8
261,8
372,2
2
1x105
t2
8,2
28,2
60,2
104,1
159,9
227,5
307,1
398,6
3
2x105
t3
4,9
17,2
36,7
63,7
97,9
139,4
188,3
244,5
308,1
378,9
4
4 x105
t3
2,9
10,4
22,3
38,8
59,8
85,3
115,3
149,8
188,8
232,3
280,4
332,9
5
8 x105
t5
1,7
6,3
13,6
23,6
36,5
52,1
70,5
91,7
115,6
142,4
171,9
204,1
Solução:
V
0,0005
0,001
0,0015
0,002
0,0025
0,003
0,0035
0,004
0,0045
0,005
0,0055
0,006
t1/V
27391
46728
66065
85402
104739
124076
t2/V
16333
28236
40140
52043
63946
75849
87753
99656
t3/V
9844
17172
24499
31826
39153
46481
53808
61135
68463
75790
t4/V
5870
10380
14891
19401
23912
28422
32933
37443
41953
46464
50974
55485
t5/V
3481
6258
9034
11811
14587
17364
20140
22917
25693
28470
31247
34023
Regressão linear:
t/V=aV+B  a= Kp/2=c/(2A2p), B=Rm/(Ap)
= 0 ps  log()=log(0) + s log(p)
Solução:
Regressão linear:
t/V=aV+B  a=c/(2A2p), B=Rm/(Ap)
= 0 ps  log()=log(0) + s log(p)
P
a (s/m^6)
B(s/m^3)
(m/kg)
Rm(1/m)
5 x104
3,8674x107
8054,5
3,6x1011
2,0x1010 4,69897 11,55582
1 x105
2,3806x107
4430,0
4,43x1011 2,2x1010 5,00000 11,64613
2 x105
1,4655x107
2517,0
5,45x1011 2,5x1010 5,30103 11,73644
4 x105
9,0210x106
1359,2
6,71x1011 2,7x1010 5,60206 11,82675
8 x105
5,5530x106
704,8
8,26x1011 2,8x1010 5,90309 11,91706
log(0)=10,146  0 = 1,4x1010 m/kg
s=0,3
  1,4 1010 P 0,3
log(p)
log()
Exercício:
Um filtro prensa com a área de abertura do quadro igual a 1 m2 e espessura do quadro de 1 cm
utiliza 20 quadros para filtrar a suspensão de CaCO3 utilizada no ensaio anterior. Admitindo que a
pressão compressiva utilizada seja de 300 kPa, que a massa específica da torta (seca) formada
seja de torta=1600 kg/m3 e a do CaCO3 seja sólido=2800 kg/m3.
a) Calcule a área total de filtração;
b) Calcule o volume total dos quadros;
c) Calcule a porosidade  da torta;
d) Calcule o volume total de filtrado a ser coletado até que os quadros fiquem cheios;
e) Calcule o tempo de filtração total até que os quadros fiquem cheios (considere que tenha sido
utilizado a mesma lona filtrante do experimento apresentado no exercício anterior).
Solução:
a) A = 2 (lados) x 1 (área de 1 lado) x 20 (quadros) = 40 m2
b) Vquadros= 1 (área de 1 lado) x 10-2 (espessura) x 20 (quadros) = 0,2 m3
c) =Vporos/Vtorta= (Vtorta-Vsólidos)/Vtorta=1-Vsólidos/Vtorta
= 1-(m/sólido)/(m /torta) = 1-torta /sólido = 1-1600/2800 = 0,43
d) Vtorta=Vquadros=0,2m3;
mtorta=torta Vtorta= 1600 x 0,2 = 320 kg
V=mtorta/c= 320/23,5=13,6 m3
e) =0Ps=1,4 1010 x (3 105)0,3=6,16 1011 m/kg
Por interpolação: Rm= 2,6 1010 m-1
a= c/(2A2P) = 23,5x6,16 1011x0,886 10-3/(2 x 402 x 3 105)=13,36 s/m6
b=Rm/(AP)= 2,6 1010 0,886 10-3/(40x3 105)=1,92 s/m3
t =aV2+bV=13,36 x 13,62 + 1,92 x 13,6 = 2497 s = 41,6 min
Filtração Contínua
• Aplicados a filtros de tambor rotativo a vácuo;
• Alimentação, o filtrado e a torta se movem com mesma velocidade.
• Resistência do meio filtrante é desprezível, quando comparada a resistência
da torta, logo, Rm pode ser considerado zero.
cs
2
t
V
2
2 A (p)
Para caso particular de um filtro rotatório a vácuo, o tempo t é menor que o
tempo total do ciclo tc:
t = f tc
Onde f é a fração do ciclo usada para formação da torta. No filtro rotatório, f é a
fração submersa da superfície do tambor na suspensão.
Exercício:
Um filtro de tambor rotativo, estando 33% submerso, será usado para a
filtração da suspensão do exercício 1. Calcule a área do filtro necessária para
se obter 0,12 m3 de filtrado por ciclo de filtração, sabendo que:
- Será usada uma queda de pressão de 67 kPa;
- A resistência do meio filtrante pode ser desprezada;
-O tempo de ciclo de filtração é de 250 s.
Solução:
Equação da filtração contínua a pressão constante:
t=cV2/(2A2p)
t=f tc=0,33x250 = 82,5 s
=0Ps=1,4 1010 x (67 103)0,3=3,93 1011 m/kg
A=[cV2/(2tP)]0,5=[0,886 10-3 x 3,93 1011 23,5 x 0,12^2/(2 x 82,5 x 67 103)]0,5
A=3,26 m2
Filtração a velocidade (ou vazão) constante
• Alimentação do filtro é feita por uma bomba de deslocamento positivo.
dV
p

dV
V

 constante
A dt
 csV
 velocidade u 

 Rm 
A dt A t
 A

Sendo:
Rm V
A t
Obtém-se:
 perda de pressão no meio filtrante  Pm
P  Pm  u 2ct
Considerando a seguinte equação empírica para torta compressível:
  0 P  Pm 
s
Obtém-se:
P  Pm 
Linearizando:
1s
 0 u ct
2

logt  1  slogP  Pm   log 0u 2 c

Exercício:
A seguinte tabela apresenta os dados experimentais obtidos em uma filtração a
vazão constante de uma suspensão de MgCO3 em água. A velocidade de
filtração foi de 0,0005 m/s, a viscosidade do filtrado foi de 0,00092 kg/(ms) e a
concentração da suspensão era 17,3 kg/m³. Calcule os parâmetros de filtração
Rm, s e 0.
P(KPa)
30,3
34,5
44,1
51,7
60
70,3
81,4
93,1
104,8
121,3
137,9
t(s)
10
20
30
40
50
60
70
80
90
100
110
Determinação de Pm:
Extrapolando a curva de P versus t,
obtem-se uma estimativa aproximada
de 27 kPa:
Determinação de 0 e s:
160
140
 P (kPa)
120
100
80
60
40
20
0
0
20
40
60
80
100
120
t (s)
Cálculo de Rm:

logt  1  slogP  Pm   log 0u 2 c
Pm
27000
101,3584
10
1
9 m
Rm 

 5,9 10 m  0 

5
,
7

10
u 0,00092 0,0005
0,00092 0,00052 17,3
kg
s  1  0,6757 0,3243
