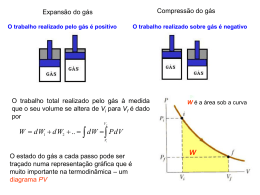
Termodinâmica Aplicada
AULA 6
Fernando Luiz Pellegrini Pessoa
TPQBq
ESCOLA DE QUÍMICA
UNIVERSIDADE FEDERAL DO RIO DE JANEIRO
ESCOLA DE QUIMICA / UFRJ
Termodinâmica Aplicada
Entendendo o Processo de Mistura
As soluções são misturas homogêneas de substâncias químicas,
formadas na natureza ou em processos industriais. Quantidades
específicas de substâncias não-reativas podem ser misturadas
diretamente para formar soluções de composição conhecida. Cada
processo de mistura, em particular, resulta numa mudança de
estado, dependendo das condições inicial e final de temperatura e
pressão. Para facilitar o estudo dos processos de mistura, define-se
o processo padrão de mistura como aquele que ocorre a T e P
constantes. Isto é, quantidades determinadas de substâncias
químicas puras, todas na mesma T e P, são misturadas para formar
uma solução de composição conhecida, também a T e P. Diz-se
que as substâncias puras a T e P estão em seus estados padrão
em relação ao processo de mistura e suas propriedades no estado
padrão são simplesmente as propriedades de substância pura (Vi,
Hi, Si, Gi, ln fi, etc.).
ESCOLA DE QUIMICA / UFRJ
Termodinâmica Aplicada
Processo Padrão de Mistura
No início: quantidades conhecidas de 2 substâncias •
puras (n1 e n2), a T e P, estão separadas por uma
divisória
Divisória
n1
T
P
n2
T
P
ESCOLA DE QUIMICA / UFRJ
P
Termodinâmica Aplicada
Processo Padrão de Mistura
Após a retirada da divisória: o processo de mistura •
começa e, após o tempo necessário e suficiente, formase uma solução (mistura homogênea) de composição
x1 
Divisória
Q
n1 + n 2
Te P
ESCOLA DE QUIMICA / UFRJ
n1
n1  n2
P
Termodinâmica Aplicada
Processo Padrão de Mistura
A observação experimental desse processo de mistura •
permite detectar dois fenômenos:
Ocorre contração ou expansão do volume do sistema, o que se 
verifica pela movimentação do pistão (para que a pressão
mantenha-se constante)
Ocorre transferência de calor entre o sistema e suas 
vizinhanças
ESCOLA DE QUIMICA / UFRJ
Termodinâmica Aplicada
Variação do volume no processo de mistura
A variação do volume total do sistema é calculada por: •
VT  VT  final VT inicial  VT  VT ,1  VT ,2 
VT  n1  n2 V  n1V1  n2V2 
VT  n1  n2 V  n1V1  n2V2
V 
VT
n
 V  x1V1  x2V2
V é a variação de volume por mol da solução, denominada de
VARIAÇÃO DO VOLUME DE MISTURA
ESCOLA DE QUIMICA / UFRJ
Termodinâmica Aplicada
Variação de entalpia no processo de mistura
O calor transferido de/para o sistema ao longo do •
processo de mistura também pode ser medido e, como
o processo ocorre a P constante, esse calor é igual à
variação de entalpia do sistema. Analogamente ao
volume, tem-se que
H  H  x1H1  x2 H 2
onde H é a variação de entalpia de mistura, denominada
simplesmente de CALOR DE MISTURA.
ESCOLA DE QUIMICA / UFRJ
Termodinâmica Aplicada
Variação de propriedade no processo de mistura
Generalizando-se para qualquer propriedade intensiva
da mistura M, tem-se
M  M   xi M i
i
onde M é denominada VARIAÇÃO DE PROPRIEDADE
DE MISTURA
M  f T , P, x 
ESCOLA DE QUIMICA / UFRJ
•
Termodinâmica Aplicada
Representação gráfica da variação de
propriedade de mistura
ESCOLA DE QUIMICA / UFRJ
Termodinâmica Aplicada
Observação
Essa figura mostra que M é a diferença entre a •
propriedade M da solução e uma combinação linear das
propriedades dos componentes puros (x1M1+x2M2). Note
também que, nos limites em que x1=0 ou x1=1, M=0,
pois a propriedade M=M2 e M=M1, respectivamente.
ESCOLA DE QUIMICA / UFRJ
Termodinâmica Aplicada
Solução ideal
O modelo de solução ideal serve como base para •
descrever de forma aproximada o comportamento de
uma solução real .
O modelo de solução ideal fornece a dependência da •
fugacidade dos componentes na solução com a
composição.
Considere o modelo representado pela regra de Lewis- •
Randall:
ˆf id  f (T , P).x
i
i
i
ESCOLA DE QUIMICA / UFRJ
Termodinâmica Aplicada
Mistura de Gases Ideais
A fugacidade de uma espécie i numa mistura de gases •
ideais é dada por:
ˆf  x P  P
i
i
i
Para o gás ideal puro, a T e P, tem-se: •
fi  P
Logo, uma mistura de gases ideais é um caso •
especial de uma solução ideal.
ˆf  x f
i
i i
ESCOLA DE QUIMICA / UFRJ
Termodinâmica Aplicada
Síntese das propriedades e suas
relações para uma solução ideal
(M = ln f, V, Z, H, CP, U ou CV)
M iid  M i
S iid  S i  R ln xi
M iid  0
S iid   R ln xi
M id  0
S id   R xi ln xi
i
Aiid  Ai  RT ln xi
Aiid  RT ln xi
Aid  RT  xi ln xi
M id 
i
S id 
 xi Si  R xi ln xi
i
Aid  RT
i
Giid  Gi  RT ln xi Giid  RT ln xi
G id  RT  xi ln xi
i
ESCOLA DE QUIMICA / UFRJ
 xi M i
G id  RT
i
 xi ln xi   xi Ai
i
i
i
i
 xi ln xi   xi Gi
Termodinâmica Aplicada
Propriedades em Excesso
Propriedade em excesso é a diferença entre o valor de
uma propriedade para uma solução real e o valor da
mesma propriedade para uma solução ideal, nas
mesmas condições de T, P e x.
M E  M  M id
ESCOLA DE QUIMICA / UFRJ
•
Termodinâmica Aplicada
Propriedades em Excesso
ESCOLA DE QUIMICA / UFRJ
Termodinâmica Aplicada
O termo  - xii é definido como uma propriedade de
mistura e tem o símbolo 
=  - xii
ESCOLA DE QUIMICA / UFRJ
Termodinâmica Aplicada
Das quais pode-se deduzir que
As propriedades de mistura foram definidas primeiro
porque H e V podem ser medidas
experimentalmente. Entretanto, as propriedades
em excesso são melhores para análise teórica
ESCOLA DE QUIMICA / UFRJ
Termodinâmica Aplicada
Propriedades em Excesso
Propriedade em excesso é a diferença entre o valor de
uma propriedade para uma solução real e o valor da
mesma propriedade para uma solução ideal, nas
mesmas condições de T, P e x.
M iE  M i  M iid

E

 nM
E
Mi  
 ni
M
E

 M M
M
T ,P ,n
j i
ESCOLA DE QUIMICA / UFRJ
E


i
•
id
E
xi M i
Termodinâmica Aplicada
As propriedades em excesso não •
tem significado para espécies puras,
somente para misturas
ESCOLA DE QUIMICA / UFRJ
Termodinâmica Aplicada
Propriedades em Excesso
Quando M representa as propriedades U, V, H, CP, Cv, Z •
e ln f, tem-se que:
M
E
M iE  M i  M i
 M
E
M i  M i
Essas equações mostram que M iE e ME não representam •
novas funções termodinâmicas, quando M representa as
propriedades U, V, H, CP, Cv, Z e ln f.
ESCOLA DE QUIMICA / UFRJ
Termodinâmica Aplicada
Energia Livre de Gibbs em Excesso
Quando M representar G, A ou S, surgem novas •
funções termodinâmicas.
G E  G  RT
 xi ln xi
___
GiE  Gi  RT ln xi
i
GiE
ln  i 
RT
Gi  RT ln  i
E
E

G

xi ln  i
RT
i
E
G
  ln f
RT
ESCOLA DE QUIMICA / UFRJ
GE 

xi GiE
i
GE
  ln f 
xi ln  i
RT
i

Termodinâmica Aplicada
Energia Livre de Helmholtz e Entropia em Excesso
As mesmas funções termodinâmicas referentes a G se •
aplicam a A, bastando substituir G por A.
A E  A  RT
 xi ln xi
i
___
AiE  Ai  RT ln xi
Para entropia, tem-se as seguintes funções em excesso: •
S E  S  R

i
xi ln xi
___
SiE  Si  R ln xi
ESCOLA DE QUIMICA / UFRJ
Termodinâmica Aplicada
Observação
A correlação das propriedades das soluções usando as
funções em excesso é de grande utilidade devido à
natureza genérica de ME, que pode ser usada para
todas as propriedades consideradas.
M  M E  M id
A única diferença reside no fato de que M  0 para todas
as propriedades , com exceção de G, A e S.
id
ESCOLA DE QUIMICA / UFRJ
Termodinâmica Aplicada
Definindo coeficiente de atividade:
A energia livre de Gibbs determina quais fases
são estáveis. As propriedades em excesso
determinam o coeficiente de atividade, que é
usado para calcular o equilíbrio químico e de
fases para misturas não-ideais. Pode ser
mostrado que:
ESCOLA DE QUIMICA / UFRJ
Termodinâmica Aplicada
Estas equações •
definem o coeficiente
de atividade
ESCOLA DE QUIMICA / UFRJ
Termodinâmica Aplicada
A relação fundamental da propriedade em excesso é
A equação Gibbs- •
Duhem para GE é
ESCOLA DE QUIMICA / UFRJ
Termodinâmica Aplicada
Gi  Gi
id
fˆi
 RT ln
xi f i
G i  RT ln  i
E
A última equação é análoga para
G i  RT ln i
R
P ara solução ideal
G  0.0, então, i  1
E
i
ESCOLA DE QUIMICA / UFRJ
Termodinâmica Aplicada
Relações para as propriedades em excesso
 nGE  nV E
nH E
 
d 
dP 
dT   ln  i dni
2
RT
i
 RT  RT
nV E   ( nG E / RT 

 
RT 
P
T , x
E

nH
 ( nG / RT 

 
RT
T

 P,x
e
E
  ( nG E / RT 

ln  i  
ni

 P ,T ,n j
ESCOLA DE QUIMICA / UFRJ
Termodinâmica Aplicada
Exemplo: A equação de Margules pode ser usada para
correlacionar energia livre de Gibbs. Para uma
mistura binária a expressão de Margules fica:
Encontre ln1 e ln2.
Checar . –
–
Verificar se a Eq. Gibbs-Duhem é satisfeita.
ESCOLA DE QUIMICA / UFRJ
–
Termodinâmica Aplicada
ESCOLA DE QUIMICA / UFRJ
Termodinâmica Aplicada
Checar
ESCOLA DE QUIMICA / UFRJ
Termodinâmica Aplicada
Checar a Eq. Gibbs-Duhem:
ESCOLA DE QUIMICA / UFRJ
Termodinâmica Aplicada
Expressões exatas para o equilíbrio de fases
Quais são as eqs para o EF?
ESCOLA DE QUIMICA / UFRJ
•
Termodinâmica Aplicada
Pode-se colocar em relação da fugacidade ? •
Agora podemos utilizar o coeficiente de
fugacidade no lugar de fugacidade,
ESCOLA DE QUIMICA / UFRJ
•
Termodinâmica Aplicada
Vamos levar em conta o ELV. •
•
é mais conveniente ser utilizado para a fase vapor onde
as EEs são precisas
Para fase líquida é mais convenienete utilizar os coeficientes
de fugacidade, i
Uma expressão exata para o ELV •
ESCOLA DE QUIMICA / UFRJ
•
•
Termodinâmica Aplicada
Simplificação das relações do EF
Esta equação para ELV. É uma boa aproximação para
baixas P. Pode ser simplificada considerando que a
fugacidade do líquido puro é dado por
•
A fase vapor como gás ideal, que é boa aproximação para
P baixas e T menores que a crítica).
Então
•
ESCOLA DE QUIMICA / UFRJ
•
Termodinâmica Aplicada
Desvios da idealidade.
A definição de uma solução ideal diz que as •
propriedades parciais são as mesmas de um
fluido puro. Então para a solução ideal,
Ou, equivalente,
•
Rearranjando, obtem-se a regra de •
Lewis-Randall. A Figura é para uma
solução ideal e com desvios positivos &
negativos da idealidade.
ESCOLA DE QUIMICA / UFRJ
Termodinâmica Aplicada
ESCOLA DE QUIMICA / UFRJ
Termodinâmica Aplicada
A regra de Lewis-Randall e Lei de Henry
A regra de Lewis-Randall é válida para xi  1, mas não é precisa para
xi  0. A Lei de Henry, é precisa para xi  0, mas não é para
xi  1.
•
A regra de Lewis-Randall e a lei de Henry não são
•
independentes, mas estão diretamente relacionadas pela
equação de Gibbs-Duhem. Este fato implica:
Quando a lei de Henry é válida para uma –
espécie em uma mistura binária, então a
regra de Lewis-Randall é válida para a outra
espécie.
ESCOLA DE QUIMICA / UFRJ
•
Termodinâmica Aplicada
ESCOLA DE QUIMICA / UFRJ
Termodinâmica Aplicada
A função de Gibbs e suas principais relações
Gi
RT
 ln  i  ln xi  ln i xi 
ˆf
 i xi  i  aˆ i
fi
Gi
RT
 ln aˆ i
A razão entre as fugacidades é denominada de •
atividade da espécie i na solução.
ESCOLA DE QUIMICA / UFRJ
Termodinâmica Aplicada
Fugacidade de Misturas Gasosas
O critério de equilíbrio entre 2 fases  e , na mesma •
temperatura, é dado pela igualdade das fugacidades de
cada componente i nessas fases:
ˆ ˆ 
fi  fi
Quando uma das fases em equilíbrio é uma mistura
gasosa, tem-se que
ˆf g  y ˆ P
i i
i
•
Para se calcular ˆf i g usando essa equação é necessário •
conhecer o comportamento de ˆ i com P, T e yi, ou seja,
.
ˆi  ˆi P,T , yi 
ESCOLA DE QUIMICA / UFRJ
Termodinâmica Aplicada
Fugacidade de Misturas Gasosas
Considere a fase gasosa monocomponente (substância
pura). A T constante, tem-se que: RTd ln fi  Vi dP
•
RT
dP
Para um gás ideal, essa equação se reduz a: • RTd ln P 
P
Subtraindo-se a segunda equação da primeira, tem-se •
RT 
f  
RTd ln i   Vi 
dP
P 
P 
Integrando-se essa eq. do estado de gás ideal (P=0) até
uma pressão qualquer P, a T constante, chega-se a
P
1 
RT 
 fi 
ln   ln i 
Vi 
dP
RT 
P 
P

0
ESCOLA DE QUIMICA / UFRJ
•
Vi  f T , P
Termodinâmica Aplicada
Fugacidade de Misturas Gasosas
•
A equação anterior pode ser escrita também como
P
 fi 
 Z 1
ln   ln i  
dP
 P 
P

Z
PVi
RT
0
Normalmente, as funções f P, T ,Vi   0 são expressas
na forma explítica em P, ou seja, P  f T ,Vi  . Para esses
casos, essa equação pode ser modificada, passando à
seguinte forma:
1
 fi 
ln   ln i  Z  1  ln Z 
RT
P
ESCOLA DE QUIMICA / UFRJ
V
•

RT 
 P 
dV
Vi 



Termodinâmica Aplicada
Fugacidade de Misturas Gasosas
Por analogia, para o componente i numa mistura, tem-se
que:
P
ˆ
 fi 
1 
RT 
ˆ


ln
 ln i 
Vi 
dP

RT 
P 
 yi P 

•
V  V T , P , n1 , n2 ,
0


 ˆfi 


1

P
RT

dV
  ln ˆi   ln Z 

ln

 n 



y
P
RT
V
i
i




T ,V ,n j
V


P  PT ,V , n1 , n2 ,
ESCOLA DE QUIMICA / UFRJ
Termodinâmica Aplicada
Observação
 P 


 ni T ,V ,n j
não é a propriedade parcial molar de P. Trata-se apenas
de uma simples derivada da função P  PT ,V ,n1 ,n2 , em
relação a ni.
ESCOLA DE QUIMICA / UFRJ
Termodinâmica Aplicada
Observações
As eqs. anteriores são genéricas e relativamente simples.
Porém, obter relações do tipo V  V T , P,n1 ,n2 , e P  PT ,V ,n1 ,n2 ,
depende de modelos que consigam descrever
adequadamente o comportamento PVT dos fluidos. Esses
modelos são as equações de estado. Porém, não existe
uma única equação de estado capaz de calcular
(correlacionar e predizer) as propriedades volumétricas
(PVT) das substâncias puras e das suas misturas para
diversas condições. Há apenas algumas equações de
estado que são boas e úteis para uma classe limitada de
substâncias em certas condições. Essas equações
normalmente são da forma explícita na pressão.
ESCOLA DE QUIMICA / UFRJ