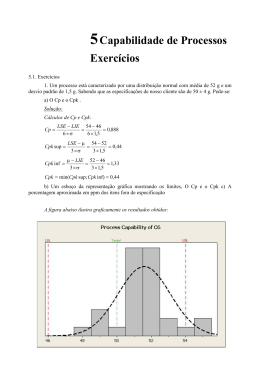
SIMULAÇÃO DE PROCESSOS NA
INDÚSTRIA DE ALIMENTOS
Prof. Paulo Duarte Filho
BAGÉ – SETEMBRO/2010
1. CONTROLE ESTATÍSTICO DE PROCESSOS
Imagine uma planta industrial para a obtenção de
polímeros:
• Engenheiros de alimentos devem projetá-la
para
garantir
produzidos
que
estejam
os
com
polímeros
as
por
ela
características
desejadas pelos clientes;
• Para verificar se está tudo conforme planejado,
os engenheiros acompanham sistematicamente
as características do polímero que está sendo
produzido;
1. CONTROLE ESTATÍSTICO DE PROCESSOS
• Foi avaliado o parâmetro viscosidade para o
controle da produção;
• Então, de tempos em tempos foram coletados
uma amostra na saída da linha de produção e
enviada ao laboratório para a determinação de
sua viscosidade;
• Todos os valores são plotados em um gráfico
em função do tempo;
1. CONTROLE ESTATÍSTICO DE PROCESSOS
• Se o processe estiver totalmente sob controle,
sem erros grosseiros nem sistemáticos, como
deve ser a distribuição desses pontos???
• Quando o processo está sob controle, sua
variabilidade
é
devida
apenas
aos
erros
aleatórios.
PRINCÍPIO BÁSICO DO CONTROLE DE QUALIDADE
1. CONTROLE ESTATÍSTICO DE PROCESSOS
• Exemplo de um gráfico de dispersão
1. CONTROLE ESTATÍSTICO DE PROCESSOS
• Distribuição normal – Histograma
SITUAÇÃO IDEAL – “SONHO DE TODO O ENGENHEIRO DE ALIMENTOS”
1. CONTROLE ESTATÍSTICO DE PROCESSOS
• As
cartas
ou
mapas
controle
são
uma
ferramenta fundamental para a detecção de
problemas que possam estar perturbando o
processo;
• Qualquer padrão anômalo, que indique desvios
da normalidade, é um aviso de que os
responsáveis devem tomar as providências
necessárias para fazer o processo voltar ao
controle;
1. CONTROLE ESTATÍSTICO DE PROCESSOS
• Como pode se observar a carta controle é
composto por três linhas horizontais paralelas;
Limite superior de controle
Média
Limite inferior de controle
1. CONTROLE ESTATÍSTICO DE PROCESSOS
• Situações
anômalas:
Como
identificá-las?
Conhecimento técnico do funcionamento da
planta, bem como nas evidências obtidas a partir
do gráfico;
1. CONTROLE ESTATÍSTICO DE PROCESSOS
• Existem algumas regras práticas para auxiliar
os operadores a detectar situações anômalas:
 um ou mais pontos localizados fora dos
limites de controle;
 quatro pontos, de cinco sucessivos,
situados a mais de um desvio padrão da
média, de um mesmo lado da linha
central;
1. CONTROLE ESTATÍSTICO DE PROCESSOS
• Existem algumas regras práticas para auxiliar
os operadores a detectar situações anômalas:
seis pontos consecutivos ascendentes
ou descendentes;
 nove pontos sucessivos de um mesmo
lado da linha central.
1. CONTROLE ESTATÍSTICO DE PROCESSOS
Qualidade:
Definida pela satisfação do cliente.
Ex:
Vamos
supor
que
um
fabricante
de
embalagens diz a um fabricante de biopolímeros
que só compra seu produto se ele tiver uma
viscosidade de 45 cp. No entanto, tendo em vista
as dificuldades, o fabricante de embalagens está
disposto a aceitar uma variação de 3 unidades
para mais ou para menos na viscosidade.
1. CONTROLE ESTATÍSTICO DE PROCESSOS
Ex: Sendo assim, tem-se os valores definidos
para os limites de tolerância da especificação: 42
(mínimo)
e
48
(máximo).
Os
lotes
de
biopolímeros que caírem fora da faixa de
tolerância serão rejeitados e imediatamente
devolvidos ao fornecedor.
1. CONTROLE ESTATÍSTICO DE PROCESSOS
Mesmo que o fornecedor tenha seu processo sob
controle, isso não quer dizer que o produto irá
satisfazer obrigatoriamente às especificações. É
necessário também comparar os parâmetros de
controle com os parâmetros de especificação.
MEDIDA DA CAPACIDADE DO PROCESSO!!!!
1. CONTROLE ESTATÍSTICO DE PROCESSOS
Um dos índices de capacidade mais utilizados é o
Cpk. É definido como a menor das duas frações:
LSE – μ / 3σ
μ – LIE / 3σ
LSE = limite superior de especificação;
LIE = Limite inferior de especificação;
μ = estimativa confiável da média;
σ = estimativa confiável do desvio padrão
1. CONTROLE ESTATÍSTICO DE PROCESSOS
Ex: Se o cliente deseja um biopolímero com
viscosidade entre 42 e 48, e o processo está
operando com μ = 46 e σ = 1,6. Calcule o Cpk.
0,42 e 0,83. Utiliza-se o menor valor obtido das
duas frações.
Portanto, Cpk= 0,42 - Péssimo
1. CONTROLE ESTATÍSTICO DE PROCESSOS
Avaliação do cálculo do índice:
• Processo incapaz: Cpk < 1;
• Processo aceitável : 1,0 ≤ Cpk ≤ 1,33;
• Processo capaz: Cpk ≥ 1,33.
“A Motorola e a general Eletric já estabeleceram
Cpk igual a 2 como padrão mínimo de qualidade
para
seus
fornecedores”.
processos,
bem
como
seus
1. CONTROLE ESTATÍSTICO DE PROCESSOS
Cpk baixo
Causa: a distribuição está centrada, mas há uma
variação maior que a faixa dos limites de especificação
Processo: incapaz
Cpk bom
Causa a distribuição está centrada e há uma variação
menor que a faixa dos limites de especificação
Processo: satisfatório
Cpk alto
Causa: a distribuição está centrada e há uma baixa
variação em relação à faixa dos limites de especificação
Processo: capaz
2. ANÁLISE DE VARIÂNCIA
O objetivo principal da análise de variância é
comparara variação devida aos tratamentos (ex:
concentração de nutrientes) com a variação devida ao
acaso ou resíduo. Para realizá-la é preciso proceder a
uma série de cálculos.
2. ANÁLISE DE VARIÂNCIA
Os seguintes cálculos são necessários para a
realização da análise de variância:
a) Graus de liberdade:
• de tratamentos: k – 1
• do total: n – 1, com n = k.r
• do resíduo: (n – 1) – (k – 1) = n - k
2. ANÁLISE DE VARIÂNCIA
b) O valor C, dado pelo total geral elevado ao
quadrado e dividido pelo número de observações.
O valor C é conhecido como correção:
C = (Σy)2 / n
c) A soma de quadrados total:
SQT = Σy2 – C
d) A soma de quadrados de tratamentos:
SQTr = ΣT2 / r - C
2. ANÁLISE DE VARIÂNCIA
e) A soma de quadrados de resíduo:
SQR = SQT – SQTr
f) O quadrado médio de tratamentos:
QMTr = SQTr / K – 1
g) O quadrado médio de resíduo:
QMR = SQR / n – k
h) O valor de F
F = QMTr / QMR
2. ANÁLISE DE VARIÂNCIA
Exercício: Faça a análise de variância para o
experimento
abaixo.
Comente
os
resultados
obtidos.
Produção de milho em Kg / 100 m2 segundo a variedade
Variedade
A
B
C
D
25
31
22
33
26
25
26
29
20
28
28
31
23
27
25
34
21
24
29
28
2. ANÁLISE DE VARIÂNCIA
Utilizando o Excel:
Anova: fator único
RESUMO
Grupo
Contagem
Soma
Média
Variância
Coluna 1
5
115
23
6,5
Coluna 2
5
135
27
7,5
Coluna 3
5
130
26
7,5
Coluna 4
5
155
31
6,5
ANOVA
Fonte da variação
Entre grupos
Dentro dos grupos
Total
SQ
gl
MQ
F
163,75
3
54,58333
112
16
7
275,75
19
7,797619
valor-P
F crítico
0,001976
3,238872
2. ANÁLISE DE VARIÂNCIA
Utilizando o Excel:
Coluna1
Coluna2
Coluna3
Coluna4
Média
23 Média
27 Média
26 Média
31
Erro padrão1,140175 Erro padrão1,224745 Erro padrão1,224745 Erro padrão1,140175
Mediana
23 Mediana
27 Mediana
26 Mediana
31
Desvio padrão
2,54951 Desvio padrão
2,738613 Desvio padrão
2,738613 Desvio padrão
2,54951
Variância da amostra
6,5 Variância da amostra
7,5 Variância da amostra
7,5 Variância da amostra
6,5
Curtose
-2,26036 Curtose
-0,13333 Curtose
-0,13333 Curtose
-2,26036
Assimetria 6,94E-17 Assimetria 0,608581 Assimetria -0,60858 Assimetria
0
Intervalo
6 Intervalo
7 Intervalo
7 Intervalo
6
Mínimo
20 Mínimo
24 Mínimo
22 Mínimo
28
Máximo
26 Máximo
31 Máximo
29 Máximo
34
Soma
115 Soma
135 Soma
130 Soma
155
Contagem
5 Contagem
5 Contagem
5 Contagem
5
Nível de confiança(95,0%)
3,165634 Nível de confiança(95,0%)
3,400437 Nível de confiança(95,0%)
3,400437 Nível de confiança(95,0%)
3,165634