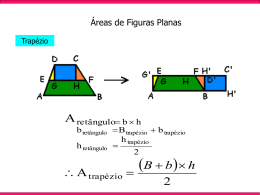
Provas do Enem
Geometria Plana
Questões adaptadas de provas do Enem de anos anteriores
O tangram é um jogo oriental antigo, uma espécie
de quebra-cabeça, constituído de sete peças: 5 triângulos
retângulos e isósceles, 1 paralelogramo e 1 quadrado.
Essas peças são obtidas recortando-se um quadrado de
acordo com o esquema da figura 1. Utilizando-se todas as
sete peças, é possível representar uma grande diversidade
de formas, como as exemplificadas nas figuras 2 e 3.
Figura 1
Figura 2
Se o lado AB do hexágono mostrado na figura 2 mede
2 cm, então a área da figura 3, que representa uma
“casinha”, é igual a
A) 4 cm².
B) 8 cm².
C) 12 cm².
D) 14 cm².
E) 16 cm².
Figura 3
Paralelogramo: polígono de 4 lados com lados opostos iguais e paralelos.
Há 3 casos especiais:
a) Retângulo: quatro ângulos retos. O ângulo reto vale 90 graus (90°).
b) Quadrado: quatro ângulos retos e quatro lados iguais (é um caso particular do
retângulo).
c) Losango: quatro lados iguais e ângulos opostos iguais. Se os 4 ângulos forem iguais
entre si, trata-se de um quadrado.
Perímetro é a soma de todos os lados.
Diagonal é um segmento de reta que
une vértices não consecutivos.
Área representa a região ocupada pelo
polígono no plano.
Triângulo é uma figura geométrica fechada composta por 3
lados e 3 ângulos. Podem ser:
a) Escaleno: os 3 ângulos e os 3 lados possuem valores
diferentes.
b) Isósceles: possui 2 lados com mesma medida 2 ângulos
iguais.
c) Equilátero: possui os 3 lados e os 3 ângulos com
medidas iguais.
A soma dos ângulos internos de
um triângulo vale 180 graus (180°).
Resposta: B
A vazão do rio Tietê, em São Paulo, constitui
preocupação constante nos períodos chuvosos. Em alguns
trechos, são construídas canaletas para controlar o fluxo
de água. Uma dessas canaletas, cujo corte vertical
determina a forma de um trapézio isósceles, tem as
medidas especificadas na figura I. Neste caso, a vazão da
água é de 1.050 m3/s. O cálculo da vazão, Q em m3/s,
envolve o produto da área A do setor transversal (por onde
passa a água), em m2, pela velocidade da água no local, v,
em m/s, ou seja, Q = Av.
Planeja-se uma reforma na canaleta, com as
dimensões especificadas na figura II, para evitar a
ocorrência de enchentes.
Na suposição de que a velocidade da água não se
alterará, qual a vazão esperada para depois da reforma na
canaleta?
A) 90 m³/s.
B) 750 m³/s.
C) 1.050 m³/s.
D) 1.512 m³/s.
E) 2.009 m³/s.
Trapézio: quadrilátero (figura com 4 lados) que possui 2 lados paralelos entre si.
Estes lados são as bases do trapézio: base menor (b) e base maior (B).
Resposta: D
O governo cedeu terrenos para que famílias
construíssem suas residências com a condição
de que no mínimo 94% da área do terreno
fosse mantida como área de preservação
ambiental. Ao receber o terreno retangular
ABCD, em que AB = BC/2, Antônio demarcou
uma área quadrada no vértice A, para a
construção de sua residência, de acordo com o
desenho, no qual AE = AB/5 é lado do
quadrado.
Nesse caso, a área definida por Antônio atingiria
exatamente o limite determinado pela condição se
ele:
A) duplicasse a medida do lado do quadrado.
B) triplicasse a medida do lado do quadrado.
C) triplicasse a área do quadrado.
D) ampliasse a medida do lado do quadrado em 4%.
E) ampliasse a área do quadrado em 4%.
10x
5x
x
x
A  10 x.5 x  50 x²
a  x.x  x²
A  100 %
a  2%
Mas o limite referido na
questão é de 6%. Logo,
para se atingir este limite,
deve-se triplicar a área “a”.
Resposta: C
Um município de 628 km² é
atendido por duas emissoras
de rádio cujas antenas A e B
alcançam um raio de 10km do
município, conforme mostra a
figura:
Para orçar um contrato publicitário,
uma agência precisa avaliar a
probabilidade que um morador tem de,
circulando livremente pelo município,
encontrar-se na área de alcance de pelo
menos uma das emissoras.Essa
probabilidade é de aproximadamente:
(A) 20%.
(B) 25%.
(C) 30%.
(D) 35%.
(E) 40%.
Comprimento da circunferência:
C=2πr
sendo r o raio.
Área da circunferência:
A = π r²
A probabilidade citada no
exercício é igual à soma das
áreas circulares dividido
pela área total.
P = Ac /At
Resposta: B
Resposta: E
Resposta: D
Na literatura de cordel, os textos são impressos, em geral, com 8, 16, 24 ou 32 páginas de formato 10,5 cm x 15,5
cm. As razões históricas que explicam tal fato estão relacionadas à forma artesanal como são montadas as
publicações e ao melhor aproveitamento possível do papel disponível.
Considere, abaixo, a confecção de um texto de cordel com 8 páginas (4 folhas):
Utilizando o processo descrito acima, pode-se produzir um exemplar de cordel com 32 páginas de 10,5 cm x 15,5
cm, com o menor gasto possível de material, utilizando uma única folha de
(A) 84 cm x 62 cm
(B) 84 cm x 124 cm
(C) 42 cm x 31 cm
(D) 42 cm x 62 cm
(E) 21 cm x 31 cm
Resposta:D
A sombra de uma pessoa que tem
1,80 m de altura mede 60 cm. No
mesmo momento, a seu lado, a
sombra projetada de um poste mede
2,00 m. Se, mais tarde, a sombra do
poste diminuiu 50 cm, a sombra da
pessoa passou a medir:
(A) 30 cm
(B) 45 cm
(C) 50 cm
(D) 80 cm
(E) 90 cm
h
1,80m
0,60m
2m
h
1,80m
x
1,50m
Os triângulos são semelhantes,
pois possuem os três ângulos
iguais. Logo:
h 1,80

2 0,60
h  6,0m
6,0m
1,80m
x
1,50m
6 1,80

1,5
x
x  0,45m
x  45cm
Resposta: B
A rampa de um hospital tem na sua
parte mais elevada uma altura de 2,2
metros. Um paciente ao caminhar sobre
a rampa percebe que se deslocou 3,2
metros e alcançou uma altura de 0,8
metro. A distância em metros que o
paciente ainda deve caminhar para
atingir o ponto mais alto da rampa é:
A) 1,16 metros
B) 3,0 metros.
C) 5,4 metros.
D) 5,6 metros.
E) 7,04 metros.
2,2m
0,8m
Os triângulos são semelhantes,
pois possuem os três ângulos
iguais. Logo:
0,8
2,2

3,2 3,2  x
x  5,6m
Em uma empresa, existe um galpão que
precisa ser dividido em três depósitos e
um hall de entrada de 20 m², conforme a
figura abaixo. Os depósitos I, II e III serão
construídos para o armazenamento de,
respectivamente, 90, 60 e 120 fardos de
igual volume, e suas áreas devem ser
proporcionais a essas capacidades.
A largura do depósito III dever
ser, em metros, igual a:
(A) 1. (B) 2. (C) 3. (D) 4.(E) 5.