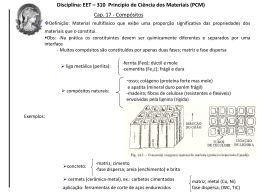
COMPÓSITOS
• Formados por dois
materiais a nível
macroscópico
• Enorme gama de
propriedades
• Excelentes rigidez e
resistência específicas
• Fibras e matriz cerâmicas
resistem a altas
temperaturas
TIPOS DE MATERIAIS COMPÓSITOS
REFORÇADOS
C/PARTÍCULAS
REFORÇADOS
C/ FIBRAS
COMPÓSITOS
LAMINARES
• Concreto
• Fibras de
carbono,
Kevlar, vidro,
etc
• Laminados
de fibras e
resina
• Asfalto
• Cermet
• Sandwich
• Matriz de
epoxy,
poliéster,
PEEK, etc
COMPÓSITOS
NATURAIS
• Madeira
A Fase Fibra
PROPRIEDADES DAS FIBRAS
Devem usar-se fibras com
grandes resistência e rigidez
específicas.
CONTROLE DE PROPRIEDADES
PROPRIEDADES DA MATRIZ
LIGAÇÃO FIBRA-MATRIZ
Matrizes poliméricas têm em
geral baixa resistência e baixo
ponto de fusão
Se não houver boa aderência da
matriz à fibra, não há distribuição
de esforços eficiente
Matrizes metálicas têm maior
resistência e maior ponto de
fusão, mas são mais pesadas
O coeficiente de expansão
térmica deve ser muito
semelhante entre fibras e matriz
Podem ser usadas matrizes
cerâmicas para resistência a
temperaturas extremamente
elevadas, perdendo-se
tenacidade
FRAÇÃO EM VOLUME DE FIBRAS
Quanto maior for este valor, maior será a resistência do compósito,
até um valor limite de 80%, a partir do qual deixa de haver
“molhagem” total das fibras pela matriz.
(a) Fraca aderência entre as fibras e a matriz
(b) Excelente aderência entre fibras e matriz
COMPÓSITOS AVANÇADOS
COMPÓSITOS DE MATRIZ
METÁLICA
Podem ser usados a
temperaturas superiores em
relação aos compósitos de
matriz polimérica
Possuem maior resistência
mecânica que o metal da
matriz não reforçado
Atenua-se a vantagem das
maiores resistência e rigidez
específicas
COMPÓSITOS AVANÇADOS
• COMPÓSITOS CERÂMICA-CERÂMICA
 Possuem uma maior tenacidade à fratura em relação ao cerâmico não
reforçado;
 Usados apenas em aplicações de elevada temperatura (+ 1000ºC)
Comparação entre as resistências específicas de materiais
compósitos e não compósitos.
Compósitos Reforçados com Partículas
A resistência mecânica é fortemente dependente da ligação entre as
partículas e a matriz, sendo por isso difícil de prever teoricamente !
COMP .  V f  f Vmm
Módulo de elasticidade
deve estar entre os limites
superior e inferior
Ec (u) = EmVm + EpVp
Limite superior
Ec (l) = EmEp/(VmEp + VpEm)
Limite inferior
Compósitos Reforçados com Fibras
Faz-se uso de compósitos reforçados com fibras em projetos cujos
objetivos incluem uma alta relação resistência/peso.
 Influência do comprimento da fibra: quando uma tensão é
aplicada em um compósito deste tipo a ligação matriz-fibra cessa
nas extremidades da fibra.
 Comprimento crítico: comprimento de fibra mínimo, necessário
para que haja um efetivo aumento da resistência do compósito.
Lc = σfd/2tc
Compósitos Reforçados com Fibras
 Perfis tensão-posição em função do comprimento da fibra (l) e o
seu comprimento crítico (lc):
Alguns arranjos típicos
de fibras em cada
camada de compósito
a) Fibras unidirecionais
contínuas
b) Fibras descontínuas
orientadas de modo
aleatório
c) Fibras unidirecionais
tecidas ortogonalmente
Comportamento Elástico em Função da Direção de Carregamento
ORIENTAÇÃO DAS FIBRAS
A resistência será máxima
quando as fibras estiverem
orientadas com o esforço
(sendo mínima na direção
perpendicular)
Variação de propriedades com a
orientação das fibras para uma liga de
Titânio reforçada com fibras de Boro
Comportamento Elástico em Função da Direção de Carregamento
Para uma carga alinhada na direção do carregamento:
Ecl = EmVm + EfVf
módulo de elasticidade do compósito
Ecl = Em (1-Vf) + EfVf
Ff/Fm = EfVf/EmVm
relação entre a carga suportada pelas fibras e pela matriz
Para uma carga alinhada na direção transversal ao carregamento:
1/Ecl = Vm/Em + Vf/Ef
módulo de elasticidade do compósito
Ecl = Em Ef / VmEf + VfEm = EmEf/ (1-Vf)+ VfEm
Ff/Fm = EfVf/EmVm
relação entre a carga suportada pelas fibras e pela matriz
• Regra das misturas: usada quando para compósitos com fibras descontínuas e
aleatoriamente orientadas:
Ecd = Vm/Em + KVf/Ef
Resistência longitudinal do compósito
• Para εf < εm em compósitos com fibras contínuas e alinhadas:
σcl = σm (1+Vf) + σfVf
σm = tensão na matriz no momento em que ocorre a falha da
fibra;
σf = limite de resistência à tração da fibra.
 Para compósitos com fibras descontínuas e alinhadas:
• Para l > lc :
σcd = σfVf (1- lc/2l) + σm(1-Vf)
• Para l < lc
σcd = ltcVf/d + σm(1-Vf)
:
COMPÓSITOS DE MATRIZ POLIMÉRICA
MATRIZ
Termoplásticos
PET
PP
etc
Termoendurec.
EP, PF
PEEK
etc
REFORÇO
Fibras
Fibras
plásticas Carbono
Fibras
Cerâmicos Metais
Vidro
PP
Aramid
E
S
HM
HS
SiC
Al2O3
B
Arame
MATRIZ DO COMPÓSITO
REFORÇO DO COMPÓSITO
Transmite os esforços mecânicos
aos reforços (fibras), mantendoos em posição, e contribuindo
com alguma ductilidade (em geral
pequena) para o compósito.
Elemento que suporta os
esforços no compósito. É, em
geral, de elevadas resistência e
rigidez.
Compósitos com matriz polimérica
a) Aderência ruim entre a matriz e as fibras;
b) Boa aderência entre a matriz e as fibras