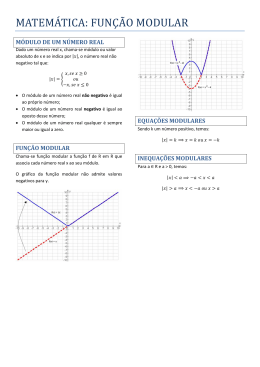
Função Modular: Análise de Livros Didáticos Segundo a Teoria
dos Registros de Representação Semiótica
Andrea Priscila Luiz dos Santos1,
Silmara Alexandra da Silva Vicente2
Área do Conhecimento: Ciências Humanas.
Palavras-chaves: Registros de Representação Semiótica; Livros Didáticos; Função modular.
INTRODUÇÃO
Duval (2003), pesquisador da área de Educação
Matemática aponta a importância de se analisar o papel
das diversas representações quando se considera um
objeto matemático. Um grande problema que ocorre na
aprendizagem de conceitos matemáticos decorre do fato de
que não é possível acessá-los por meio de um instrumento
ou mesmo pela percepção. Desta forma, para se explorar
um objeto matemático, é necessária a utilização de um
sistema semiótico ou registro de representação como, por
exemplo, os registros algébricos, numéricos e gráficos.
Este pesquisador ainda expõe que, no ensino de
Matemática, não há preocupação na exploração das diversas
representações de um conceito e que, principalmente nos
níveis mais avançados do ensino, há um “enclausuramento”
de registro.
Este fato pode desencadear diversas dificuldades
para os estudantes, dentre elas a identificação de um objeto
matemático com uma única representação ou a conclusão
inadequada de que duas representações do mesmo ente
matemático representam objetos distintos. Exemplificando:
o conteúdo de um gráfico de uma função não é o mesmo
que o de sua expressão algébrica, apesar de denotarem o
mesmo objeto matemático.
“Sempre que um sistema semiótico
é alterado, o conteúdo da representação
muda, enquanto o objeto denotado permanece
o mesmo. Mas como objetos matemáticos não
podem ser identificados com alguma de suas
representações, vários estudantes não podem
discriminar o conteúdo da representação e
o objeto representado...” (DUVAL, 2000,
p.59).
Tal problemática aponta a necessidade de uma
abordagem de ensino que estabeleça uma coordenação
consciente da variedade de representações de um conceito
matemático. Esse autor mostra que há dois tipos de
operação possíveis entre os registros: o tratamento e a
conversão. Enquanto o tratamento é a operação realizada
no interior de um mesmo registro semiótico, a conversão
envolve uma transformação entre representações
provenientes de registros distintos. É o caso, por exemplo,
de construir um gráfico a partir de uma função dada na
sua representação algébrica. É na atividade de conversão
que se exige um maior esforço cognitivo, principalmente
quando a transformação não é congruente, ou seja, quando
a passagem de uma representação para outra não se faz de
maneira direta.
OBJETIVOS
O objetivo do projeto consistiu em realizar um
estudo de dois livros didáticos, indicados no Parâmetro
Curricular Nacional – PCN, especificamente com relação
ao conteúdo de função modular, com foco na teoria dos
registros de representação semiótica de Duval (2000, 2003,
2006), evidenciando as representações mais presentes e as
conversões mais requeridas.
METODOLOGIA
A metodologia de pesquisa consistiu no
cumprimento das seguintes etapas:
a) Primeiramente, foi realizado um estudo das
pesquisas que embasaram o tema desenvolvido nesse
trabalho, com isso foi realizada uma revisão bibliográfica;
modular;
b) Foi necessário o estudo do conteúdo de função
c) Análise do conteúdo de função modular de duas
Estudante do Curso de Licenciatura em Matemática; e-mail: andrea_prg@
hotmail.com1
Professor da Universidade Bandeirante de São Paulo; e-mail: silalevicente@
gmail.com2
--
obras da primeira série do ensino médio (obras indicadas e
bem avaliadas pelos Parâmetros Curriculares Nacionais),
com foco na teoria dos registros de representação
semiótica;
d) Foi elaborada uma proposta de abordagem
de função modular, evidenciando os objetivos, as
representações e conversões presentes;
e) Para finalização, foi elaborado o relatório final
do projeto.
RESULTADOS E DISCUSSÃO
Análise dos Livros Didáticos
Faremos a análise de cada livro que serão
identificados como livro 1 e livro 2, com o objetivo
de apontar os pontos comuns, a maneira como é feita
abordagem do conteúdo e seu desenvolvimento quanto às
transformações de um registro a outro.
o intervalo de soluções de forma geral. Com todas estas
informações, a autora volta aos dois problemas iniciais
e mostra a resolução algébrica através da inequação que
traz o intervalo de resolução do mesmo, ou seja, mais uma
mudança de registro para resolução do problema.
Nos exercícios resolvidos, dos quatro, somente
o último apresenta uma mudança de registro, do algébrico
para a reta real, ou seja, uma conversão congruente onde
há uma simples codificação em encontrar o intervalo em
que a solução se encontra e destacar corretamente na reta
real.
Vamos acompanhar a resolução do exercício 2
sem mudança de registro:
O enunciado pede para resolver a equação
2
2x −5x −3= 0
Livro 1 – Smole (2006)
Parte teórica
A autora inicia o capítulo definindo o que é
módulo de um número real para depois exemplificar a
função modular, com os seguintes problemas:
O primeiro problema é identificar o valor real
das intenções de votos de um candidato em porcentagem
no decorrer do tempo em meses, através de um gráfico e
em uma reta numérica.
Esse é um tipo de exemplo que trata de uma
informação rotineira em época de eleição que presenciamos
em noticiários, jornais e revistas. Contudo, muitas vezes
o cidadão não sabe interpretar os dados ali obtidos nos
gráficos e/ou tabelas.
O segundo problema é calcular os diâmetros de
moléculas que têm como unidade de medida o nanômetro
(nm), através do auxílio de um microscópio eletrônico
que fornece o valor médio do objeto de estudo, neste caso
representado somente na reta numérica.
Ambos apresentam na reta o ponto médio num
intervalo de dois pontos percentuais de erro tanto para
mais quanto para menos. O desenvolvimento de qualquer
conhecimento quando abrange representações diferentes
torna o aprendizado mais rico e prazeroso facilitando uma
apropriação maior do conteúdo trabalhado.
O conteúdo prossegue com registro na língua
natural com a definição e um sistema de escrita simbólico
especial. Os exemplos numéricos e algébricos são
destacados para apresentar as propriedades do módulo na
reta numérica. Numa comparação de números opostos, a
autora aproveita para introduzir o conceito de inequação
com símbolos de maior-igual, menor-igual mostrando
Análise dos Exercícios Propostos
Os exercícios propostos de módulo de um
número têm um nível bom de dificuldade, propõe questões
mais fáceis com linguagem numérica e gradativamente
desenvolve a linguagem algébrica trabalhando sentenças
em verdadeiro ou falso, expressões, equações e inequações
modulares com representações na reta real. Há um
total de nove exercícios para analisar seus registros de
representações semióticas:
Exercício
1.
2.
3.
4.
5.
6.
7.
8.
9.
Enunciado
Sistema de escrita
numérica
Sistema de escrita
algébrico numérico
Sistema de escrita
simbólico
Sistema de escrita
algébrico
Sistema de escrita
algébrico numérico
Sistema de escrita
símbolo algébrico
Sistema de escrita
símbolo algébrico
Sistema de escrita
algébrico numérico
Sistema de escrita
algébrico numérico
Resolução
(tratamento)
Resolução
(Conversão)
Numérico
Não há conversão
Algébriconumérico
Não há conversão
Simbólico
Não há conversão
Algébrico
Não há conversão
Algébriconumérico
Não há conversão
Reta real
Há conversão
congruente
Algébrico
numérico
Algébrico
numérico
Algébrico
numérico
Não há conversão
Não há conversão
Não há conversão
--
Podemos observar que destes exercícios
propostos somente o sexto exercício tem mudança de
registro, ou seja, uma conversão congruente. Pelo fato
de mudar a representação algébrica para a reta real é
considerado congruente, pois sua codificação é simples.
Esta conversão congruente deixa de ter uma
codificação simples na abordagem da função modular, até
mesmo porque existe certa complexidade ao se aprofundar
no assunto.
Depois de ter a definição de módulo e o que é
uma função, é possível descrever a função modular, que
abrange vários conhecimentos como: inequação, bissetriz,
simetria e ângulo relacionados aos quadrantes do gráfico.
Suas respostas apresentam o domínio e a imagem das
respectivas funções.
Livro 2 – Dante(2006)
Módulo de um número real
Parte teórica
O autor inicia também o capítulo com o módulo
de um número real, exemplos na língua natural, numéricos,
algébricos e geométricos com estudos de sinais a partir da
raiz (ou zero da função) para identificar a solução, que na
reta real indica a distância de um número ao zero.
O módulo de um número qualquer é sempre
positivo ou zero, são quatro exemplos diferentes para
abordar o maior número de casos possíveis. No entanto
o registro mais trabalhado até o momento é o sistema de
escrita algébrico-numérico.
Exemplo:
O autor propõe dois exercícios e tem a preocupação
de apresentar, em seguida, cinco propriedades envolvendo
módulo, porém sem demonstrações. Utiliza a linguagem
algébrica e numérica e mais três exercícios propostos nos
quais não há mudanças de registro, permanece no mesmo
tratamento.
A partir desse desenvolvimento, o autor
apresenta uma mudança de registro utilizando a reta real
para determinar a distância entre dois pontos através do
módulo, fazendo correspondência entre os pontos da reta
e os números reais. Da introdução de módulo temos no
total sete exercícios propostos sendo que somente os dois
últimos teriam uma mudança de registro, mas o sexto
exercício é o único que trabalho com a reta real como dados
para resolução do problema, uma conversão congruente de
codificação simples.
CONCLUSÕES
Essa pesquisa de Iniciação Científica mostrou que
a teoria de Duval, que trata dos registros de representações
semióticas, é importante e contribui para favorecer uma
melhor aprendizagem. Nesse trabalho esta teoria foi
utilizada na análise de dois livros didáticos que atualmente
são empregados nas aulas do ensino médio.
Atualmente, o conteúdo de função modular tem
sido trabalhado apenas no Ensino Superior nos cursos da
área de exatas. Entretanto, não se justifica o caráter opcional
com o qual esse conteúdo é tratado no Ensino Médio
chegando a ser considerado é dispensável, pois o conceito
é básico e fundamental devendo ser bem desenvolvido,
com a exploração de exemplos e exercícios em sala de
aulas. Esse conceito é utilizado em Cálculo Diferencial e
Integral I, Física, entre outros.
Em geral, os dois livros trabalham de forma
semelhante o conteúdo e os exercícios de função modular.
O livro do Dante (2005) apresenta mais conteúdo e
propriedades desse tipo de funçã. Esperava-se que esse
livro trouxesse informações mais resumidas por se tratar
de volume único. Ao se comparar esse livro com outros
livros didáticos de volume único é notória a diferença, pois
em alguns esse conteúdo não é apresentado, e nesse livro o
autor propõe praticamente o mesmo número de exemplos,
exercícios resolvidos e exercícios propostos, tornando o
assunto bem explorado.
O livro didático da Smole (2005) apresenta um
capítulo inteiro de função modular e propõe somente cinco
exercícios que desenvolvem registros de conversão, quando
todos os exercícios poderiam ser desenvolvidos com mais
de dois registros, principalmente tabelas e gráficos. O
livro didático da Smole (2005) não é volume único e ainda
assim não explora os exercícios trabalhando as conversões
de registros de representação semiótica.
--
REFERÊNCIAS BIBLIOGRÁFICAS
DANTE, L.R. Matemática. Ática, 2006.
DUVAL, R. Registros de representações
semióticas e funcionamento cognitivo da compreensão
em Matemática. In: MACHADO, S.D.A. Aprendizagem
em Matemática: Registros de representação semiótica.
Campinas: Papirus, 2003. p. 11-33.
SMOLE, K.C.S.; KIYKAWA, R. DINIZ,
M.I.S.V. Matemática - Ensino Médio Saraiva, 2006.
--