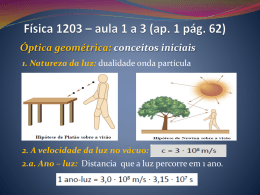
Séries
Consideremos uma sequência de termo geral an . A partir dos termos desta sequência formamos uma nova
sequência de termo geral sk , onde
s1 = a1
s2 = a1 + a2
s3 = a1 + a2 + a3
...
P
sk = a1 + a2 · · · ak = kn=1 an .
Se a sequência (sk ) tem limite s quando k tende para o infinito, dizemos que a série
e
k
∞
X
X
s = lim sk = lim
an =
an .
k→∞
k→∞
n=1
P∞
n=1 an
é convergente
n=1
P∞
A sequência (sk ) é chamada soma
parcial
da
série
n=1 an . E se (sk ) não tem limite quando k tende para
P∞
o infinito, dizemos que a série n=1 an é divergente.
Exemplos: A série geométrica
∞
X
aq n−1 = a + aq + aq 2 + · · ·
n=1
é convergente se |q| < 1 e sua soma é
∞
X
aq n−1 =
n=1
a
1−q
|q| < 1.
Se |q| ≥ 1, a série geométrica é divergente.
Exemplos: A série harmônica
∞
X
1
1 1 1
= 1 + + + ···
n
2 3 4
n=1
é divergente.
Teorema: Se a série
P∞
n=1 an
for convergente, então limn→∞ an = 0.
O Critério para
P∞ Divergência (ou Critério do termo geral): Se limn→∞ an não existir ou se limn→∞ an 6= 0,
então a série n=1 an é divergente.
Critério da Integral:
R ∞ em [1, ∞) e seja an =
P∞Suponha que f seja uma função contı́nua, positiva e decrescente
f (n). Então a série n=1 an é convergente se e somente se a integral imprópria 1 f (x)dx for convergente.
Em outra palavras:
∞
Z
i. Se
f (x)dx for convergente, então
1
Z
ii. Se
∞
f (x)dx for divergente, então
1
∞
X
an é convergente.
n=1
∞
X
an é divergente.
n=1
1
Exemplos: A p-série
∞
X
1
é convergente se p > 1 e divergente se p ≤ 1.
np
n=1
Critério da Comparação: Suponha que
i. Se
ii. Se
P∞
n=1 an
P∞
e
n=1 bn
sejam séries com termos positivos.
P∞
P∞
n=1 bn for convergente e an ≤ bn para todo n, então
n=1 an também será convergente.
P∞
P∞
n=1 bn for divergente e an ≥ bn para todo n, então
n=1 an será divergente.
Uma série alternada é aquela cujos termos são alternadamente positivos e negativos.
Exemplo:
∞
X
(−1)n−1
n=1
n
=1−
1 1 1 1
+ − + ···
2 3 4 5
Critério da Série Alternada: Se a série alternada
∞
X
(−1)n−1 bn = b1 − b2 + b3 − b4 + b5 − b6 + · · ·
(bn > 0)
n=1
satisfizer
i. bn+1 ≤ bn para todo n
ii. limn→∞ bn = 0
então a série é convergente.
P∞
P
Uma série ∞
n=1 |an | for
n=1 an é chamada absolutamente convergente se a série de valores absolutos
convergente.
P
Uma série ∞
n=1 an é chamada condicionalmente convergente se ela for convergente, mas não for absolutamente convergente.
Teorema: Se uma série
P∞
n=1 an
for absolutamente convergente, então ela é convergente.
O Critério da Razão:
an+1 = L < 1, então a série P∞ an é absolutamente convergente.
i. Se limn→∞ n=1
an an+1 P
> 1, então a série ∞ an é divergente.
ii. Se limn→∞ n=1
an
an+1 = 1, o Critério da Razão não é conclusivo.
iii. Se limn→∞ an O Critéria da Raiz:
p
P
i. Se limn→∞ n |an | = L < 1, então a série ∞
n=1 an é absolutamente convergente.
p
P∞
n
ii. Se limn→∞ |an | = L > 1, então a série n=1 an é divergente.
p
iii. Se limn→∞ n |an | = 1, o Critério da Raiz não é conclusivo.
2