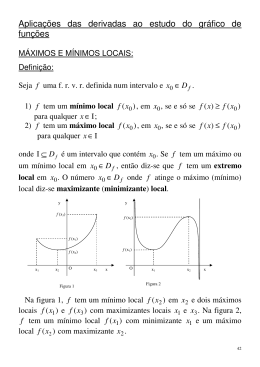
1. Revisão Matemática
Sequências de Escalares
• Uma sequência {xk } diz-se uma sequência de Cauchy se para qualquer ε >0 ∃ algum K
(dependente de ε ) tal que :
x k − xm < ε
para todo
k≥K e
m≥K
• Uma sequência {xk } diz-se ser limitada superiormente (inferiormente) se ∃ algum
escalar b tal que :
x k ≤ b (x k ≥ b ) para ∀k
Diz-se limitada se é limitada superiormente e inferiormente .
Prof. João Sentieiro – ISR
1 º Semestre 2003 / 04
1. Revisão Matemática
Sequências de Escalares
• Uma
sequência
{xk }
diz-se
xk +1 ≤ xk (xk +1 ≥ xk ) , ∀k
xk ↓ x
ser
(x
não-crescente
k
(não-decrescente)
se
↑ x)
PROPOSIÇÃO 17.1:
Qualquer sequência não-crescente ou não-decrescente de escalares converge para um
número possivelmente infinito. Se a sequência é tambem limitada então converge
para um número real finito.
Prof. João Sentieiro – ISR
1 º Semestre 2003 / 04
1. Revisão Matemática
Sequências de Escalares
• O supremo de um conjunto (de escalares) não vazio A , denominado de supA, é
definido como o menor escalar x tal que x ≥ y para ∀y∈ A
NOTA: Se um tal escalar não existir, diz-se que o supremo de A é ∞ .
• O ínfimo é definido de modo semelhante como o maior escalar x tal que x ≤ y para
∀y∈ A
NOTA: Se um tal escalar não existir, diz-se que o ínfimo de A é − ∞ .
Prof. João Sentieiro – ISR
1 º Semestre 2003 / 04
1. Revisão Matemática
Sequências de Escalares
• Dada uma sequência {xk } , o supremo da sequência designado por
supk xk é
definido por sup xk k = 1,2 ,... . (O ínfimo da sequência é definido de modo


semelhante).
• Dada uma sequência {xk } seja:
y m = sup{ x k k ≥ m } e z m = inf{ x k k ≥ m }
A sequências {ym } e {zm} são, respectivamente, não-crescentes e não-decrescentes, e
portanto têm limite (possivelmente infinito) (Proposição 17.1)
O limite de y m é designado por lim sup x m e o limite de zm por lim inf x m .
m→∞
Prof. João Sentieiro – ISR
m →∞
1 º Semestre 2003 / 04
1. Revisão Matemática
Sequências de Escalares
PROPOSIÇÃO 18.1: Seja {xk } uma sequência de escalares.
(a) Verifica-se
inf x k ≤ lim inf x k ≤ lim sup x k ≤ sup x k
k →∞
k
k →∞
k
(b) {x k } converge sse lim inf x k = lim sup x k e, nesse caso, aquelas quantidade s são
k →∞
ambas iguais ao limite de {x k }.
(c) Se x ≤ y
k
k
k →∞
lim inf x k ≤ lim inf y k
k →∞
k →∞
lim sup x k ≤ lim sup y k
Prof. João Sentieiro – ISR
k →∞
k →∞
1 º Semestre 2003 / 04
1. Revisão Matemática
Sequências de Vectores
• Uma sequência {xk } de vectores em ℜ n diz-se convergir para x ∈ℜ n se a coordenada i de xk
convergir para coordenada i de x para qualquer i .
xk → x
ou lim x k = x
k →∞
• {xk } diz-se limitada (ou uma sequência de Cauchy) se cada uma das correspondentes
sequências de coordenadas for limitada (ou uma sequência de Cauchy respectivamente).
DEFINIÇÃO 5.1:
Diz-se que um vector x ∈ℜ n é um ponto limite de uma sequência {xk } em ℜ n se existe uma
subsequência de {xk } que converge para x. Seja A um subconjunto de ℜ n .
Diz-se que x ∈ℜ n é um ponto limite de A se existe uma sequência {xk } consistindo de elementos
de A, que converge para x.
Prof. João Sentieiro – ISR
1 º Semestre 2003 / 04
1. Revisão Matemática
Sequências de Vectores
PROPOSIÇÃO 19.1:
(a) Uma sequência limitada de vectores em ℜ n converge sse tem um único
ponto limite.
(b) Uma sequência em ℜ n converge sse é uma sequência de Cauchy.
(c) Qualquer sequência limitada em ℜ n tem pelo menos um ponto limite.
(d) Seja {xk } uma sequência de escalares. Se lim sup x k ( lim inf x k ) é finito então
k →∞
k →∞
é o maior (menor) ponto limite de {xk }.
NOTA: Se p é um inteiro positivo e h : ℜn → ℜm , então diz-se que h(x ) = 0  x

sse lim
h(x k )
xk → 0 xk
p
=0
para todas as sequências {xk } , com xk ≠ 0 para todo o k, que
convergem para 0 .
Prof. João Sentieiro – ISR
p


1 º Semestre 2003 / 04
1. Revisão Matemática
Conjuntos Fechados e Abertos
DEFINIÇÃO 6.1:
(a) Um conjunto A ⊂ ℜ n diz-se fechado se contem todos os seus pontos limite.
Diz-se aberto se o seu complemento (o conjunto x x ∉A ) é fechado.


(b) Diz-se limitado se ∃ algum c ∈ℜ n tal que a amplitude de qualquer coordenada
de qualquer elemento de A é menor do que c .
(c) Diz-se compacto se qualquer sequência de elementos de A tem uma
subsequência que converge para um elemento de A.
(d) A vizinhança de um vector x é um conjunto aberto contendo x.
(e) Se A ⊂ ℜ n e, diz-se que x é um ponto interior de A se existe uma vizinhança
de x que está contida em A.
(f) Um vector x ∈ A que não é um ponto interior de A diz-se ser um ponto de
fronteira de A.
Prof. João Sentieiro – ISR
1 º Semestre 2003 / 04
1. Revisão Matemática
Conjuntos Fechados e Abertos
PROPOSIÇÃO 20.1:
(a) A união de um número finito de conjuntos fechados é fechada.
(b) A intersecção de conjuntos fechados é fechada.
(c) A união de conjuntos abertos é aberta.
(d) A intersecção de um número finito de conjuntos abertos é aberta.
(e) Um conjunto é aberto sse todos os seus elementos são pontos interiores.
(f) Qualquer subespaço de ℜ n é fechado
(g) Um subconjunto de ℜ n é compacto sse é fechado e limitado
Prof. João Sentieiro – ISR
1 º Semestre 2003 / 04
1. Revisão Matemática
Continuidade
Seja A ⊂ ℜ n e f : A → ℜn . Seja x um ponto limite de A.
- Se a sequência



f  x k  tem um limite comum z para qualquer sequência {xk } de

elementos de A tal que lim x k = x , então podemos escrever que :
k →∞
lim f (y ) = z
y →x
A notação lim y ↑ x f (y ) significa limite de f  x k  onde {xk } é uma subsequência de
elementos de A convergindo para x e satisfazendo xk ≤ x .
Prof. João Sentieiro – ISR
1 º Semestre 2003 / 04
1. Revisão Matemática
Continuidade
DEFINIÇÃO 7.1: Seja A ⊂ ℜ m
(a) Uma função f : A → ℜn diz-se continua num ponto x ∈ A se
lim f (y ) = f (x ).
y →x
Diz-se continua em A se é continua em qualquer x ∈ A .
(b) Uma função real f : A → ℜ diz-se semi-contínua superior num vector x ∈ A se
f (x ) ≥ lim sup f ( x k
)
k →∞
para qualquer sequência {xk } de elementos de A convergindo para x .
Prof. João Sentieiro – ISR
1 º Semestre 2003 / 04
1. Revisão Matemática
Continuidade
(c) Uma função real f : A → ℜ diz-se coerciva se lim f (x k ) = ∞ para qualquer
k → ∞
sequência {xk } de elementos de A tal que xk → ∞ para alguma norma • .
(d) Seja A ⊂ ℜ . Uma função f : A → ℜn diz-se contínua à direita, num ponto x ∈ A se
lim y ↓x f (y ) = f (x )
NOTA : É fácil de ver que quando A ⊂ ℜ , uma função não-decrescente e contínua à
direita f : A → ℜ é semi-contínua superior.
Prof. João Sentieiro – ISR
1 º Semestre 2003 / 04
1. Revisão Matemática
Continuidade
PROPOSIÇÃO 21.1:
(a) A composição de duas funções contínuas é contínua.
(b) Qualquer norma do vector ℜ n é uma função contínua .
(c) Seja f : ℜm → ℜn contínua, e seja A ⊂ ℜn aberto (fechado).
Então o conjunto x ∈ℜm f (x )∈ A é aberto (fechado).
Prof. João Sentieiro – ISR
1 º Semestre 2003 / 04
1. Revisão Matemática
Conjuntos Fechados e Abertos
PROPOSIÇÃO 22.1: (Teorema de Weierstrass)
Seja A um subconjunto não vazio de ℜ n e seja f : A → ℜ uma função semi-contínua
inferior em todos os pontos de A.
Assuma que uma das seguintes condições se verifica :
(1) A é compacto
(2) A é fechado e f é coerciva
(3) Existe um escalar γ tal que o conjunto x ∈ A f (x ) ≤ γ  é não vazio e compacto.
Então, existe um vector x∈ A tal que
f ( x ) = inf f ( z)
z∈A
Prof. João Sentieiro – ISR
x = arg min f ( z)
z∈A
1 º Semestre 2003 / 04
1. Revisão Matemática
Conjuntos Fechados e Abertos
PROPOSIÇÃO 23.1: (Propriedade de equivalência de normas):
Para quaisquer duas normas • e • ′ em ℜ n , existe alguma constante positiva c ∈ℜ
tal que x ≤ c x ′ ∀x ∈ ℜ n
NOTA : Se uma sequência converge com respeito a uma norma, então converge com
respeito a todas as outras normas
PROPOSIÇÃO 24.1:
Se um subconjunto de ℜ n é aberto (fechado, limitado, ou compacto) para alguma
norma, então é aberto (fechado, limitado, ou compacto) para todas as outras normas.
Prof. João Sentieiro – ISR
1 º Semestre 2003 / 04
2. Análise Convexa
Conjuntos e Funções Convexas
DEFINIÇÃO 1.2: Seja C um subconjunto de ℜ n . Diz-se que C é convexo se
α x + (1 − α )y ∈ C ∀x , y ∈ C , ∀α ∈ [0 ,1]
(D1.2)
DEFINIÇÃO 2.2: Seja C um subconjunto convexo de ℜ n . A função f : C → ℜ diz-se
convexa se
f (αx + (1 − α )y ) ≤ α f (x ) + (1 − α ) f (y )
OBS:
∀x , y ∈ C ,
∀α ∈ [0 ,1]
(D2.2)
(a) f diz-se côncava se –f é convexa
(b) f diz-se estrictamente convexa se a desigualdade em (D2.2) for estricta para
todos os x , y ∈C com x ≠ y e ∀ α ∈  0,1 .
Prof. João Sentieiro – ISR
1 º Semestre 2003 / 04
2. Análise Convexa
Conjuntos e Funções Convexas
PROPOSIÇÃO 1.2:
(a) Para qualquer colecção
Ci i ∈I  de conjuntos convexos, o conjunto de



intersecção ∩i ∈ I Ci é convexo.
(b) A soma vectorial  x1 + x2 x1 ∈C1 , x2 ∈C2  de dois conjuntos convexos C1 e C2 é
convexo.
(c) A imagem de um conjunto sob uma transformação linear é convexa.
(d) Se C é um conjunto convexo e f : C → ℜ é uma função convexa, os conjuntos
{ x ∈C
f (x) ≤ α } e { x ∈C f (x) < α } são convexos para todos os escalares α .
Prof. João Sentieiro – ISR
1 º Semestre 2003 / 04
2. Análise Convexa
Conjuntos e Funções Convexas
PROPOSIÇÃO 2.2:
(a) Uma funçaõ linear é convexa.
(b) Qualquer norma de um vector é convexa.
(c) A soma pesada de funções convexas, (com pesos positivos), é convexa.
(d) Se I é um conjunto de índices, C ⊂ ℜn é um conjunto, e f i : C → ℜn é convexo
para cada i ∈ I , então a função h :C → (− ∞,+∞] definida por :
h(x ) = sup f i (x ) é também convexa.
i∈I
Prof. João Sentieiro – ISR
1 º Semestre 2003 / 04
2. Análise Convexa
Caracterização de Funções Convexas Diferenciáveis
PROPOSIÇÃO 3.2:
Seja C ⊂ ℜn um conjunto convexo e seja f : ℜn → ℜ diferenciável em C.
(a) A função f é convexa em sse.
f ( z) ≥ f ( x ) + ( z − x )′∇f ( x )
∀x , z ∈ C .
(b) Se a desigualdade anterior for estrita sempre que x ≠ z , então f é estritamente
convexa em C.
Prof. João Sentieiro – ISR
1 º Semestre 2003 / 04
2. Análise Convexa
Caracterização de Funções Convexas Diferenciáveis
PROPOSIÇÃO 4.2:
Seja C ⊂ ℜn um conjunto convexo e seja
f : ℜn → ℜ dupla e continuamente
diferenciável em C, e seja Q uma matriz real simétrica n× n .
(a) Se ∇2 f (x ) é positiva semidefinida para todo x∈C , então f é convexa em C .
(b) Se ∇2 f (x ) é positiva definida para qualquer x∈C , então f é estritamente
convexa em C .
(c) Se C = ℜn e f é convexa, então ∇2 f (x ) é positiva semidefinida para todo x∈C .
(d) A função quadrática f (x) = x′Qx , onde Q é uma matriz simétrica. É convexa
sse Q é positiva semidefinida. Para além disso, f é estritamente convexa sse Q
é positiva definida.
OBS: (c) também se verifica quando se assume que C tem um interior não vazio (em
vez de ser igual a ℜ n ).
Prof. João Sentieiro – ISR
1 º Semestre 2003 / 04