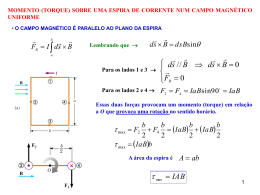
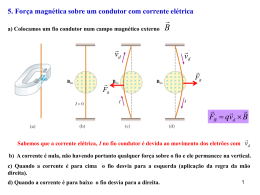
Campo –magnético
Magnetostática
Lei de Biot Savart
• Um imã produz um campo magnético em
todos os pontos do espaço ao seu redor.
Imã permanente e suas linhas de
Campo magnético
Pólos magnéticos iguais se repelem
Campo magnético - eletroimã
Campo magnético – Regra da
mão direita
A força Magnética
• A força magnética
que atua sobre uma
partícula é
diretamente
proporcional à carga
e à velocidade da
partícula.
A força Magnética em um fio
percorrido por uma corrente
• O campo
magnético
exerce uma
força lateral
sobre os elétrons
em movimento.
Torque sobre uma espira percorrida por
uma corrente
• As forças magnéticas produzem
um torque sobre a espira, que
tende a girar.
Torque sobre uma espira percorrida por
uma corrente
F  iaB
b
b

 

   iaB sen    iaB sen   iabBsen 
2
2

 

O Dipolo Magnético

an
• Definindo o momento de
dipolo magnético:


  iAan
• Torque exercido pelo campo
sobre o dipolo magnético:
  
T  B
A lei de Biot e Savart
• A lei de Biot e Savart
relaciona o campo
magnético com a
corrente que o
produz.


  o ids  r
dB 
2
4 r
• Constante de
permeabilidade
o  4 10 T  m / A
7
A lei de Biot e Savart
• A lei de Biot e Savart
será aplicada em
problemas de
magnetostática:
correntes em regime
produzindo campos
constantes.
• A lei de Biot e Savart é uma lei experimental e
pode ser considerada uma variação algébrica da
lei de Ampère.
A lei de Biot e Savart
 
 o idl  r
dB 
2
4 r


B  o H
 

1 idl  r
dH 
2
4 r
Indução magnética a uma distância de um
fio retilíneo
 
 o idl  r
dB 
2
4 r
sen  sen(   )
  o idl
dB 
sen 
2
4 r
 o idl
R
dB 
2
2
2 1/ 2
4 r (l  R )
Indução magnética a uma distância de um
fio retilíneo
 oi
Rdl
dB 
2
2 3/ 2
4 (l  R )
 oi 
R
B
dl
2
2 3/ 2

2 0 (l  R )

 oi 

l
 2

B
2 1/ 2 
2R  (l  R )  0
 oi
B
2R
Exercício: Calcule a indução magnética devido à corrente i, no ponto
C?