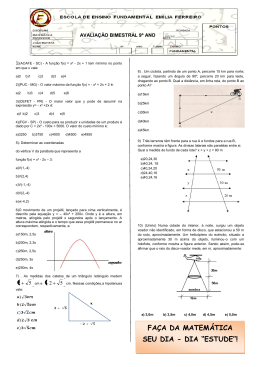
LANÇAMENTO OBLÍQUO
(PROF. VADO)
A altura máxima h alcançada pela bola e o
deslocamento horizontal x do carrinho, valem,
respectivamente:
01) PUCSP- Suponha que em uma partida de
futebol, o goleiro, ao bater o tiro de meta, chuta a
bola, imprimindo-lhe
lhe uma velocidade V0 cujo
vetor forma, com a horizontal, um ângulo α.
Desprezando a resistência do ar, são feitas as
afirmações abaixo.
a) h = 16,2 m; x = 18,0 m
b) h = 16,2 m; x = 9,0 m
c) h = 8,1 m; x = 9,0 m
d) h = 10,0 m; x = 18,0 m
I - No ponto mais alto da trajetória, a velocidade
vetorial da bola é nula.
II - A velocidade inicial V0 pode ser decomposta
dec
segundo as direções horizontal e vertical.
III - No ponto mais alto da trajetória é nulo o valor
da aceleração da gravidade.
IV - No ponto mais alto da trajetória é nulo o valor
VY da componente vertical da velocidade.
Estão corretas:
a) I, II e III
b) I, III e IV
c) II e IV
d) III e IV
e) I e II
02) UECE- Uma bola é lançada verticalmente para
cima, com velocidade de 18 m/s, por um rapaz
situado em carrinho que avança segundo uma reta
horizontal, a 5,0 m/s. Depois de atravessar um
pequeno túnel, o rapaz volta a recolher a bola, a
qual acaba de descrever umaa parábola, conforme a
figura. Despreza-see a resistência do ar e g=10m/s2.
03) UTFPR- Um canhão lança projéteis com
velocidade 50 m/s segundo um ângulo α com a
horizontal, tal que senα
α =0,8 e cosα =0,6.
Desprezando a altura do canhão e a resistência do
ar e supondo 10 m/s2 a aceleração da gravidade
local, assinale a alternativa correta.
a)) Os projéteis atingem a altura máxima 8 s após
terem sido lançados.
b)) A altura máxima atingida pelos projéteis é igual
a 160 m.
c)) Os projéteis atingem o solo a uma distância
igual a 120 m do ponto de lançamento.
d) O raio de curvatura da trajetória parabólica
no ponto de altura máxima é 90 m.
e)) A componente horizontal da velocidade dos
projéteis ao atingirem o solo é 40 m/s.
04) UEL- Um projétil é atirado com velocidade de
40m/s, fazendo ângulo de 37° com a horizontal. A
64m do ponto de disparo, há um obstáculo de
altura 20m. Adotando g=10m/s2, cos37°=0,80 e
sen37°=0,60, pode-se
se concluir que o projétil
a) passa à distância de 2,0 m acima do obstáculo.
b) passa à distância de 8,0 m acima do
d obstáculo.
c) choca-se
se com o obstáculo a 12 m de altura.
d) choca-se
se com o obstáculo a 18 m de altura.
e) cai no solo antes de chegar até o obstáculo.
05) UEM- Uma pedra é lançada com um ângulo
de 450 em relação
lação ao eixo horizontal x e na direção
positiva de x. Desprezando-se
se a resistência do ar,
quais dos gráficos melhor representam a
componente horizontal da velocidade (vx) versus
tempo (t) e a componente vertical da velocidade
(vy) versus tempo (t), respectivamente?
a)
b)
c)
d)
e)
vx versus t
I
II
II
II
IV
e
e
e
e
e
vy versus t
IV
I
III
V
V
06) FEI- Um bombeiro deseja apagar um incêndio
em um edifício. O fogo está a 10m do chão. A
velocidade da água é v=30m/s e o bombeiro segura
a mangueira com um ângulo de 30° em relação ao
solo. Obs. desprezar a altura da mangueira ao solo.
a) Qual é a distância máxima entre o bombeiro e o
edifício?
b) Qual é a altura máxima que a água atinge nestas
condições?
Gabarito: a) 30 3 m ; b) 11,25m.
07) UFPI- Dois projéteis são lançados de uma
mesma posição, com velocidades iniciais de
mesmo módulo v0 e diferentes ângulos de
lançamento. As trajetórias dos projéteis estão
mostradas na figura a seguir. Sobre os módulos das
velocidades e das acelerações dos projéteis nos
pontos 1 e 2 podemos afirmar corretamente que:
a) v1 > v2 e a1 = a2.
b) v1 = v2 e a1 = a2.
c) v1 < v2 e a1 = a2.
d) v1 = v2 e a1 > a2.
e) v1 < v2 e a1 > a2.
08) UFMG- Clarissa chuta, em seqüência, três
bolas - P, Q e R -,, cujas trajetórias estão
representadas nesta figura:
Sejam tP, tQ e tR os tempos gastos,
respectivamente, pelas bolas P, Q e R, desde o
momento do chute até o instante em que atingem o
solo.
Considerando-se
se essas informações, é CORRETO
afirmar que
a) tQ > tP = tR
b) tR > tQ = tP
c) tQ > tR > tP
d) tR > tQ > tP
09) UFMG- Uma caminhonete move-se,
move
com
aceleração constante, ao longo de uma estrada
plana e reta, como representado na figura:
A seta indica o sentido da velocidade e o da
aceleração dessa caminhonete.
Ao passar pelo ponto P, indicado na figura, um
passageiro, na carroceria
oceria do veículo, lança uma
bola para cima, verticalmente em relação a ele.
Despreze a resistência do ar.
Considere que, nas alternativas a seguir, a
caminhonete está representada em dois instantes
consecutivos.
Assinale a alternativa em que está MAIS BEM
representada a trajetória da bola vista por uma
pessoa, parada, no acostamento da estrada.
Gabarito: b
10) PUCRS- Uma esfera de aço é lançada
obliquamente com pequena velocidade, formando
um ângulo de 45 graus com o eixo horizontal.
Durante sua trajetória, desprezando--se o atrito com
o ar, pode-se afirmar que
a) a velocidade é zero no ponto de altura máxima.
b) a componente
ponente vertical da velocidade mantém-se
mantém
constante em todos os pontos.
c) a componente horizontal da velocidade é
variável em todos os pontos.
d) o vetor velocidade é o mesmo nos pontos de
lançamento e de chegada.
e) a componente vertical da velocidade é nula no
ponto de máxima altura.
11) UTFPR- Um garoto deseja derrubar uma
manga que se encontra presa na mangueira
atirando uma pedra. A distância horizontal do
ponto em que a pedra sai da mão do garoto até a
manga é de 10 m, enquanto a vertical é 5 m. A
pedra sai da mão do garoto, fazendo um ângulo de
45º com a horizontal. Qual deve ser o módulo da
velocidade inicial da pedra, em m/s, para que o
garoto acerte a manga?
(Considere: g = 10 m/s2; sen 45º = cos 45º = 2 /2)
a) 5 2
b) 10 2
c) 15
d) 20 2
e) 25
12) PUCCAMP- Observando a parábola do dardo
arremessado por um atleta, um matemático
resolveu obter uma expressão que lhe permitisse
calcular a altura y, em metros, do dardo em relação
ao solo, decorridos t segundos do instante de seu
lançamento (t = 0). Se o dardo chegou
ch
à altura
máxima de 20 m e atingiu o solo 4 segundos após
o seu lançamento, então, desprezada a altura do
atleta, a expressão que o matemático encontrou foi
a) y = - 5t2 + 20t
b) y = - 5t2 + 10t
c) y = - 5t2 + t
d) y = -10t2 + 50
e) y = -10t2 + 10
13) MACKENZIE- Um corpo é lançado
horizontalmente do alto de uma torre e atinge o
solo horizontal com velocidade de 37,5m/s
formando 53° com a horizontal. A altura da torre é
de:
Obs.: Despreze as resistências ao movimento.
Dados: g=10m/s2, cos 53°=0,6 e sen 53°=0,8.
a) 20 m
b) 30 m
c) 40 m
d) 45 m
e) 50 m
14) PUCCAMP- Um projétil é lançado segundo
um ângulo de 30° com a horizontal, com uma
velocidade de 200m/s. Supondo a aceleração da
gravidade igual e 10m/s2 e desprezando a
resistência do ar, o intervalo de tempo entre as
passagens do projétil pelos pontos de altura 480 m
acima do ponto de lançamento, em segundos, é
DADOS:
sen 30° = 0,50
cos 30° = 0,87
a) 2,0
b) 4,0
c) 6,0
d) 8.0
e) 12
15) UFPR- Um jogo consiste em lançar uma
bolinha com um dispositivo dotado de mola, cujo
objetivo é atingir um ponto predefinido na parede,
conforme ilustrado na figura. O ponto A representa
a posição da bolinha no momento imediatamente
seguinte ao seu lançamento. Considere g = 10
m/s2. Com base nesses dados, a velocidade de
lançamento da bolinha deve ser:
B
0,4 m
A
45°
0,5 m
a) 5,0 m/s.
b) 4,0 m/s.
c) 10 m/s.
d) 20 m/s.
e) 3,0 m/s.
16) UNICAMP- Até os experimentos de Galileu
Galilei, pensava-se que quando um projétil era
arremessado, o seu movimento devia-se ao
impetus, o qual mantinha o projétil em linha reta e
com velocidade constante. Quando o impetus
acabasse, o projétil cairia verticalmente até atingir
o chão. Galileu demonstrou que a noção de
impetus era equivocada. Consideremos que um
canhão dispara projéteis com uma velocidade
inicial de 100m/s, fazendo um ângulo de 30° com
a horizontal. Dois artilheiros calcularam a
trajetória de um projétil: um deles, Simplício,
utilizou a noção de impetus, o outro, Salviati, as
idéias de Galileu. Os dois artilheiros concordavam
apenas em uma coisa: o alcance do projétil.
Considere 3 = 1,8. Despreze o atrito com o ar.
a) Qual o alcance do projétil?
b) Qual a altura máxima alcançada pelo projétil,
segundo os cálculos de Salviati?
c) Qual a altura máxima calculada por Simplício?
Gabarito: a) ≅ 900 m.; b) ≅ 125 m ; c) ≅ 540 m.