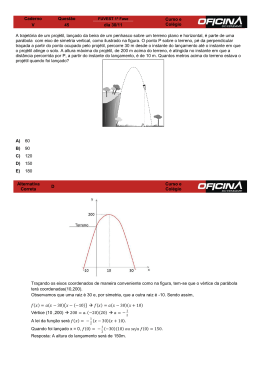
AVALIAÇÃO BIMESTRAL 9º ANO
1)(ACAFE - SC) - A função f(x) = x² - 2x + 1 tem mínimo no ponto
em que x vale:
2)(PUC - MG) - O valor máximo da função f(x) = - x² + 2x + 2 é:
8) . Um ciclista, partindo de um ponto A, percorre 15 km para norte;
a seguir, fazendo um ângulo de 90º, percorre 20 km para leste,
chegando ao ponto B. Qual a distância, em linha reta, do ponto B ao
ponto A?
a)2
a)15km
a)0
b)1
c)2
b)3
c)4
d)3
e)4
d)5
e)6
3)(CEFET - PR) - O maior valor que y pode de assumir na
expressão y= - x² +2x é:
a)1 b)2
c)3
d)4
b)25km
c)35km
e)5
4)(FGV - SP) - O custo para se produzir x unidades de um produto é
dado por C = 2x² - 100x + 5000. O valor do custo mínimo é:
d)40km
e)45km
a)3250
b)3750
c)4000
d)4500
e)4950
5)- Determinar as coordenadas
do vértice V da parábola que representa a
função f(x) = x² - 2x – 3:
9) Três terrenos têm frente para a rua A e fundos para a rua B,
conforme mostra a figura. As divisas laterais são paralelas entre si.
Qual a medida de fundo de cada lote? x + y + z = 80 m
a)20,24,30
b)40,24, 18
c)40,24,20
d)24,40,16
e)40,24,16
a)V(1,-4)
b)V(2,4)
c)V(-1,-4)
d)V(2,-4)
e)v(-4,2)
6)O movimento de um projétil, lançado para cima verticalmente, é
descrito pela equação y = – 40x² + 200x. Onde y é a altura, em
metros, atingida pelo projétil x segundos após o lançamento. A
altura máxima atingida e o tempo que esse projétil permanece no ar
correspondem, respectivamente, a:
a)150m, 2,5s
b)200m, 2,3s
c)250m, 2,5s
10) (Unirio) Numa cidade do interior, à noite, surgiu um objeto
voador não identificado, em forma de disco, que estacionou a 50 m
do solo, aproximadamente. Um helicóptero do exército, situado a
aproximadamente 30 m acima do objeto, iluminou-o com um
holofote, conforme mostra a figura anterior. Sendo assim, pode-se
afirmar que o raio do disco-voador mede, em m, aproximadamente:
d)250m, 3s
e)250m, 4s
7) . As medidas dos catetos de um triângulo retângulo medem
2
5
cm e
2
5
cm. Nessas condições,a hipotenusa
vale:
a) 3,0m
b) 3,5m
c) 4,0m
d) 4,5m
e) 5,0m
FAÇA DA MATEMÁTICA
SEU DIA - DIA “ESTUDE”!