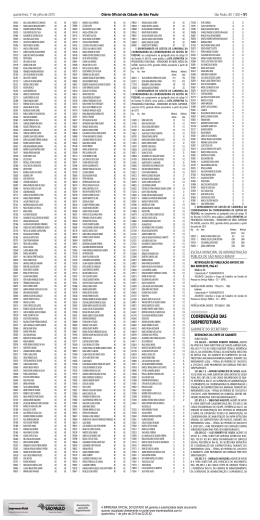
Universidade Federal de Alagoas
Centro de Tecnologia
Estatística
Aula 22
Prof. Marllus Gustavo Ferreira Passos das Neves
Aula 22

Teste de Hipóteses para duas variâncias
Inferência sobre 2 variâncias
Suposições:
1) As 2 populações são independentes uma da outra;
2) As 2 populações são, cada uma delas, normalmente
distribuídas
s  maior das 2 variâncias amostrais
2
1
n1  tamanho da amostra com a maior variância
 12 variância da população da qual a amostra com a
maior variância foi extraída
Os símbolos n2, s22 e
amostra e população
 22 são usados para a outra
Inferência sobre 2 variâncias
Estatística de teste F  s
2
1
2
2
s
~ distribuição F
Graus de liberdade do numerador gl1 = n1 – 1
Graus de liberdade do denominador gl2 = n2 – 1
Sejam W e Y variáveis aleatórias independentes
qui-quadrado, com gl1 e gl2 graus de liberdade,
respectivamente. Então a razão
F = (W/gl1) / (Y/gl2)
Segue a distribuição F com gl1 graus de liberdade
do numerador e gl2 graus de liberdade do
denominador
Inferência sobre 2 variâncias
Propriedades da distribuição F
1) Ela não é simétrica
2) Os valores de F não podem ser negativos
3) A forma exata da distribuição F depende de 2 diferentes
graus de liberdade
Inferência sobre 2 variâncias
Interpretação da estatística de teste F: se as 2
populações têm, realmente, variâncias iguais, então a
razão s12/s22 tende a se aproximar de 1, porque os
valores de s12 e s22 tendem a se aproximar um do
outro. Mas se as 2 populações têm variâncias
radicalmente diferentes, s12 e s22 tendem a ser nos
muito diferentes. Representando a maior das
variâncias amostrais por s12 vemos que a razão
s12/s22 será um no grande sempre que s12 e s22
tiverem valores muito distantes um do outro.
Consequentemente, um valor de F próximo de 1 será
evidência em favor de 12=22, mas um grande valor
de F será evidência contra a igualdade acima
Aplicações
A tabela abaixo resume estatísticas referentes à amostras
de coca-cola e Pepsi. Use um nível de significância de 0,05
para testar a afirmativa de que os pesos de Coca normal e os
pesos de Pepsi normal têm o mesmo desvio padrão
n
Média amostral
s
Coca normal
Pepsi normal
36
36
0,81682
0,82410
0,007507
0,005701
1) Parâmetro de interesse  12 - 12
2) Hipótese nula H0  12 - 12 = 0
3) Hipótese alternativa H1  12 - 12 ≠ 0
4) Nível de significância  a = 0,05
5) Estatística de teste  F
6) Região de rejeição para a estatística
Aplicações
Estatística de teste
s12 0,0075072
F 2 
 1,7339
2
s2 0,005701
7) Grandezas amostrais necessárias
s12 = 0,0075072 e s22 = 0,0057012
Aplicações
8) Decisão Valor crítico de F = 1,8752
gl1 = gl2 = 36 – 1 = 35
olhando em 0,025
na cauda direita
Como F de teste cai na região de
não rejeição, não há evidência
estatística suficiente, ao nível de
significância de 5%, para afirmar
que as 2 variâncias sejam iguais
Resumo dos testes
n1
n2
X ~ N(m,2)
X1
X2
s
s
...
z1
z2
2
1
2
2
k amostras
nk
Xk
s
2
k
zk
t1
12
t2
 22
tk
 k2
F1
F2
Fk
2
2
s
Xi  μ
Xi  μ
(n

1)

s
2
i1
i
i
z

t



F

2
onde: i / n , i s / n , i
e i s2

i
i
i
i2
Universidade Federal de Alagoas
Centro de Tecnologia
Estatística
Aula 22
Prof. Marllus Gustavo Ferreira Passos das Neves