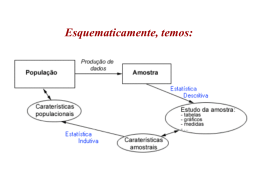
1
EXERCÍCIOS DE REVISÃO – ESTATÍSTICA ELEMENTAR
3o PERÍODO - ADMINISTRAÇÃO
ASSUNTOS : População, amostragem, distribuição de freqüência,
Medidas de posição e Medidas de dispersão, Probabilidade.
1) Uma população de trabalhadores de um garimpo é constituída de crianças,
adolescentes e adultos, de acordo com a tabela abaixo.
GÊNEROS
MASCULINO
FEMININO
TOTAIS►
FAIXAS ETÁRIAS
6 a 12 anos 13 a 20 anos
56
124
16
71
72
195
21 a 55 anos
64
34
98
TOTAIS
244
121
365
1o) Sorteando-se um desses trabalhadores, qual é a probabilidade de sair
a) um homem?
b) uma mulher com menos de 21 anos?
c) um homem com até 12 anos?
d) uma mulher com pelo menos 21 anos?
e) um trabalhador(a) com idade entre 7 e 21 anos?
2o) Responda :
a) Qual é o percentual de cada gênero de trabalhadores ?
b) Qual é o percentual de cada faixa etária de trabalhadores?
c) Qual é o percentual de cada faixa etária feminina?
d) Qual é o percentual de cada faixa etária masculina?
3o) Considere que uma amostragem proporcional selecionará uma amostra de 28
trabalhadores para verificar a incidência de DST. Determine quantos indivíduos
comporão cada estrato, se os estratos são
a) os gêneros.
b) as faixas etárias.
4o) Considere que uma amostragem proporcional, considerando os gêneros como
estratos, selecionou 17 homens.
a) Qual é o total da amostra?
b) Quantas mulheres foram selecionadas?
5o) Considere que uma amostragem proporcional, considerando as faixas etárias como
estratos, selecionou 17 indivíduos de 13 a 20 anos.
a) Qual é o total da amostra?
b) Quantos indivíduos de cada faixa foram selecionados?
2
6o) Considere que uma amostragem proporcional, considerando as faixas etárias como
estratos, selecionou 15 indivíduos de 13 a 55 anos.
a) Qual é o total da amostra?
b) Quantos indivíduos de cada faixa foram selecionados?
2)
POPULAÇÃO DISCENTE DE UMA INSTIUIÇÃO DE ENSINO SUPERIOR
CURSOS
GÊNERO
ADMINISTRAÇÃO
FILOSOFIA
DIREITO
Masculino
220
240
580
Feminino
200
230
560
FONTE : Secretaria Acadêmica da instituição
1o) Sorteando-se um desses estudantes, qual é a probabilidade de sair
a) um homem?
b) uma mulher que estuda DIREITO?
c) um homem que estuda ADMINISTRAÇÃO?
d) uma mulher que estuda ADMINISTRAÇÃO ou DIREITO?
e) um(a) estudante de FILOSOFIA ou DIREITO?
2o) Responda :
a) Qual é o percentual de cada gênero de estudantes ?
b) Qual é o percentual de estudantes de cada curso?
c) Qual é o percentual de cada faixa etária feminina?
d) Qual é o percentual de cada faixa etária masculina?
3o) Considere que uma amostragem proporcional selecionará uma amostra de 36
estudantes para verificar a procedência acadêmica. Determine quantos indivíduos
comporão cada estrato, se os estratos são
a) os gêneros.
b) os cursos.
4o) Considere que uma amostragem proporcional, considerando os gêneros como
estratos, selecionou 22 homens.
a) Qual é o total da amostra?
b) Quantas mulheres foram selecionadas?
5o) Considere que uma amostragem proporcional, considerando os cursos como
estratos, selecionou 27 indivíduos que estudam DIREITO.
a) Qual é o total da amostra?
b) Quantos indivíduos de cada curso foram selecionados?
6o) Considere que uma amostragem proporcional, considerando os cursos como
estratos, selecionou 25 indivíduos de FILOSOFIA ou DIREITO.
3
a) Qual foi o total da amostra?
b) Quantos indivíduos de cada curso foram selecionados?
3) Uma universidade ofereceu, em determinado semestre, vagas para as disciplinas
CÁLCULO (C), HISTÓRIA DAS CIÊNCIAS (HC) e PSICOLOGIA (P) para os
estudantes de certo período, de acordo com a tabela seguinte, em que a segunda
linha mostra os números de estudantes matriculados por disciplina.
C
45
HC
38
P
48
C e HC
18
CeP
15
HC e P
12
C,HCe P
7
NADA
3
1o) Construa diagramas de Venn, mostrando a distribuição das matrículas por
disciplina.
2o) Escolhendo-se aleatoriamente um dos estudantes do período considerado, qual
é a probabilidade de sair um que
a) esteja matriculado apenas em CÁLCULO?
b) esteja matriculado apenas em uma das disciplinas?
c) esteja matriculado em CÁLCULO ou PSICOLOGIA?
d) esteja matriculado em CÁLCULO, HISTÓRIA DAS CIÊNCIAS ou
PSICOLOGIA?
e) esteja matriculado nas três disciplinas?
f) não esteja matriculado?
3o) Um estudo sobre os estudantes do período focado coletará uma amostra de 24
estudantes, considerando as disciplinas como estratos. Calcule o número de
estudantes que comporão cada estrato e os respectivos subestratos.
4o) Sendo as disciplinas os estratos, quantos estudantes matriculados em cada
disciplina comporão a amostra total se foram escolhidos 2 estudantes
matriculados nas três disciplinas?
4) Considerando a distribuição dada no exercício 1, determine
a) a média das idades.
b) a mediana das idades.
c) a moda das idades.
5) Determine a média, a moda e a mediana das variáveis dadas em cada caso a seguir.
a) Alturas , em centímetros , de 12 atletas:
176,177,177,178,178,178,179,180,182,184,190 e 202
b) Número de pessoas do grupo familiar de 13 famílias: 3 , 3 , 4 , 4 , 5 , 5 , 5 , 5 , 5 , 6 ,
6 , 7 e 7;
4
c) Número de filhos de 140 casais:
i
1
2
3
4
5
No FILHOS (x)
2
3
4
5
6
TOTAIS ►
f
32
38
24
27
19
140
fx
fr
Fb
100%
d) Notas de Estatística dos 140 alunos das turmas de mesmo período:
i
1
2
3
4
5
6
7
8
NOTAS(x)
3
4
5
6
7
8
9
10
TOTAIS ►
f
22
26
20
24
18
12
10
8
fx
fr
Fb
100%
e) Tempo,em anos,de contribuição à previdência oficial de 320 trabalhadores:
contribuíram durante 12 anos,
anos,
1
deles
10
2
contribuíram durante 13 anos, 30% deles durante 14
5
3
contribuíram durante 15 anos e 4 trabalhadores contribuíram durante 16 anos;
16
f) Tempo,em anos,de experiência profissional dos19 técnicos de uma empresa de
computadores: 2 , 2 , 3, 4, 5, 5, 5 , 6 , 6 , 7 , 7 , 7 , 7 , 7 , 8 , 9 , 10 , 11 e 12;
5
Emanuel Czuber matemático alemão. Formou –se em uma escola
secundária de Realschule em 1869 e continuou seus estudos na
Universidade Técnica Alemã em Praga. Estudou profundamente a
Teoria das probabilidades e desenvolveu uma fórmula para o cálculo
da Moda das distribuições com classes:
Mo = ℓ +
Em que ℓ é o limite inferior da classe modal, D 1 é a diferença entre a
freqüência da classe modal e a da classe anterior a ela, D 2 é a diferença
entre a freqüência da classe modal e da classe posterior a ela e h é a
amplitude da classe modal.
6) Determine a média, a moda bruta, a moda absoluta (fórmula de Czuber) e a mediana
das variáveis dadas em cada caso a seguir.
a) Salários de uma amostra de 28 dos funcionários de uma empresa:
i
1
2
3
4
5
SALÁRIOS
[650 , 700[
[700 , 750[
[750 , 800[
[800 , 850[
[850 , 900[
TOTAIS ►
f
4
6
7
5
6
28
xM
f xM
fr
Fb
100%
b) Número de jogos profissionais realizados por 210 jogadores de futebol:
i
1
2
3
4
5
6
JOGOS
[125 , 175[
[175 , 225[
[225 , 275[
[275 , 325[
[325 , 375[
[375 , 425[
TOTAIS ►
f
58
42
39
31
27
13
210
xM
fxM
fr
Fb
6
c) Alturas, em centímetros, de uma amostra com 48 atletas de uma olimpíada:
i
1
2
3
4
5
6
7
ALTURAS
[165 , 172[
[172 , 179[
[179 , 166[
[166 , 173[
[173 , 180[
[180 , 187[
[187 , 194[
TOTAIS ►
f
5
4
11
4
7
9
8
48
xM
fxM
fr
Fb
d) Notas de matemática de uma amostra com 51 alunos de uma mesma série:
i
1
2
3
4
5
6
7
NOTAS
[16 , 20[
[20 , 24[
[24 , 28[
[28 , 32[
[32 , 36[
[36 , 40[
[40 , 44[
TOTAIS ►
f
11
5
1
17
8
3
6
51
xM
fxM
fr
Fb