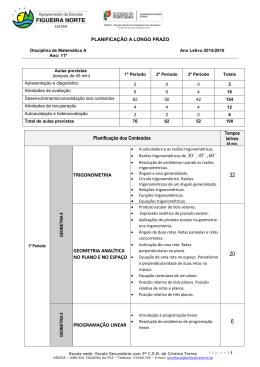
ESCOLA SECUNDÁRIA/3 DA RAINHA SANTA ISABEL – 402643
ESTREMOZ
Planificação anual de Matemática A – 11º ano
Ano Letivo 2015/2016
OBJETIVOS GERAIS
A – VALORES/ATITUDES
A1 – Desenvolver a autonomia e a solidariedade;
A2 – Desenvolver o espírito de tolerância e cooperação;
A3 – Manifestar hábitos de trabalho e persistência;
A4 – Desenvolver a confiança em si próprio;
A5 – Desenvolver o sentido de responsabilidade;
A6 – Desenvolver interesses culturais;
A7 – Reconhecer e manifestar interesse pela Matemática.
B – CAPACIDADES/APTIDÕES
B1 – Desenvolver o raciocínio e o pensamento matemático e científico;
B2 – Desenvolver a capacidade de utilizar a Matemática na interpretação e intervenção na vida real;
B3 – Desenvolver a capacidade de comunicação.
C – CONHECIMENTOS
C1 – Conhecer aspetos da história da Matemática;
C2 – Ampliar o conceito de número e desenvolver o cálculo;
C3 – Utilizar a calculadora para resolver problemas;
C4 – Ampliar o estudo da trigonometria;
C5 – Ampliar o estudo da geometria;
C6 – Ampliar o estudo de funções;
C7 – Iniciar o estudo das sucessões.
1
ESCOLA SECUNDÁRIA/3 DA RAINHA SANTA ISABEL – 402643
ESTREMOZ
Objetivos
Gerais
Conteúdos
Aulas
Previstas
1. Geometria no plano e no espaço II
1.1 Trigonometria
1.1.1 Resolução de problemas que envolvam triângulos.
Razões trigonométricas de um ângulo agudo.
1.1.2
Ângulo e arco generalizado. Radiano.
Expressão geral das amplitudes dos ângulos com os mesmos
lados, em graus e radianos.
Compreensão e utilização do círculo trigonométrico.
31
1.1.3 Funções seno, cosseno e tangente.
Definição; variação (estudo no círculo trigonométrico).
Comparação de senos e cossenos de dois números reais:
algumas relações (fórmulas) elementares;
1.1.4
Expressão geral das amplitudes dos ângulos com os
mesmos seno, cosseno ou tangente.
Equações trigonométricas elementares.
1º PERÍODO
A1 A2 A3 A4
A5 A6 A7
1.2 Geometria no plano e no espaço
B1 B2 B3
1.2.1 Produto escalar de dois vetores no plano e no espaço:
C1 C2 C3 C4
Definição e propriedades.
C5
Expressão do produto escalar nas coordenadas dos vetores
em referencial ortonormado.
1.2.2 Perpendicularidade de vetores e retas.
Equação cartesiana do plano definido por um ponto e o
vetor normal.
1.2.3 Interseção de planos e interpretação geométrica.
Resolução de sistemas.
Equações cartesianas da reta no espaço.
1.2.4
1.2.5
30
Paralelismo e perpendicularidade de retas e planos:
interpretação vetorial.
Programação linear. Breve introdução.
Domínios planos; interpretação geométrica de condições.
Testes, revisões, atividades de remediação, trabalhos e correções,
Autoavaliação.
13
74
TOTAL
2
ESCOLA SECUNDÁRIA/3 DA RAINHA SANTA ISABEL – 402643
ESTREMOZ
Objetivos
Gerais
Conteúdos
Aulas
Previstas
2. Introdução ao cálculo diferencial I. Funções racionais e com
radicais; Taxa de Variação e Derivada.
2.1 Estudo intuitivo das propriedades das funções e dos seus gráficos,
tanto a partir de um gráfico particular como usando calculadora
gráfica, para a classe de funções
𝑏
𝑓(𝑥) = 𝑎 +
𝑐𝑥 + 𝑑
2.2 Conceito intuitivo de limite, de +∞ e de −∞.
2.3 Noção de Taxa Média de Variação; cálculo TMV. Noção de Taxa de
Variação; obtenção da Taxa de Variação em casos simples.
2.4 Interpretação geométrica da Taxa de Variação.
Recorrendo à noção intuitiva de limite, definição de Derivada.
Determinação da derivada em casos simples.
2º PERÍODO
A1 A2 A3 A4 2.5 Propriedades que advêm do sinal da derivada, por constatação
A5 A6 A7
através de argumentos geométricos.
B1 B2 B3
C1 C2 C3 C6
2.6 Funções definidas por dois ou mais ramos.
48
2.7 Operações com funções: Soma, diferença, produto, quociente e
composição.
2.8 Função inversa de uma função. Funções com radicais quadráticos
ou cúbicos.
Operações com radicais quadráticos e cúbicos e com potências de
expoente fracionário.
Simplificação de expressões com radicais.
2.9 Resolução de problemas.
Testes, revisões, atividades de remediação, trabalhos e correções;
Autoavaliação.
12
TOTAL
60
3
ESCOLA SECUNDÁRIA/3 DA RAINHA SANTA ISABEL – 402643
ESTREMOZ
Objetivos
Gerais
Aulas
Previstas
Conteúdos
3. SUCESSÕES
3.1 Definição e diferentes formas de representação.
3.2 Estudo da monotonia e da limitação de uma sucessão.
3.3 Progressões aritméticas e geométricas: termo geral e soma de n
termos consecutivos.
1 𝑛
A1 A2 A3 A4
A5 A6 A7
B1 B2 B3
C1 C2 C3 C6 3.5 Limites.
C7
Infinitamente grandes e infinitamente pequenos.
Limites de sucessões e convergência. Noção de limite real.
38
3º PERÍODO
(1 + ) num contexto de
3.4 Estudo intuitivo da sucessão
𝑛
modelação matemática; primeira definição do número e.
3.6 A convergência das sucessões monótonas e limitadas.
3.7 Problemas de limites com progressões.
Testes, revisões, atividades de remediação, trabalhos e correções;
Autoavaliação.
12
TOTAL
50
Ao longo do ano letivo, consoante as necessidades e os conteúdos programáticos, serão focados temas
transversais, tais como:
1. Comunicação matemática.
2. Aplicações e modelação matemática.
3. História da matemática.
4. Lógica e raciocínio matemático.
5. Resolução de problemas e atividades de investigação.
6. Tecnologia e matemática
Esta planificação foi elaborada de acordo com o programa em vigor.
Professores a lecionar o 11ºano, Matemática A, em 2015/2016:


Amália Corrente
Francisco Serrano
4
ESCOLA SECUNDÁRIA/3 DA RAINHA SANTA ISABEL – 402643
ESTREMOZ
MATEMÁTICA A – 11º ANO
ANO LETIVO 2015/2016
PLANO DE UNIDADE I
GEOMETRIA NO PLANO E NO ESPAÇO I
Conteúdos
Aulas
previstas
Objetivos Específicos
TRIGONOMETRIA
Resolução de problemas
que envolvam triângulos.
 Procurar estratégias adequadas para determinar
distâncias a locais inacessíveis (alturas de edifícios,
etc).
 Identificar num triângulo retângulo as
trigonométricas dos seus ângulos agudos.
razões
 Deduzir as razões trigonométricas em 30º, 45º e 60º.
 Verificar as igualdades sen(α) = cos⁡(90° − α) e
cos(α) = sen⁡(90° − α).
6
 Conhecer as relações entre as razões trigonométricas
do mesmo ângulo (seno, cosseno e tangente).
 Determinar razões trigonométricas de um ângulo
agudo utilizando a calculadora.
Ângulo e arco generalizado:  Definir radiano.
 Desenhar um ângulo cuja amplitude seja um radiano.
 Desenhar arcos de circunferência de comprimento igual
ao raio.
 Converter graus em radianos. Converter radianos em
graus.
 Usar a calculadora para resolver problemas envolvendo
amplitudes de ângulos.
 Representar um ângulo num referencial ortonormado.
 Definir círculo trigonométrico.
 Associar a um ângulo um sentido.
 Identificar ângulos com o mesmo lado origem e o
mesmo lado extremidade.
 Determinar o comprimento de um arco de
circunferência conhecendo o raio e a amplitude do
ângulo ao centro correspondente.
 Resolver problemas usando áreas de setores circulares
5
8
ESCOLA SECUNDÁRIA/3 DA RAINHA SANTA ISABEL – 402643
ESTREMOZ
Conteúdos
Aulas
previstas
Objetivos Específicos
Funções seno, cosseno e  Definir as funções trigonométricas (seno, cosseno e
tangente).
tangente.
 Comparar senos e cossenos de dois números reais.
 Estudar a variação das funções trigonométricas no
círculo trigonométrico.
8
 Aplicar os conceitos de função periódica e de funções
trigonométricas
como
modelos
matemáticos
adequados a responder a problemas.
Expressão
geral
das  Verificar que se mantêm as relações:
amplitudes dos ângulos  tg⁡α = sen⁡α⁡ ; sen2 α + cos2 α = 1; 1 + tg 2 α = 1
cos α
cos2 α
com os mesmos seno,
cosseno
ou
tangente.  Definir as razões trigonométricas de um ângulo agudo
Equações trigonométricas no círculo trigonométrico.
elementares
 Reduzir um ângulo ao 1º quadrante.
 Definir as razões trigonométricas para um ângulo
qualquer.
 Resolver equações trigonométricas elementares.
9
 Definir as funções trigonométricas passando do círculo
trigonométrico para os pontos (𝑥, 𝑠𝑒𝑛⁡𝑥), por
exemplo, do plano cartesiano, usando atividades de
movimento circular.
GEOMETRIA NO PLANO E
NO ESPAÇO.
Produto escalar de dois  Relacionar o produto escalar com o trabalho em Física
vetores no plano e no
 Determinar o produto escalar de dois vetores no plano
espaço.
e no espaço
 Aplicar as propriedades do produto escalar
 Exprimir o produto escalar nas coordenadas dos
vetores
 Usar o produto
geométricos.
escalar
para
definir
lugares
 Resolver problemas usando conjuntos definidos por
condições
6
4
ESCOLA SECUNDÁRIA/3 DA RAINHA SANTA ISABEL – 402643
ESTREMOZ
Conteúdos
Objetivos Específicos
Perpendicularidade
de
 Determinar o ângulo de dois vetores do plano ou do
vetores e retas. Equação
espaço.
cartesiana
do
plano
definido por um ponto e o  Determinar o ângulo de duas retas no plano.
vetor normal.
 Determinar o ângulo de duas retas no espaço.
Aulas
previstas
4
 Relacionar o declive de uma reta com a sua inclinação.
 Relacionar o declive de duas retas paralelas ou
perpendiculares do plano.
 Escrever a equação de uma reta perpendicular a uma
reta dada, no plano.
 Resolver problemas usando perpendicularidade no
plano e no espaço.
 Escrever a equação de um plano definido por um ponto
e o vetor normal.
Interseção de planos e  Resolver sistemas de três equações com três incógnitas.
interpretação geométrica;
 Identificar as posições de planos definidos pelas suas
equações cartesianas da
equações.
reta no espaço.
 Determinar equações cartesianas de uma reta no
espaço.
Paralelismo e
perpendicularidade de retas  Aplicar o estudo da geometria analítica para
e planos.
determinar:
- a equação de um plano perpendicular a outro plano;
- a equação de um plano paralelo a outro plano;
- o ângulo de dois planos;
- o ângulo de uma reta com um plano;
 Determinar a interseção de duas retas no espaço
8
8
 Determinar a interseção de uma reta com um plano
 Resolver problemas utilizando a posição relativa de
planos, retas e planos e retas no espaço
Programação linear: breve  Resolver problemas simples utilizando programação
introdução.
linear.
7
6
ESCOLA SECUNDÁRIA/3 DA RAINHA SANTA ISABEL – 402643
ESTREMOZ
PLANO DE UNIDADE II
INTRODUÇÃO AO CÁLCULO DIFERENCIAL I. FUNÇÕES RACIONAIS E COM RADICAIS. TAXA DE VARIAÇÃO E DERIVADA
Conteúdos
Funções racionais
Aulas
previstas
Objetivos Específicos
 Estudar intuitivamente propriedades das funções e dos seus
gráficos.
𝑏
 Identificar funções racionais do tipo 𝑓 (𝑥) = 𝑎 + 𝑐𝑥+𝑑 .
 Determinar o domínio de funções racionais.
 Determinar as assimptotas horizontais e verticais de uma
função racional.
 Identificar funções racionais que têm uma assimptota
oblíqua.
10
 Interpretar o significado das assimptotas numa situação
concreta.
 Simplificar expressões algébricas.
 Resolver equações e inequações fraccionárias num contexto
de resolução de problemas.
Conceito intuitivo de  Estudar, intuitivamente e de forma experimental, o limite
de uma função num ponto, quando 𝑥 → +∞ e quando
limite, de +∞ e de −∞
𝑥 → −∞.
 Estudar transformações de funções racionais, confirmando
graficamente, e tirar conclusões sobre o limite no infinito
de uma função racional.
Operações com funções  Identificar funções iguais.
racionais e composição  Definir função soma, diferença, produto e quociente de duas
de funções envolvendo funções dadas.
polinómios do 2º e 3º
 Definir a função composta de duas funções.
grau
6
6
 Restrição de uma função a um intervalo.
Inversa de uma função.
 Definir a função inversa de uma função.
 Relacionar o gráfico de uma função com o gráfico da sua
inversa.
8
4
ESCOLA SECUNDÁRIA/3 DA RAINHA SANTA ISABEL – 402643
ESTREMOZ
Conteúdos
Objetivos Específicos
Aulas
previstas
 Identificar as funções irracionais.
Funções com radicais
quadráticos ou cúbicos  Estudar funções irracionais ligadas à geometria e em
contextos reais.
 Representar graficamente funções irracionais com
calculadora gráfica e/ou papel e lápis partindo do
conhecimento do gráfico de outras funções.
 Definir raiz de índice n na forma algébrica.
 Operar com radicais quadráticos e cúbicos e com potências
de expoente fracionário.
 Simplificar expressões com radicais, não incluindo a
racionalização.
11
 Resolver equações e inequações irracionais.
 Resolver problemas envolvendo funções irracionais.
 Fazer referência a hipérbole e suas propriedades (optativo).
 Determinar a equação reduzida da elipse recorrendo às
propriedades focais.
Taxa média de variação
 Dar significado a um número que corresponde à derivada de
uma função num ponto.
 Calcular a taxa de média variação.
 Interpretar a taxa média de variação no contexto de
problemas.
 Interpretar geometricamente a taxa de variação.
 Definir derivada de uma função num ponto recorrendo à
definição intuitiva de limite.
 Calcular a função derivada de algumas funções.
 Utilizar a calculadora gráfica para determinar a derivada de
uma função num ponto.
 Determinar a velocidade e a aceleração de um móvel
conhecida a lei do movimento.
 Relacionar a monotonia de uma função e o sinal da sua
derivada.
 Determinar extremos de uma função usando a derivada.
 Dar exemplos de funções que não têm derivada num ponto,
mas têm extremos nesse ponto.
 Resolver problemas de otimização usando abordagem
numérica, algébrica e gráfica.
9
11
ESCOLA SECUNDÁRIA/3 DA RAINHA SANTA ISABEL – 402643
ESTREMOZ
PLANO DE UNIDADE III
SUCESSÕES REAIS
Conteúdos
Aulas
previstas
Objetivos Específicos
A sucessão real como  Definir sucessão.
função
de
variável
 Utilizar diferentes formas de representar uma sucessão.
natural
 Conhecer a simbologia das sucessões.
 Escrever o termo geral de algumas sucessões em
situações muito simples.
 Calcular termos de uma sucessão.
4
 Usar a calculadora gráfica para representar sucessões.
 Representar graficamente uma sucessão definida por
recorrência.
 Estudar a monotonia de uma sucessão.
 Indicar majorantes e minorantes de um conjunto.
 Enquadrar um número.
 Mostrar que uma
enquadramentos.
Progressões aritméticas
sucessão
é
limitada
usando
 Identificar uma sucessão que seja uma progressão
aritmética
4
 Determinar o termo geral de uma progressão aritmética
 Calcular a soma de termos de uma progressão aritmética
Progressões geométricas
 Definir progressão geométrica
 Determinar o
geométrica
termo
geral
de
uma
progressão
 Calcular a soma de termos de uma progressão
geométrica
 Resolver problemas envolvendo progressões aritméticas
e geométricas
10
8
ESCOLA SECUNDÁRIA/3 DA RAINHA SANTA ISABEL – 402643
ESTREMOZ
Conteúdos
Aulas
previstas
Objetivos Específicos
Limites.
Infinitamente  Definir infinitamente grande positivo, negativo ou em
grandes e infinitamente
módulo
pequenos.
 Aplicar os conceitos de infinitamente grandes e
relacioná-los com os conceitos de monotonia e
limitação de uma sucessão
 Conhecer infinitamente grandes de referência e calcular
limites em casos simples usando os teoremas sobre
infinitamente grandes
6
 Definir infinitésimo
 Conhecer infinitésimos de referência e usá-los para
calcular limites em casos simples
 Aplicar os teoremas sobre infinitésimos
Limites de sucessões e  Aplicar teoremas sobre sucessões convergentes
convergências
 Calcular limites de sucessões convergentes aplicando os
teoremas clássicos
 Operar com sucessões divergentes
 Levantar indeterminações dos tipos
Convergência das
sucessões monótonas e
limitadas
∞
∞
e∞−∞
4
 Estudar a monotonia de uma sucessão
 Estudar a majoração e minoração de uma sucessão
 Identificar sucessões limitadas
 Utilizar o teorema das sucessões enquadradas
 Resolver problemas com limites de progressões
8
Estudo
intuitivo
da  Conhecer o número de Neper
sucessão de termo geral  Calcular limites que conduzam ao número de Neper
1
1 + num contexto de
𝑛
(Aplicar a matemática financeira ao cálculo de limites)
modelação matemática
Lógica e fundamentos
 Método de indução matemática
11
4