CAp/UERJ – Turma 1B – PROF. ILYDIO SÁ
1
CLASSIFICAÇÕES DAS FUNÇÕES
Classificação relativa ao conjunto contra-domínio
1 − Injetora
 2 − Sobrejetora


 3 − Bijetora
4 − Nenhuma das anteriores
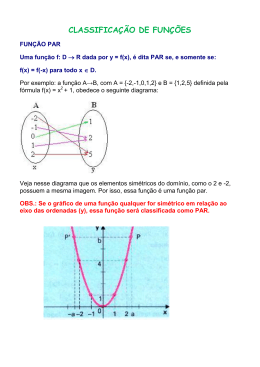
1 – INJETORA / INJETIVA
Para ser injetora ou injetiva, uma função deve obedecer à seguinte condição:
Dois elementos quaisquer do seu domínio nunca podem ser associados a um mesmo
elemento do contra-domínio.
Ex.
2 – SOBREJETORA / SOBREJETIVA
Para ser sobrejetora ou sobrejetiva, uma função deve obedecer à seguinte condição:
Nenhum elemento do contra-domínio pode ficar sem associação com qualquer dos
elementos do domínio.
Não pode sobrar elementos no contra-domínio sem associação. O conjunto-imagem é
igual ao contra-domínio.
Ex.
3 – BIJETORA / BIJETIVA
Para ser bijetora ou bijetiva, uma função deve obedecer ao mesmo tempo às condições
1 e 2 citadas anteriormente.
Assim, todo elemento do contra-domínio deve ser associado a um, e somente um,
elemento do domínio.
CAp/UERJ – Turma 1B – PROF. ILYDIO SÁ
2
4 – NENHUMA DAS ANTERIORES
Se uma função não obedece nem a condição 1 nem a condição 2 citadas anteriormente,
então ela não se classifica em nenhuma das opções anteriores.
A figura a seguir resume essa classificação apresentada:
Reconhecimento da injetividade e sobrejetividade através do gráfico
Para reconhecer se uma função representada através de um gráfico é ou não injetora,
basta traçar retas horizontais. Se, pelo menos, uma delas cortar a curva em mais de um
ponto, a função não será injetora. Já se todas as retas horizontais cortarem a curva da função
em apenas um ponto, então será injetora.
3
CAp/UERJ – Turma 1B – PROF. ILYDIO SÁ
Para reconhecer se uma função representada através de um gráfico é ou não sobrejetora,
basta identificar a imagem (I) através deste gráfico e comparar com o contra-domínio
(C.D) que deve ser dado. Se eles forem iguais ela será sobrejetora. Se existir elemento do
contra-domínio que não faz parte da imagem, então ela não será sobrejetora.
f: R→R
Ex. f : R → R y = 2x
y=x+1
I = R *+
C.D. = R
I ≠ C.D. → não é sobrejetora
I=R
C.D. = R
I = C.D. → é sobrejetora
FUNÇÃO INVERSA
Dada uma função bijetora f (x) qualquer com pares ordenados do tipo (a, b), a
função inversa f - 1(x) é uma função que fará o caminho inverso, ou seja, os pares
ordenados terão a forma (b, a).
Exemplo: Dada a função f : A → B, onde A = {2, 4, 7} e B = {3, 5, 8}, sua lei é dada por f
(x) = x + 1. Usando o diagrama de flechas:
f (x) → IDA
Pares ordenados
f = {(2, 3), (4, 5), (7, 8)}
f - 1 (x) → VOLTA
Pares ordenados
-1
f = {(3, 2), (5, 4), (8, 7)}
Regra Prática: Para achar a lei de associação para a função inversa f – 1 : B → A, basta
trocar x por y e vice-versa, para em seguida isolar a variável y. No nosso exemplo, a
nova lei será:
função original
função inversa:
Assim f - 1(x) = x – 1.
LEI DE ASSOCIAÇÃO
y=x+1
trocando x por y e vice-versa
x=y+1
isolando y:
y=x–1
PAR ORDENADO
f (4) = 5
(4,5)
f – 1 (5) = 4
(5,4)
4
CAp/UERJ – Turma 1B – PROF. ILYDIO SÁ
Uma função para ter uma função inversa deve ser bijetora. Caso contrário, quando fosse
feita a inversão do par ordenado, um mesmo elemento de B mandaria para mais de um
elemento de A se não fosse injetiva (figura da esquerda) ou um elemento de B ficaria sem
um correspondente se não fosse sobrejetiva (figurada direita).
Simetria existente entre uma função e a sua função inversa
Ao ser feita a inversão da função y = x , verifica-se que a função obtida (y = x) é
igual à própria função original. Essa função é chamada de função identidade e possui a
propriedade de ser a única função cuja inversa é ela mesma.
Do ponto de vista gráfico de uma função, essa função f (x) = x, funciona como um
eixo de simetria para qualquer função e sua inversa.
Veja o exemplo a seguir onde será feito o gráfico da função f (x) = 2x + 3 e a sua
x−3
, ambas funções de primeiro grau, crescentes.
função inversa f – 1 (x) =
2
f −1 ( x ) =
x−3
2
Observa-se que os pares ordenados (0, 3) e (-1,5; 0) da função f (x) = 2x + 3 foram
invertidos, obtendo os pares (3, 0) e (0; -1,5) da função inversa f – 1(x) = (x-3) / 2