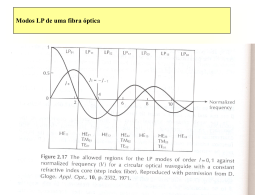
Parâmetros normalizados
Parâmetros normalizados

2
0

 ak0 n  n
U  a.u  a k .n  k
2
1


1
2 2
z
W  a.w  a k  n .k
Frequência normalizada

V  U W
2

1
2 2

V 2  a2 u 2  v2


1
2 2
2
2
1
k0 
 ak0 n1 2 
1
2

c
Constante de Propagação Normalizada
U 2 W 2 k z / k0   n22
b  1 2  2 
V
V
n12  n22
  1  k z / k0   n2
2
n1  n2
Contraste
n12  n22

2n12
  1  n2  n2
n1
NA  n  n
2
1

1
2 2
2
 n1 2 2 
1
V
k0 a
(abertura numérica)
2
z
2
0

1
2 2
2
Modo fundamental da fibra
Modo fundamental LP01
• Modo LP01 único modo em regime unimodal
• Frequência de corte nula VC = UC = 0
• Existe isolado na banda de frequências
• Equação característica
U
0 < V < 2.405
J1 (U )
K (W )
W 1
J 0 (U )
K 0 (W )
• Soluções aproximadas
Solução de Gloge
No intervalo 1.5 < V < 2.5
Solução de Rudolph/Neumann

U (V )  (1 2 )V 1 ( 4  V )


4 1/ 4 1
U (V )  V  (1.1428V  0.996)
2

2 1/ 2
Dispersão dos modos LP de uma fibra óptica
Distribuição de potência na Fibra
Distribuição de potência na fibra óptica
•
A potência transportada pela FO está
distribuida no núcleo e na baínha
•
Factor de confinamento de potência 

Pnúcleo
1  d (bV ) 
 b 
Pnúcleo  Pbaínha 2 
dV 
Γ = 1 - U2 /V2 = 0.1
(a)
(b)
(a) U2 /V2 = 0.1 ou Γ = 0.9
(b) U2 /V2 = 0.9
ou
Γ = 0.1
(a)
(b)
Capacidade de transmitir informação
Largura de banda
Transmissão do sinal na Fibra Óptica limitada por
Atenuação
Dispersão
Capacidade de transmitir informação
•
Capacidade  taxa máxima de transmissão fiável
•
C = B log2 (1 + S/N)
•
•
B – largura de banda do canal
BT - ritmo de transmissão máximo
[Lei de Shannon]
BT ~ 2 B
Para transmitir ao ritmo BT ~ é necessário um canal com uma largura de banda
B = BT /2 (código NRZ) ou B = BT (código RZ).
Distorsão do sinal - aumenta com B e L
B – ritmo de transmissão
L – espaçamento entre repetidores
Capacidade de um sistema de comunicação
Mede-se produto BL
1970 – 100 Mb/s – km
2000- > 10 12 Mb/s – km
Regime multimodal (descrição da óptica geométrica)
Dispersão intermodal
n2
∟'
Øt
Øi
n1
Өi
∟
Raios meridionais
a) Velocidade máxima: modo cujos raios são praticamente axiais.
b) Velocidade mínima: modo cujos raios incidem na interface núcleo/baínha segundo


iL  i  sin 1 n12  n 2

2


L
a) Raio axial t min  n1
c
b) Raio meridional extremo
2
L'
L / cost L
L n1
t máx 
n1 
n1 
c
c
c n2
2
Ritmo de transmissão
• A dispersão intermodal conduz ao espraiamento dos impulsos transmitidos o que se
traduz na diminuição do ritmo de transmissão
• Impulso de duração 2 Δtc →
Ritmo de transmissão máximo:
B
1
2t c
• Soluções para reduzir/eliminar dispersão intermodal:
a) Fibras de núcleo não homogéneo
b) Fibras monomodo
Fibra multimodal
t 
 L  n  n2
L  n1
n1 
 1  n1  1
c  n2
 c  n2



1

L
n1

c
ρ
Perfil gradual
n (ρ)
Perfil parabólico
n1 2
t  L
c 2
Fibra monomodal
Tempo de transmissão do sinal:
• Para reduzir/eliminar a dispersão intermodal: t 
- utilizam-se fibras ópticas unimodais
L
vg
- utilizam-se fibras ópticas multimodais com índice de refracção variável n1 (ρ).
• A velocidade de propagação aumenta com ρ porque n1 diminue com ρ, o que compensa os
percursos maiores a percorrer pelos raios associados aos modos de ordem superior.
Mecanismos de dispersão da fibra óptica
•
O PCM (Pulse Code Modulation) é um dos métodos usados em sistemas de comunicação com
fibras ópticas para modular a luz portadora.
•
A diferença (dispersão) dos tempos de grupo 
 das várias componentes espectrais
L
t 

contidas no impulso, dá origem à sua distorção.
 g vg 


Dispersão intermodal
Ocorre em fibras a operar em regime multimodal. Os modos apresentam vg diferentes
(excepto quando são degenerados).
Dispersão material
O índice de refracção da fibra, n1, varia com ω.
Dispersão estrutural
Dispersão do guia de ondas (estrutura dieléctrica que guia as ondas).
•
As dispersões material e estrutural estão presentes quer em fibras em regime unimodal
quer em regime multimodal e são ambas proporcionais à largura de banda do impulso
transmitido.
Dispersão material - Alargamento do impulso
•
Dispersão traduzida na eq. característica:
•
Atraso de grupo por unidade de comprimento:
tg
L

vf 
D (ω, kz) = 0
1
vg

kz

c
n
e
vg 

c

k z ng
t g   
Δ λ << λ0
λ
λ0
L
ng  
c
Indice de grupo
Dispersão estrutural
• É intrínseca a todos os sistemas de propagação guiada. Traduz a dependência de λ
das constantes de propagação no núcleo e na baínha.
• A dispersão estrutural só é relevante em fibras monomodo para regiões de λ em que
o coeficiente de dispersão material se aproxima de zero (ex: λ ═ 1300 nm)
n2 
d 2 bV 
g1
Me 
V
c 0 n
d V2
Dependência de alguns parâmetros modais com a frequência (normalizada)
t
Confinamento de potência
Dispersão estrutural
.
Dispersão material
t 
dtg

d
L dng  
t 
  M L 
c d
Largura espectral
Coeficiente de dispersão
Alargamento do impulso
•
O coeficiente de dispersão M caracteriza o alargamento do impulso
devido às variações do índice de refração do núcleo (sílica) com o
comprimento de onda (ω).
Atenuação
1ª geração  ~0.8 m
2ª geração  ~ 1.3 m 3ª geração  ~ 1.55 m
4ª geração aumento B multiplexagem; amplificação óptica 1500 km 2Gb/s
5ª geração propagação de solitões 12 000 km 2.4 Gb/s (experimental)
Espaçamento L entre repetidores
a) Influência da atenuação
L
Pin
Prec  Pin e2L
  ctede atenuação
•
Atenuação ═> Amplificação
b) Distorção dispersiva
═> Regeneração (da forma do sinal)
a) Atenuação
Prec = Fs n h f BT
n – nº de fotões que o receptor precisa para detectar 1 bit
hf – energia de um fotão (h-cte Planck, 6.626 ×10-34 Js)
Bt – ritmo de transmissão
Fs – factor de segurança (Fs > 1)
B0 – ritmo de transmissão de referência (bits/s)
Prec  Pin  2L  Fs nhf B0
BT
B0
 F nhf B0 
B 
  ln  T 
 2L  ln  s
P
 B0 
in

 2 L0
L0 – espaçamento associado ao ritmo de referência B0.
L  L0 
1  BT 
 m
ln 
2  B0 
L
BT  L 
Variação lenta
L0
B0
BT
Espaçamento entre repetidores:
atenuação e distorção
L (log)
B (log)
•
A conjugação dos efeitos devidos à atenuação e á distorção conduz aos seguintes resultados:
- a atenuação é o factor limitativo para os ritmos de transmissão baixos.
- a distorção é o factor limitativo para os ritmos de transmissão altos.