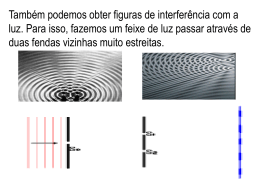
I- INTRODUÇÃO
1- Luz
• A luz é uma onda eletromagnética
sensibilizar nossos órgãos visuais
capaz de
2- Raio de luz: linha orientada que representa,
graficamente, a direção e o sentido de propagação da luz.
3- Feixe de luz: conjunto de raios de luz.
4- Fonte de Luz: todo corpo capaz de emitir luz.
a- Fonte Primária: emite luz própria (corpos luminosos).
-Incandescente – quando emite luz a alta temperatura.
Exemplo: lâmpada incandescente, a temperatura do
filamento chega a cerca de 2 500 0C.
-Luminescente – quando emite luz a temperatura
relativamente baixa. Exemplo: vaga-lume, lâmpadas
fluorescentes, objetos fosforescentes (como interruptor de
luz, mostrado de alguns relógios etc.).
b- Fonte Secundária: emite luz que recebe de outro
corpo (corpos iluminados).
5- Meios de propagação da luz
a- Meio Transparente: permite a propagação da luz
através de si, segundo trajetórias regulares, permitindo a
visão nítida dos objetos (vidro comum, ar).
b- Meio Translúcido: permite a propagação da luz
através de si, segundo trajetória irregular, não permitindo
a visão nítida dos objetos (vidro fosco, papel de seda).
c- Meio Opaco: Não permite a propagação da luz
através de si (madeira e parede de tijolos).
6- Tipos de meios ópticos:
a- Meio Homogêneo: É aquele apresenta as mesmas
propriedades físicas em toda a sua extensão.
b- Meio Isótropo: É aquele no qual a luz se propaga
com a mesma velocidade em todas as direções e
sentidos.
II - REFLEXÃO DA LUZ E ESPELHO PLANO
1- TIPOS DE REFLEXÃO
a) Reflexão especular
Ocorre em superfícies polidas (bem lisas). Aqui a
forma do pincel de luz não é destruída depois da
reflexão.
b) Reflexão difusa
Ocorre
em
superfícies
rugosas
(cheias
de
irregularidades). Aqui a forma do pincel de luz é
destruída depois da reflexão, ou seja, a luz acaba
sendo espalhada para várias direções. Veja a figura
abaixo:
2- LEIS DA REFLEXÃO
1° Lei: “o raio incidente R, a normal N e o raio
refletido R’ são coplanares.”
2° Lei: “o ângulo de reflexão r é igual ao ângulo de
incidência i.”
III- Refração
Obs.: A refração sempre
vem acompanhada da
reflexão
1- ÍNDICE DE REFRAÇÃO ABSOLUTO
é a razão entre a velocidade da luz no vácuo e a
velocidade da luz no meio considerado.
nmeio
C

Vmeio
onde C  3  108 m s  3  105 Km / s
nvácuo  1

nar  1
n
 demais meios  1
Então, quanto maior for o índice de refração de uma
substância, maior será sua refringência, ou seja, mais
dificuldades a luz encontrará para atravessar seu
interior. Por isso sua velocidade será irá diminuir.
menor velocidade

meio mais refringente (  )  
 menor comprimento de onda

maior velocidade

meio menos refringente ()  
 maior comprimento de onda

2- ÍNDICE DE REFRAÇÃO RELATIVO
• O índice de refração do meio
A em relação ao meio B, é
definido por:
nA,B
nA v B


nB v A
ou
nB,A
nB v A


nA v B
nA,B
C
nA v A v B



C vA
nB
vB
3- LEIS DA REFRAÇÃO
1ª Lei : o raio incidente, a reta normal e o raio
refratado deverão estar contidos sempre num
mesmo plano.
2ª Lei : Existe uma relação entre os ângulos de
incidência e de refração de um raio de luz. Esta
relação é representada pela Lei de SnellDescartes.
Lei de Snell-Descartes
𝑛𝐴 𝑠𝑒𝑛𝑖 = 𝑛𝐵 𝑠𝑒𝑛𝑟
n
n
B
A
VA
sen iˆ A



VB
sen rˆ B
4- PROPRIEDADES DA REFRAÇÃO
1ª) n1 < n2  Quando a luz passa do meio menos
refringente para o meio mais refringente, a velocidade
de propagação da luz diminui e o raio de luz se
aproxima da normal, para incidência oblíqua.
Raio
incidente
Normal
i
A
B
VB  VA

    λB  λA

rˆ  iˆ ( se iˆ  0)
r
Raio
refratado
Neste caso podemos dizer que o raio refratado aproxima-se da normal
2ª) n1 > n2  Quando a luz passa do meio mais
refringente para o meio menos refringente, a velocidade
de propagação da luz aumenta e o raio de luz se afasta
da normal, para incidência oblíqua.
Raio
incidente
Normal
i
A
B
r
Raio
refratado
VB  VA

    λB  λA

rˆ  iˆ ( se iˆ  0)
Neste caso podemos dizer que o raio refratado afasta-se da normal
OBS- Se a luz incidir normalmente à superfície de
separação de dois meios, a luz não se desvia.
Normal
i=0º
Raio
incidente
A
B
r=0º
VB  VA

    λB  λA

o
ˆ
ˆ
r

i

0

Raio
refratado
Neste caso tivemos uma refração sem desvio
Continuidade Óptica
5- ÂNGULO LIMITE E REFLEXÃO INTERNA TOTAL
a- REFLEXÃO INTERNA TOTAL: Para ocorrer reflexão
total a luz deve se propagar no sentido do meio mais
para o meio menos refringente (nB>nA) o ângulo de
incidência i deve superar o ângulo limite L.
N
N
N
n
r=0o
i=0o
N
i>L
Neste caso tivemos
uma reflexão total
i=L
i<L
b- Cálculo do ângulo limite ( L ).
Raio
incidente
Normal
B
i= L
A
r= 90º
Raio
refratado
nA .sen 90  nB .sen L
0
nA
senL 
nB
ou
nmenor
senL 
nmaior
Prismas de Reflexão Total
Prisma de Amici
Prisma de Porro
i
i
i›L
6. APLICAÇÃO DA REFLEXÃO TOTAL
Fibra Ótica
FUNCIONAMENTO DA FIBRA ÓTICA
ar
i>L
casca
núcleo

casca
ar
Miragem
MIRAGEM
I<L
Ar frio
I<L
I>L
Reflexão
total
Ar quente
Ar mais quente
Ar muito quente
Asfalto
ALTURA APARENTE DOS ASTROS
A densidade do ar diminui com a altura
• A densidade do ar diminui com a altura. Observe
esquema a seguir:
Imagem
Objeto
7- Luz monocromática e Luz policromática
a- Luz Monocromática: constituída de uma única cor,
como por exemplo a luz monocromática amarela emitida
pelo vapor de sódio, nas lâmpadas.
b- Luz policromática: constituída de duas ou mais cores,
como por exemplo a luz branca do Sol.
A luz do sol (ou das lâmpadas comuns) é chamada de
luz branca, pois ao incidir sobre uma das faces de um
prisma de vidro, decompõe-se em sete cores
fundamentais: vermelha, alaranjada, amarela, verde, azul,
anil e violeta.
8. DISPERSÃO
Vermelho
Alaranjado
Amarelo
Verde
Azul
Anil
violeta
v
f
n
Dispersão da luz Branca
DISPERSÃO
Dentro do prisma a cor
violeta possui a menor
velocidade.(Violenta é
a cor mais LENTA.)
n(vermelho) < n(violeta)
v(vermelho) > v(violeta)
Desvio(vermelho) < Desvio(violeta)
9. Polarização:
Uma onda natural (não polarizada) é aquela que possui
várias direções de vibração, em relação a direção de
propagação. Polarizar uma onda é fazê-la vibrar em uma
única direção. A polarização é exclusiva das ondas
transversais, não ocorrendo esse fenômeno com as ondas
longitudinais.
Polarização horizontal
Polarização vertical
Apenas as ondas
transversais podem
ser polarizadas.
Pode obter-se facilmente luz polarizada utilizando
placas polaróide.
Duas placas cruzadas não deixam passar a luz.
A primeira placa polariza a luz
que não passa na segunda
placa por estar cruzada.
Descrição de uma onda progressiva
Define-se a direção de polarização da onda
eletromagnética (OEM) como a direção do vetor campo
elétrico, ao qual a maioria dos detectores de radiação
eletromagnéticas são sensíveis. Exemplo:
𝐸 = 𝑗𝐸0 cos 𝑘𝑥 − 𝜔𝑡
𝐵 = 𝑘 𝐵0 cos 𝑘𝑥 − 𝜔𝑡
OEM polarizada na direção y. O campo elétrico tem
apenas componente y.
1
𝑐=
𝜇0 𝜖0
No vácuo, todas as OEM possuem
a mesma velocidade c 3.108 m/s
y
E
x
z
B
k
2

2

 2
T
c

k

1
 0 0
Luz Polarizada
A maioria das OEM produzidas por uma única fonte são
polarizadas. Entretanto, nas fontes comuns de luz (Sol,
lâmpada fluorescente), os radiadores, que são os átomos
constituintes da fonte, atuam independentemente uns
dos outros. Como consequência, a luz emitida consiste
de várias ondas independentes cujos planos de vibração
se acham orientados aleatoriamente. Dizemos que essas
ondas são não polarizadas.
Polarizador
Podemos transformar luz originalmente não-polarizada
em luz polarizada fazendo-a passar por uma placa
polarizadora.
No plano da placa existe uma direção característica
chamada direção de polarização.
Apenas os componentes dos vetores paralelos à direção
de polarização são transmitidos.
Os componentes perpendiculares são absorvidos.
Polarizador ideal: transmite 100% da luz na direção
de polarização e bloqueia totalmente a luz na direção
perpendicular.
Polarizador real: aproximadamente
transmissão e 99% de bloqueio.
80%
de
Intensidade da luz após atravessar um
polarizador
Quando se faz passar luz não-polarizada através de um
polarizador, a intensidade transmitida é metade da
intensidade original
Intensidade da luz após atravessar um
polarizador
Lei de Malus
Qual a intensidade da luz polarizada que é transmitida
por um polarizador, cujo eixo de polarização está girado
de um ângulo  em relação ao da luz incidente ?
luz não
polarizada
direção de
polarização
I=?
luz polarizada
intensidade Im
Lei de Malus
E y  Em cos 
I α E y2  Em2 cos 2 
I  I m cos 
2
Lei de Malus
Lei de Malus – 3 Polarizadores
luz não
polarizada
direção de
polarização
45o
90o
I
I0
I0
I1 
2
Intensidades
I 2  I1 cos2 45o
I3  I 2 cos2 45o
Luz não-polarizada atravessa
um polarizador:
luz não
polarizada
intensidade Im
Luz polarizada atravessa
um polarizador:

luz
polarizada
Im
y

luz
polarizada
Im
I 
2
I  I m cos 
2
Lei de Malus
x
Aplicações
LCD (Liquid Crystal Display)
O cristal líquido é colocado entre polarizadores
cruzados. Um campo elétrico aplicado às moléculas do
cristal muda a direção de polarização, e a luz é
bloqueada no segundo polarizador.
Há substâncias com atividade óptica, isto é, que
fazem rodar o plano de polarização da luz polarizada
linearmente.
Observador
O plano de
polarização
rodou
Substância opticamente
ativa
Luz polarizada
Rotação, 
À entrada
À saída
Rotação, 
Rotação negativa
Substâncias
levógiras, l
Rotação positiva
Substâncias
dextrógiras, d
Tipos de polarização
1. Polarização linear: o campo elétrico permanece
sempre no mesmo plano.
2. Polarização circular: o campo elétrico (e magnético)
permanecem constantes em magnitude, mas giram ao
redor da direção de propagação.
3. Polarização elíptica: a amplitude das componentes
ortogonais do campo elétrico são diferentes.
Polarização por reflexão
• Não é eficiente pois somente uma fração da luz
incidente é refletida por uma superfície.
• O “reflexo” em uma superfície é polarizado
horizontalmente.
• Óculos com filtros polarizadores verticais eliminam
a maior parte dos reflexos em superfícies.
Espalhamento Rayleigh
onda incidente
não polarizada
ondas
espalhadas
A luz espalhada na
direção perpendicular à
da luz incidente é
polarizada.
A luz espalhada nas
outras direções é
parcialmente polarizada.
molécula
Foto: R. Holle
Por que o céu é azul?
... vandaar dat de horizon-hemel vaak
Por que o céu não é escuro fora da direção do Sol?
witter is dan de zenith-hemel.
Por que o céu não é escuro fora da direção
do Sol ?
A Terra vista do espaço.
A Lua vista do espaço, sobre a
atmosfera da Terra.
O céu é escuro fora da direção do Sol …
… na ausência de atmosfera !
H.E. Edens, www.weather-photography.com
Por que os pores-do-sol são avermelhados ?
De kleur van de ondergaande zon hangt
af van de deeltjes in de atmosfeer: hoe
Espalhamento Rayleigh
Espalhamento de luz por moléculas com diâmetro
d << 
Intensidade 
1
4
Luz de pequeno comprimento de onda (azul) é espalhada
mais eficientemente que a de grande comprimento de
onda (vermelha).
Demonstração da lei de Snell
• usando o princípio de Huygens
• usando o princípio de Fermat
Frente de Onda e Raio de Onda
Frente de Onda: é a fronteira entre a região atingida
pela onda e a região ainda não atingida.
Raio de Onda: é uma linha orientada que tem origem
na fonte de onda e é perpendicular às frentes de
onda. Os raios de onda indicam a direção e o sentido
de propagação das ondas num meio.
Princípio de Huygens
Todos os pontos de uma frente de onda podem ser
considerados como fontes de onda secundárias que se
espalham pra fora com uma velocidade igual à
velocidade de propagação da onda.
Princípio de Huygens
Num certo intervalo de tempo
t, a onda se desloca de AA’ até
BB
Meio 1
n1
1
A
Meio 2 n2
n2>n1
2
B
percorrido no meio 1, com velocidade
v1. Então:
AB  v 2 t
A' B' v1

AB v 2
Pela figura vemos que:
B’
2
com velocidade v2 e o trecho A’B’ é
A' B'  v1t
A’
1
O trecho AB é percorrido no meio 2,
A' B'
sen 1 
AB'
AB
sen 2 
AB'
sen 1 A' B' v1


sen2
AB v 2
Como n1 = c / v1 e n2 = c / v2
n1sen 1  n 2sen 2
Princípio de Fermat
Quando um raio de luz propaga-se entre dois pontos P e P’
quaisquer, a trajetória seguida é aquela que requer o
menor tempo de percurso
v1=c/n1, v2=c/n2
r1= distância percorrida no meio 1
d
P
r2=distância percorrida no meio 2
r1
1
Tempo total para percurso PP’=t
1
a
n1
x
d-x
r2
n2
2
b
2
P’
b 2  (d  x ) 2
r1 r2
a2  x2
t  

v1 v 2
c / n1
c / n2
Escolhendo diferentes valores de x,
pode-se tomar diferentes trajetórias
entre P e P’
Princípio de Fermat
Para obter o tempo mínimo vamos derivar a expressão
anterior, em relação a x, e igualar a derivada a zero;
Pela figura:






1/ 2
dt n1 d 2 2 1/ 2 n 2 d 2

a x

b  (d  x ) 2
dx c dx
c dx
n1  1 
2x
n 2  1  2(d  x ) 1
  
  
1/ 2
2
2
c 2 a x
c  2  b 2  (d  x ) 2 1 / 2


dt
n1 x
n2 ( d  x )


0
1/ 2
1/ 2
2
2
2
2
dx c a  x
c b ( d  x )




sen1 
x
x
 2 2 1/ 2
r1 ( a  x )
dx
dx
sen 2 
 2
r2
( b  ( d  x )2 )1 / 2
n1sen1  n 2sen2
Dioptro plano – Profundidade aparente
observador
2
1
imagem
objeto
Lâminas de faces paralelas
i
AR
i-r
A
VIDRO
r
D
e
d
AR
Calculando o deslocamento lateral
B
d
C
PRISMA
A: ângulo de abertura do prisma
i1: ângulo de incidência na 1ª face
r1: ângulo de refração na 1ª face
r2: ângulo de incidência na 2ª face
i2: ângulo de refração na 2ª face
Equações do prisma