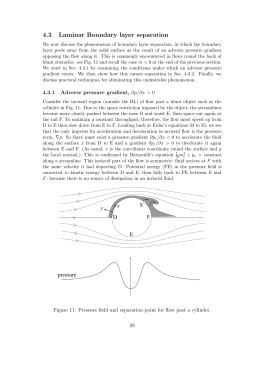
Introduction to the Boundary Layer
concept

Content:
–
–
–
–
–
–
–
2004
Introduction to the Bounday Layer concept;
Constraint and unconstraint boundary layers
Free shear flows and wakes
Laminar and turbulent boundary layers;
Boundary layer separation;
Thin boundary layer equations
Longitudinal pressure gradient effects on the boundary layer
growth.
Mecânica dos Fluidos II
Prof. António Sarmento - DEM/IST
Introduction to the Boundary Layer
Movies (6), 88, 89
MFM: BL, Impulsive Started Flow, Overview
MFM: BL, BL Concepts,Viscous effects near boundaries
2004
Mecânica dos Fluidos II
Prof. António Sarmento - DEM/IST
Introduction to the Boundary Layer
 Boundary
layer: flow region in the vicinity of a wall
where viscous/diffusive effects and energy dissipation
are significative.
Outer invisicid flow
y
U
U
x
d(x)
Boundary layer width:
u(d)=0,99 U
2004
Mecânica dos Fluidos II
Boundary layer: u y significant
Prof. António Sarmento - DEM/IST
Introduction to the Boundary Layer
 Streamlines
y
U
over a flat plat
Limit strealine of Boundary layer
U
Streamlines
x
1. The streamlines moves away slowly from the wall. Why?
2. This separation of streamlines is most intense outside the
boundary layer. Why?
2004
Mecânica dos Fluidos II
Prof. António Sarmento - DEM/IST
Introduction to the Boundary Layer
 Notes
about boundary layer:
1. The boundary layer may be laminar or turbulent
2. Thin boundary layer if d(x)<<x
3. Boundary layer confined: cannot grow free (ex: tube or
between plates)
2004
Mecânica dos Fluidos II
Prof. António Sarmento - DEM/IST
Introduction to the Boundary Layer
 Constrained
External
Flow
d(x)
Boundary Layer:
Boundary
Layer
Fully Developed
Entrance Region Velocity Profiel
1. Entrance region: the velocity increases at the center line (to keep the
mass flow rate) and the pressure falls (Bernoulli’s Equation)–> dp/dx<0.
2. After the union of all boundary layers, all the flow is boundary
layer flow d. (x )  R
In turbulent flow, the eddy dimension is limited by d.
2004
Mecânica dos Fluidos II
Prof. António Sarmento - DEM/IST
Introduction to the Boundary Layer
 Boundary
layer in external flows (unconstrained)
1. d is not limited, it grows with the distance to the leading edge x
(beginning).
2. Nondimensional velocity profile can stabilize
2004
Mecânica dos Fluidos II
Prof. António Sarmento - DEM/IST
Introduction to the Boundary Layer
 Shear
flows (longitudinal convective transport of momentum
affected by diffusion):
2004
o
Free Shear Flows: ex: free jet
o
Wake: flow zone resulting from the joining of
the boundary layers on the two faces of the
plate
Mecânica dos Fluidos II
Prof. António Sarmento - DEM/IST
Introduction to the Boundary Layer
 Transition
from laminar to turbulent:
inertialforces Ux
Re =
=
viscousforces 
•Start of BL:
x=0
x – Start of Boundary Layer (BL)
Re = 0
Laminar
Flow
 0 =  (u y)y=0 Very high
•Long plate:
Transition to
turbulent
2004
Critical Re
(5105)
Mecânica dos Fluidos II
Re increases
 0 =  (u y)y=0 decreases
Prof. António Sarmento - DEM/IST
Introduction to the Boundary Layer
 Regions
–
–
–
–
of turbulent boundary layer:
Linear sub-layer or laminar sub-layer;
Transition layer;
Logaritmical profile zone;
Outer zone (turbulent vorticity and non turbulent
outer flow).
mfm – BL/ Instability, Transition and Turbulence:
Boundary Layer transition
Fully turbulent BL flow
Instability and transition in pipe and duct flow
Fully turbulent duct flow
2004
Mecânica dos Fluidos II
Prof. António Sarmento - DEM/IST
Laminar Thin Boundary Layer Equations
(d<<x) over flat plate
flow, r e  constants.
p y  0 Streamlines slightly divergents
p x  dpe dx
 Steady

 2D
Navier-Stokes Equations at x direction:
u
u
1 p   2u  2u 
u v
=
   2  2 
x
y
r x  x y 
dpe dx
2004
Mecânica dos Fluidos II
 2u
Compared with
y 2
Prof. António Sarmento - DEM/IST
Laminar Thin Boundary Layer Equations
(d<<x) over flat plate
 Laminar
thin boundary layer equations (d<<x) to
flat plates
u
u
1 dpe
 2u
u v
=
 2
x
y
r dx
y
pe external pressure, can be calculated bu Bernoulli’s Equation
because there is not viscous effects outer the Boundary Layer
Note 1. The plate is considered flat if d is lower then the local
curvature radius
Note 2. At the separation point, the BD grows a lot and no longer
thin
2004
Mecânica dos Fluidos II
Prof. António Sarmento - DEM/IST
Turbulent Thin Boundary Layer
Equations (d<<x) over flat plate
 2D
Thin Turbulent Boundary Layer Equation
(d<<x) to flat plates:
u
u
1 dpe
 2u  uu uv uw 

u
v
=
 2  


x
y
r dx
y  x
y
z 
0
0
Resulting from
Reynolds Tensions
(note the w term)
2004
Mecânica dos Fluidos II
Prof. António Sarmento - DEM/IST
Boundary Layer Separation
 Boundary
Layer Separation: reversal of the flow by
the action of an adverse pressure gradient (pressure
increases in flow’s direction) + viscous effects
mfm: BL / Separation / Flow
over edges and blunt bodies
2004
Mecânica dos Fluidos II
Prof. António Sarmento - DEM/IST
Boundary Layer Separation
 Boundary
layer separation: reversal of the flow by the
action of an adverse pressure gradient (pressure increases
in flow’s direction) + viscous effects
2004
Mecânica dos Fluidos II
Prof. António Sarmento - DEM/IST
Boundary Layer Separation
 Bidimensional
(2D) Thin Boundary Layer (d<<x)
Equations to flat plates:
u
u
1 dpe
 2u
u v
=
 2
x
y
r dx
y

Close to the wall (y=0)
u=v=0 :
  2u 
1 dpe
 2  =
 y  y =0  dx

2004
Similar results to turbulent boundary layer - close to
the wall there is laminar/linear sub-layer region.
Mecânica dos Fluidos II
Prof. António Sarmento - DEM/IST
Boundary Layer Separation
 Outside
 Close
 2u
0
2
y
Boundary layer:
to the wall (y=0)
u=v=0 :
  2u 
1 dpe
 2  =
 y  y =0  dx
 The
external pressure gradient can be:
o
dpe/dx=0 <–> U0 constant (Paralell outer streamlines):
o
dpe/dx>0 <–> U0 decreases (Divergent outer streamlines):
dpe/dx<0 <–> U0 increases (Convergent outer streamlines):
o
2004
Same sign
Mecânica dos Fluidos II
Prof. António Sarmento - DEM/IST
Boundary Layer Separation
 Zero
pressure gradient:
dpe/dx=0 <–> U0 constant (Paralell outer streamlines):
  2u 
 2   0
 y  y =d
y
u
Curvature of velocity
profile is constant
No separation of boundary
layer
  2u 
 2  = 0
 y  y =0
Inflection point at the wall
2004
Mecânica dos Fluidos II
Prof. António Sarmento - DEM/IST
Boundary Layer Separation
 Favourable
pressure gradient:
dpe/dx<0 <–> U0 increases (Convergent outer streamlines):
  2u 
 2   0
 y  y =d
y
No boundary layer
separation
  2u 
 2   0
 y  y =0
2004
Curvature of velocity profile
remains constant
Mecânica dos Fluidos II
Prof. António Sarmento - DEM/IST
Boundary Layer Separation
 Adverse
pressure gradient:
dpe/dx>0 <–> U0 decreases (Divergent outer streamlines):
  2u 
 2   0
 y  y =d
y
Boundary layer
Separation can occur
  2u 
 2   0
 y  y =0
P.I.
Curvature of velocity
profile can change
Separated Boundary Layer
2004
Mecânica dos Fluidos II
Prof. António Sarmento - DEM/IST
Boundary Layer Separation
 Sum
of viscous forces:
 2u
 2
y
Become zero with velocity
Can not cause by itself the fluid stagnation (and
the separation of Boundary Layer)
2004
Mecânica dos Fluidos II
Prof. António Sarmento - DEM/IST
Boundary Layer Separation

Effect of longitudinal pressure gradient:
dpe
0
dx
(Convergent outer
streamlines)
dpe
 0 (Divergent outer
streamlines)
dx
Viscous effects retarded
Viscous effects reinforced
u
1 1 dpe
=
 ...
Fuller velocity
x
u r dx
Less full velocity
profiles
profiles
Decreases BL growth
2004
Mecânica dos Fluidos II
Increases BL growths
Prof. António Sarmento - DEM/IST
Boundary Layer Separation

Effect of longitudinal pressure gradient:
Fuller velocity
profiles
u
1 1 dpe
=
 ...
x
u r dx
Less full velocity
profiles
Decreases BL growth
Increases BL growths
Fuller velocity profiles – more resistant
to adverse pressure gradients
Turbulent flows (fuller profiles)- more resistant to
adverse pressure gradients
2004
Mecânica dos Fluidos II
Prof. António Sarmento - DEM/IST
Boundary Layer Sepaation
Longitudinal and intense adverse pressure gradient does
not cause separation
=> there’s not viscous forces
2004
Mecânica dos Fluidos II
Prof. António Sarmento - DEM/IST
Boundary Layer Separation

No viscous forces – no separation of Boundary Layer:
dV 1 dp
V
=
ds r ds
(ds displacement over a
streamline)
dp
V=0 (stagnation point)
=0
ds
No reversal of
the flow
2004
Mecânica dos Fluidos II
From pressure forces
Prof. António Sarmento - DEM/IST
MECÂNICA DOS FLUIDOS II

Contents:
–
–
–
–
–
–
–
–
–
2004
Boundary Layer;
Boundary Layer thickness;
Limiting line of Boundary Layer;
Deviation of streamlines at Boundary Layer;
Thin Boundary Layer;
Constrained and unconstrained boundary layer;
Free Shear flows;
Wakes;
Thin boundary layer equations.
Mecânica dos Fluidos II
Prof. António Sarmento - DEM/IST
Separação da Camada limite

Contents:
– Boundary Layer Separation: conditions to separation
– Adverse, favourable and zero pressure gradient;
– Effects of pressure gradient on the Boundary layer evolution
2004
Mecânica dos Fluidos II
Prof. António Sarmento - DEM/IST
MECÂNICA DOS FLUIDOS II

Bibliography :
– Sabersky – Fluid Flow: 8.1, 8.2
– White – Fluid Mechanics: 7.1, 7.3, 7.5
2004
Mecânica dos Fluidos II
Prof. António Sarmento - DEM/IST