João Baptista Bayão Ribeiro
USO DO SCILAB PARA REALIZAÇÃO
EM COMPUTADOR DE UM PROJETO
DE UM COMPENSADOR DE ATRASO-AVANÇO
EXEMPLO 7.04 DO OGATA
Rio de Janeiro
2014
2
ÍNDICE
USO DO SCILAB PARA REALIZAÇÃO..........................................................................................1
EM COMPUTADOR DE UM PROJETO............................................................................................1
DE UM COMPENSADOR DE ATRASO-AVANÇO..........................................................................1
SUMÁRIO.......................................................................................................................................3
REQUISITOS DO PROJETO.........................................................................................................4
LISTAGEM 7.4................................................................................................................................7
RESULTADOS..............................................................................................................................10
Outras Saidas da Listagem 7.4..................................................................................................12
3
USO DO SCILAB PARA REALIZAÇÃO
EM COMPUTADOR DE UM PROJETO
DE UM COMPENSADOR DE ATRASO-AVANÇO
EXEMPLO-7.04 DO OGATA
SUMÁRIO
Este documento apresenta um programa escrito para o Scilab que executa em
computador um projeto de um compensador de atraso-avanço segundo o método
preconizado por Ogata, no exemplo 704 do livro Engenharia de Controle Moderno –
3ª Edição.
O raciocínio do procedimento é justificado através da noção do Lugar das Raízes
(LR), que fornece uma noção muito intuitiva sobre os procedimentos utilizados.
A listagem Exemplo7_4 resolve computacionalmente o problema, utilizando o
software Scilab. A idéia é que todos os passos do projeto sejam realizados pelo
computador, não apenas o traçado das curvas de resposta ao degrau e rampa.
4
REQUISITOS DO PROJETO
A Figura 1 apresenta um sistema com realimentação não compensado, onde um
compensador analógico no caminho direto será empregado para satisfazer certos
requisitos de projeto, conforme a metodologia empregada pelo Ogata no Cap.7 do livro
Engenharia de Controle Moderno – 3 ª Edição, baseada no Lugar das Raizes (LR).
O sistema compensado está representado na Figura 2. O caminho de
realimentação, que está representado pelo sensor H(s), será suposto com realimentação
unitária. Portanto neste documento, H(s)=1.
Deseja-se modificar melhorar característica de resposta transiente, ao mesmo
tempo melhorar as características em estado estacionário. Isto significa que o sistema
compensado deve ser mais rápido do que o sistema não compensado, melhorando
também a resposta em estado estacionário.
O Quadro 1 abaixo apresenta como exemplo 10 conjuntos de valores que podem
ser usados como exemplos de entradas na Listagem 7.4. Outros valores, podem ser
empregados, desde que se adequem às condições para as quais o programa foi
idealizado.
Entra
da
G(s)
1
G=10/(s*(s+.5))
2
Quadro 1
zd
wnd
kd
C1=C2
T2
R5
.2
5
80
.0001
5
20000
G=.5/(s*(s+.5))
.5
5
80
.0001
5
20000
3
G=.15/(s*(s+.4))
.8
5
80
.0001
5
20000
4
G=0.44/(s*(s+.6))
.7
5
80
.0001
15
20000
5
G=0.55/(s*(s+.7))
.9
7
60
.0001
15
20000
6
G=0.44/(s*(s+1))
.95
10
90
.0001
10
20000
7
G=1/(s*(s+1.5))
.7
8
40
.0001
10
20000
8
G=.1/(s*(s+.015))
.4
1
100
.0001
6
20000
9
G=.8/(s*(s+.8))
.8
4
60
.0001
8
20000
10
G=8/(s*(s+2.8))
zd: fator de amortecimento desejado
wnd: frequência natural desejada
kd: constante de erro desejada
.6
10
60
.0001
8
20000
5
z_av:valor escolhido do zero do compensador de avanco
T2: Parâmetro do compensador de atraso
C1 e C2 em Farads
R3 em ohms
O zero da parte de avanço do compensador deverá compensar o polo real da planta
Figura 1
Figura 2
O programa possibilita o ajuste de vários parâmetros: a função de transferência do
sistema não compensado, G(s), a frequência natural desejada, o fator de amortecimento
desejado, o valor desejado de constante estática de erro desejado, valores de
parâmetros de circuitos(resistores, capacitores).
Conforme a metodologia estabelecida pelo Ogata no Exemplo 7.4, vemos que a
condição de módulo do LR pode ser expressa como
(mod comp av)(mod comp at)(modulo G(s))Kc=1 para s=polo dominante desejado.
Como
(mod comp at)=1, temos que (mod comp av)=1/Kc(mod G(s)).
Assim, podemos definir k3 como
Kc(mod G(s)) para s=polo dominante, e
utilizá-lo como referência para a relação PB/PA (ver exemplo 7.4 do Ogata - 4ª edição).
Uma vez calculado k3 (linha 46 da listagem) e o angulo de avanço fi necessário, o
polo e o zero do compensador de avanço são obtidos através de um algorítimo ('polo e
zero do compensador de avanço') que, a partir do polo dominante, define um angulo de
giro variável (ang), e para cada valor de ang calcula, para uma abertura fi, os
comprimentos correspondentes aos lados PB e PA do triangulo PAB (ver figura 7.23 do
6
Ogata - 4ª edição).
A seguir, através de um processo que determina o valor minimo da variação
delta1=abs(PB/PA-k3)(PB/PA)=k2 na listagem - esta definiçao de delta1 foi adotada
porque condições extremas de rotação podem levar a valores falsamente negativos para
k2, o que prejudicaria o funcionamento do algoritmo.
Ao verificar a diferença entre valores sucessivos de delta1, pode-se determinar a
ocorrência do mínimo. Os valores significativos ficam guardados no vetor xa. A precisão
do algoritmo pode ser ajustada pelo passo de variação de ang.
7
LISTAGEM 7.4
Baixar a listagem EXEMPLO 4.sce
8
RESULTADOS
Figura 3
Figura 4
As Figura 3 e 4 apresentam o resultado da simulação, gerado pelo programa.
A curva em verde corresponde à saida do sistema não compensado, e a curva em
azul à saida do sistema compensado. Na Figura 4, a curva em vermelho significa o valor
desejado, isto é, a entrada de controle.
9
Observe que o sistema compensado apresenta uma resposta transiente para
resposta ao degrau bem melhor à do sistema não compensado.
A resposta à rampa apresenta erro em estado estacionário sensivelmente menor.
A conclusão é que o sistema compensado pode atender ao objetivo de projeto.
Estas Figuras 3 e 4 foram obtidas pela Listagem 7.4 acima, usando-se os valores
para o sistema não compensado constantes do Ogata no Cap.7 do livro Engenharia de
Controle Moderno – 3 ª Edição – Exemplo7.4.
10
Outras Saidas da Listagem 7.4
Para efeito de validação do valores encontrados, comparamos com os valores
constante do Exemplo 7.4 do Ogata (Engenharia de Controle Moderno – 3ª ou 4ª Edição).
Nota-se que o Ogata usou um método gráfico
para cálculo dos valores, o que
fatalmente leva a aproximações piores do que as obtidas no cálculo numérico via
computador.
1-Função de transferência no caminho direto sistema não compensado
4
G = --------2
0.5s + s
Ogata:
4
G = ---------2
0.5s + s
2-Função de transferência de enlace fechado do sistema não compensado
4
T T = --------------------2
4 + 0.5s + s
Ogata:
4
T T = --------------------2
4 + 0.5s + s
3-Polos do sistema não compensado
p_nc =
column 1
- 0.25 - 1.9843135i
column 2
- 0.25 + 1.9843135i
Ogata: Não calculado
11
4-Frequência natural , fator de amortecimento e sobre-sinal máximo do sistema não
compensado
wn = 2.
zeta = 0.125
Mp = 0.6731390 (Mp significa máximo sobre-sinal)
Ogata:
wn = 2.
zeta = 0.125
5-Constante de erro do sistema não compensado
kv = 8.
Ogata:
kv = 8.
6-Fator de amortecimento desejado (valor de projeto)
zetad=0.5
Ogata:
zetad=0.5
7-Frequência natural não amortecida desejada (valor de projeto)
wnd=5
Ogata:
wnd=5
8-Constante de erro desejada (valor de projeto)
kvd=80
Ogata:
kvd=80
9-Polos dominantes desejados
polos_dom =
column 1
- 2.5 + 4.330127i
column 2
- 2.5 - 4.330127i
12
Ogata:
polos_dom =
column 1
- 2.5 + 4.33i
column 2
- 2.5 - 4.33i
10-Ganho do compensador
Kc = 10.
Ogata:
Kc = 10.
11-Relação PB/PA do compensador de avanço
k3
=1.6772557
Ogata:
k3
=1.6772557
12-Ângulo do lugar geométrico dos pontos no plano s com fator de amortecimento zetad (reta
radial).
teta = 60.
13-Ângulo de avanço necessário (em graus)
fi
= 54.791281
Ogata:
fi
= 55
14-Polo e zero do compensador de avanço
z_av =- 2.3946769
p_av =- 8.3300813
Ogata:
z_av = - 2.38
p_av = - 8.34
15-Parâmetros do compensador de avanço
T1 = 0.4175929
13
beta = 3.4785825
Ogata:
T1 = 0.420
beta =3.503
16-Função de transferência enlace aberto parcial'
Gp
9.5787076 + 4s
-------------------------2
3
4.1650406s + 8.8300813s + s
=
17-Parâmetros do compensador de atraso
T2 = 10.
Ogata:
T2 = 10.
18- Polo e zero do compensador de atraso
p_at =- 0.0287473
z_at =- 0.1
Ogata:
p_at = - 0.0285
z_at =- 0.1
19-Função de transferência do compensador atraso-avanco
2
2.3946769 + 24.946769s + 10s
Gc= ------------------------------------------------2
0.2394677 + 8.3588286s + s
20-Função de transferência de enlace aberto do sistema compensado
Gea=
2
9.5787076 + 99.787076s + 40s
-------------------------------------2
3
4
0.1197338s + 4.418882s+ 8.8588286s + s
14
21-Polos da fea do sistema compensado
polosfea
=
- 8.3300813
- 0.5
- 0.0287473
0
Ogata:
polosfea
=
- 8.34
- 0.5
- 0.0285
0
22-Zeros da fea do sistema compensado
zerosfea =
- 2.3946769
- 0.1
Ogata:
zerosfea =
- 2.38
- 0.1
23-Função de transferência de enlace fechado do sistema compensado
2
9.5787076 + 99.787076s + 40s
Gef =-----------------------------------------------------2
3
4
9.5787076 + 99.90681s + 44.418882s + 8.8588286s + s
24-Polos do sistema compensado
polos =
- 2.4381455 + 4.3203114i
- 2.4381455 - 4.3203114i
- 3.8822806
- 0.1002570
Ogata:
polos =
-
2.4539+ 4.30994i
2.4539 - 4.3099i
3.8604
0.1
15
25-Zeros do sistema compensado
zeros =
- 2.3946769
- 0.1000000
Ogata:
zeros =
- 2.4
- 0.1
26-Polos dominantes do sistema compensado
p_d_1 = - 2.4381455 + 4.3203114i
p_d_2 = - 2.4381455 - 4.3203114i
Ogata:
p_d_1 = - 2.4539+ 4.30994i
p_d_2 = - 2.4539-4.30994i
27-Frequência natural e fator de amortecimento do sistema compensado
sistema não compensado
wnc = 4.9608108
zetac = 0.4914813
wn = 2.
zeta = 0.125
Objetivos de projeto
wnd =5
zetad = 0.5
Ogata:
wnc=4.9595
zetac=0.4956
28-Constante de erro do sistema compensado
kvc=80.
Sistema não compensado: kv=8
Objetivo de projeto:
kvd=80
16
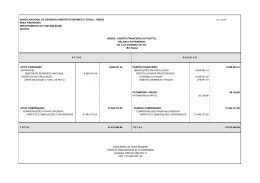
29-Projeto eletrônico
C1 = 0.0001
C2 = 0.0001
R1 =1200.4685
R2 =100000.
R3 = 2975.4602
R4 =247858.25
R5 =20000.
R6 = 80691.281
Figura 5
Como o polo a malha fechada do sistema compensado localizado em - 0.1002570
está muito próximo do zero em -0.1, praticamente se cancelam. O polo do sistema
compensado em - 3.8822806 não se cancela com o zero em - 2.3946769 . O
efeito resultante é um reforço na sobretensão da resposta ao degrau.