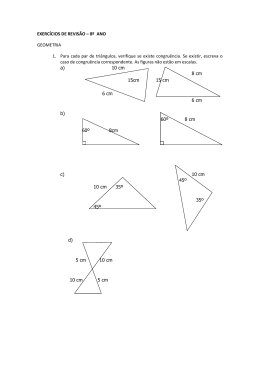
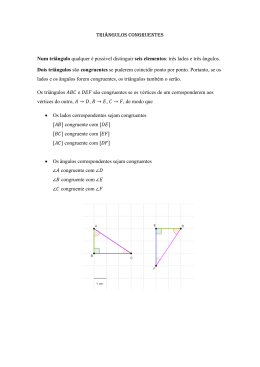
Pré-vestibular – Matemática
Caderno 1 – Unidade IV – Série 3
Resoluções
Segmento: Pré-vestibular
Coleção: Alfa, Beta e Gama
Disciplina: Matemática
Volume: 1
Unidade IV: Série 3
Congruência de triângulos
1. Queremos mostrar que os ângulos da base de um triângulo isósceles são
congruentes.
Temos que:
• AB = AC
• CA = BA
• BC = CB
Logo, os triângulos ΔABC e ΔACB são congruentes, pelo caso LLL. Como
consequência ABC = ACB.
(c.q.d.)
2. Queremos mostrar que o segmento que une o vértice A ao ponto médio M da
base BC , de um triângulo isósceles, é a bissetriz do ângulo A .
Temos que:
• AB = AC
• BM = CM
• AM = AM
Logo, pelo caso LLL os triângulos ∆ABM e ∆ACM são congruentes. Assim,
BAM = CAM , ou seja, AM é a bissetriz do ângulo A .
(c.q.d.)
1
Pré-vestibular – Matemática
Caderno 1 – Unidade IV – Série 3
3. Observando a figura, temos que:
• DC = BA
• CA = AC
• DA = BC
Logo, pelo caso LLL, os triângulos I e II são congruentes. Com isso, tem-se:
DCA = BAC ⇒ e = a

CAD = ACB ⇒ f = c
 ADC = CBA ⇒ d = b

a) F
b) F
c) F
d) V
e) F
f) V
4. Queremos provar que PR = PS.
Observando a figura, temos que:
• PRA = PSA
• RAP = SAP
• AP = AP
Pelo caso LAA os triângulos ∆RAP e ∆SAP são congruentes. Logo, RP = SP.
(c.q.d.)
5. Temos que:
• OA = OB (raio)
• AM = BM (por construção)
• OM = OM
Pelo caso LLL os triângulos ∆AMO e ∆BMO são congruentes. Logo:
(I): AMO = BMO
Sabemos que (II): AMO + BMO = 180°, então de (I) e (II), temos:
BMO + BMO = 180° ⇒ α + α = 90°
(c.q.d.)
2
Pré-vestibular – Matemática
Caderno 1 – Unidade IV – Série 3
ɵ = ECB . Como BE e CD são bissetrizes, temos
6. Do enunciado, temos que DBC
ɵ = EBD
ɵ . Atentemo-nos as seguintes igualdades:
que: DCE = BCD = CBE
ɵ = ECB
• DBC
• BC = CB
ɵ
• BCD = CBE
Logo, pelo caso ALA, os triângulos ∆BCD e ∆CBE são congruentes.
(c.q.d.)
7. Temos que:
• OT = OS (raio)
• OP = OP
• OTP = OSP = 90°
Pelo caso especial HP (hipotenusa-cateto), os triângulos ∆OTP e ∆OSP são
congruentes.
ɵ = OPT
ɵ , ou seja, O se encontra na bissetriz do ângulo θ .
Com isso, OPS
(c.q.d.)
8. Temos que:
• AM = BM (por construção)
• CMA = DMB (o.p.v)
• ACM = BDM (hipótese)
Assim, pelo caso LAA os triângulos ∆ACM e ∆BDM são congruentes.
Logo AC = BD.
(c.q.d.)
9. Como AD = BE e AB = BC, podemos afirmar que AB – AD = BC – BE, ou seja,
DB = EC. Assim, temos:
• DB = EC (provado)
ɵ = ECF (hipótese)
• DBE
• BE = CF (hipótese)
Logo, pelo caso LAL os triângulos ∆DBE e ∆ECF são congruentes e, portanto:
DE = EF.
De modo análogo, temos que:
• EC = FA
• ECF = FAD
• CF = AD
Logo, pelo caso LAL os triângulos ∆ECF e ∆FAD são congruentes e, portanto:
EF = FD.
Assim DE = EF = FD, ou seja, DEF é equilátero.
(c.q.d.)
3
Pré-vestibular – Matemática
Caderno 1 – Unidade IV – Série 3
10. A
Temos que:
• AP = BP (hipótese)
ɵ = BPQ
ɵ = 90°
• APO
• PO = PO
Pelo caso especial HC (hipotenusa-cateto), os triângulos ∆APO e ∆BPO são
congruentes. Logo AOP = BOP (I)
De maneira análoga, temos que:
• BQ = CQ (hipótese)
• BQO = CQO = 90°
• QO = QO
Pelo caso especial HC (hipotenusa-cateto), os triângulos ∆BQO e ∆CQO são
congruentes. Logo: BOQ = COQ = 90° (II)
Sabemos que BOP = BOQ = θ (III).
Substituindo (I) e (II), temos:
AOC = AOP + BOP + BOQ + COQ
= BOP + BOP + BOQ + BOQ
= 2( BOP + BOQ )
Substituindo (III):
2( BOP + BOQ ) = 2 θ
4