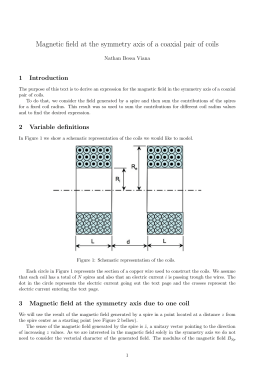
Surfaces of revolution with constant curvatures in cylindric-conformally
flat 3-spaces
Kellcio O. Araújo, Armando V. Corro, Romildo Pina and Marcelo Souza
∗
June 14, 2013
Abstract
In this work, we study curvatures of surfaces of revolution with respect to the cylindrical metrics that are conformal to the
Euclidean metric. We introduce the Riemannian manifold E3F which is the Euclidean space R3 endowed with a conformally flat
metric < , >g with the conformal factor 1/F 2 , where F (x1 , x2 , x3 ) = F (r), r = x21 + x22 , and F : R → R, is a differentiable
function, we will call them cylindric-conformally flat 3-spaces. Here we consider only surfaces of revolutions around the x3 -axis.
We characterize surfaces of revolution with constant Gaussian curvature in E3F . We show that all the cylinders with x3 −axis are
√
flat surfaces for all F , and if F (r) = r, we prove that the space E3√r is a complete manifold, and all the surfaces of revolution
are flat surfaces in E3√r .
We characterize surfaces of revolution with constant extrinsic curvature. Besides, we prove that all the planes perpendicular
to the x3 −axis have null extrinsic curvature for all F and we show that any cylinder has constant extrinsic curvature. If
√
F (r) = r then all the surfaces of revolution have null extrinsic curvature. We also prove that if F (r) = √1r , unless the planes
perpendicular to the x3 −axis the unique surfaces of revolution with zero extrinsic curvature are the catenoids with x3 −axis.
√
Furthermore, we exhibit two complete spaces, for F (r) = e−r and F (r) = r + 1, for which all the cylinders with x3 −axis have
positive and negative constant extrinsic curvature, respectively.
1
Introduction
It is well known that only the cylinder and the plane are complete flat surfaces in the Euclidean space R3 . The study of
flat surfaces is a very interesting topic in Differential Geometry. The authors in [2] proved the existence of complete surfaces
of rotation with non positive constant extrinsic curvature in a conformally flat 3-space. The authors in [2] studied surfaces
of rotation with constant extrinsic curvature in (R3 , < , >g1 ) whose the components of the metric < , >g1 are given by
g1 := (gij ) =
1
δ ,
F 2 ij
2
2
2
where F (x) = e−x1 −x2 −x3 , x = (x1 , x2 , x3 ) ∈ R3 . This particular metric appears as a solution to the
Einstein equation obtained by Pina and Tenenblat [4], with a great potential of applications in physics. In [3] the authors
studied rotational surfaces in (R3 , < , >g ), where the conformal factor of the metric is invariant on each sphere and showed
that the round sphere of radius R, centered at origin, has constant extrinsic curvature. Also, they show that the radial lines
are geodesics in their space. They proved that the round spheres centered at origin have zero extrinsic curvature if and only if
√
the conformal factor 1/F 2 is given by F (t) = λ t, 0 6= λ = constant, t := x21 + x22 + x33 . In this special case, they proved that
√
the space (R3 \ {0}, < , >g ), where F (t) = t, is a complete manifold with non negative sectional curvature, and any round
sphere of radius R, centered at origin, is a compact minimal surface and has constant Gaussian curvature K = 1.
∗ 2000
Mathematics Subject Classification: 53C21, 53C42. The authors were partially supported by CAPES/PROCAD-NF. E-mail
addresses: [email protected], [email protected], [email protected], [email protected]
1
2
The conformally flat 3-spaces with cylindrical metrics
We consider (R3 , < , >) which is the 3-dimensional real vector space R3 endowed with the canonical Euclidean metric denoted
by < , >. Now, let us consider a metric < , >g that is conformal to the Euclidean metric < , >. Similarly, we denote by
(R3 , < , >g ) the Euclidean space R3 endowed with the metric < , >g .
In this section, we study a conformally flat 3-space (R3 , < , >g ), where the metric < , >g is any metric which is conformal
to the Euclidean metric < , > such that its conformal factor 1/F 2 is invariant on a cylinder Cr of radius r, for each r.
In the next result we study geodesics in E3F .
Theorem 2.1. Consider the Riemannian manifold E3F . Then,
a) The straight lines perpendicular to the x3 −axis are geodesics in E3F , ∀F .
b) circles centered and ortogonal to the x3 −axis are geodesics in E3F if and only if F (r) =
√
r;
√
c) if F (r) = r the straight lines orthogonal to the x3 -axis that are geodesics in E3F , are only the perpendicular ones;
Now, we choose F (r) =
√
r and we considered the space R3 \ {x3 − axis} endowed with the same metric of E3F .
Theorem 2.2. Let R3√r = R3 \ {x3 − axis} be the space endowed with the metric < , >g , where g := (gij ) = (δij )/[F (r)]2 , and
√
F (r) = r. Then, R3√r is complete and it has non positive sectional curvature given by
K
2.1
∂
∂
,
∂x1 ∂x2
= 0, and K
∂
∂
,
∂xα ∂x3
x2α
=−
(x21
3
+ x22 ) 2
, 1 ≤ α ≤ 2.
Flat surfaces of revolution
We note that set of rotations around the x3 -axis are isometries of E3F . The following result characterizes all the surfaces of
revolution X with constant Gaussian curvature in E3F .
Theorem 2.3. Let S be a surface of revolution in E3F .
a) All the cylinders with x3 −axis are flat surfaces, for all F ;
b) If F (r) =
2.2
√
r, then unless the planes perpendicular to the x3 −axis, all the surfaces of revolution S are flat surfaces.
Surfaces of revolution with constant extrinsic curvature
In this section, we study surfaces of revolution with constant extrinsic curvature. We obtain examples of complete and non
complete conformally flat manifolds.
Theorem 2.4. Let S be a surface of revolution in E3F :
a) planes perpendicular to the x3 −axis have zero extrinsic curvature for all F ;
b)If F (r) =
√
r then, all the surfaces of revolution S have zero extrinsic curvature;
c) If F (r) =
√1 ,
r
then, unless the planes perpendicular to the x3 −axis, the unique surfaces of revolution with zero extrinsic
curvature are the catenoids with x3 −axis.
2
In the next result, we obtain
Theorem 2.5. Consider the conformally flat space E3F .
a) Then, for all F the cylinder of radius R and x3 -axis has constant extrinsic curvature given by
K̃E = 2Ḟ (R2 ) −F (R2 ) + 2R2 Ḟ (R2 )
(1)
b) If F (r) = e−r , then the space E3F is a complete manifold. Besides, the cylinder of radius R with x3 −axis has positive
constant extrinsic curvature given by
K̃E =
c) If we consider the function F (r) =
√
2(1 + 2R2 )
.
e2R2
(2)
r + 1. Then, E3F is a complete manifold and the cylinder with x3 −axis and radius R
1
has negative constant extrinsic curvature given by K̃E = − R
.
References
[1] Corro, A. V. - Generalized Weingarten surfaces of Bryant type in hyperbolic 3- space. Mat. Contemp., 30, (2006) 71-89.
[2] Corro, A. V.; Pina, R. S.; Souza, M. A. - Surfaces of Rotation with constant extrinsic curvature in a conformally flat
3-space. Results in Mathematics, 60 (2011), 225-234.
[3] Corro, A. V.; Pina, R. S.; Souza, M. A. - Spheres in a conformally flat 3-space, preprint.
[4] Pina, R. S.; Tenenblat, K. - On solutions of the Ricci curvature equation and the Einstein equation. Israel Journal of
Mathematics, 171 (2009), no. 1, 61-76.
Kellcio O. Araújo
Departamento de Matemática
Universidade de Brası́lia - UnB
70910-900, Brası́lia, DF, Brazil
E-mail: [email protected]
Armando V. Corro
Instituto de Matemática e Estatı́stica
Universidade Federal de Goiás - UFG
74001-970, Goiânia, GO, Brazil
E-mail: [email protected]
Romildo Pina
Instituto de Matemática e Estatı́stica
Universidade Federal de Goiás - UFG
74001-970, Goiânia, GO, Brazil
E-mail: [email protected]
Marcelo Souza
Instituto de Matemática e Estatı́stica
Universidade Federal de Goiás - UFG
74001-970, Goiânia, GO, Brazil
E-mail: [email protected]
3