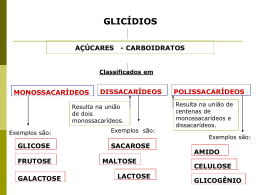
Uma piscina como modelo para ajudar a compreender as técnicas que usam
compostos marcados para estudar o metabolismo
1- Cálculo da velocidade com que a água entra numa piscina sabendo a quantidade de lixívia que se
tem de adicionar para manter a concentração de lixívia constante
Imaginemos uma piscina com dimensões desconhecidas alimentada por uma fonte que se situa algures no
fundo da piscina (uma fonte subaquática). Admitamos ainda que a quantidade total de água na piscina é
constante porque a velocidade de entrada de água na piscina é igual à velocidade com que esta se escapa para
um esgoto. Se chamarmos Ra (Rate of appearance) à velocidade de entrada de água na piscina e Rd (Rate of
desappearance) à velocidade de saída de água no esgoto teremos de concluir que Ra=Rd.
Admitamos que a água da piscina já contém cloro e que, para manter a piscina “clorada” é importante que
a concentração de lixívia na água da piscina seja constante; admitamos que esta concentração é de facto
constante e que é de 2 gotas de lixívia/L de água. Chamemos a esta concentração “enriquecimento” e usemos
a sigla E para expressar o seu valor. O objetivo é, portanto, manter E constante, mas se se parar de adicionar
lixívia à piscina, E vai obrigatoriamente diminuir porque a água que sai para o esgoto é água “clorada”
enquanto a que entra não o é.
Se se soubesse que a velocidade de entrada de água na piscina (água não “clorada”, obviamente) era, por
exemplo, de 10 L/minuto (Ra = 10 L min-1) era imediato concluir que a velocidade de adição de lixívia
deveria ser de 20 gotas/min. Se chamarmos F à velocidade de adição de lixívia, a Equação 1 permite
relacionar o seu valor com a concentração de lixívia na água da piscina (E) e com a velocidade de entrada de
água não “clorada” na piscina (Ra).
Equação 1
F = E × Ra ⇔ Ra =
F
E
Admitamos que não se sabia a velocidade de entrada de água (Ra era desconhecido) mas que, por
tentativa e erro, se tinha concluído que, adicionando 20 gotas de lixívia/min (F= 20 gotas min-1), E se
mantinha constante e igual a 2 gotas/L. Nesse caso, podia-se usar a Equação 1 para calcular Ra e concluir
que o seu valor era de 10 L min-1. Se se consegue manter a concentração estabilizada no valor de 2 gotas L-1
continuando a adicionar 20 gotas min-1 teríamos de concluir que Ra tinha sido, no intervalo de tempo
considerado, de 10 L min-1.
2- Cálculo da velocidade com que uma substância que se forma endogenamente (ou é absorvida no
intestino) e entra no líquido extracelular usando tracers, admitindo enriquecimento constante
A glicose está continuamente a ser produzida no fígado (e, em menor grau, no rim) e a passar deste órgão
para o plasma sanguíneo e, de seguida, para o restante líquido extracelular. Porque, na ausência de ingestão
de glicose, a concentração de glicose no plasma sanguíneo se mantém, em condições “normais”,
praticamente constante é imediato concluir que, nestas condições, as velocidades de produção (Ra) e de
utilização de glicose pelas células do organismo (Rd) são também praticamente iguais mas, sem outros
dados, não podemos concluir mais nada acerca dos seus valores. Quando a concentração plasmática de
glicose desce, isso pode ser causado por diminuição da velocidade da entrada de glicose para o plasma
(diminuição de Ra), a aumento da velocidade de captação pelas células (aumento de Rd) ou a ambos. Da
mesma forma, se a concentração de glicose no plasma sanguíneo sobe a seguir a uma refeição que contém
glicose ou a substância que a possam originar (amido, por exemplo) é de concluir que Ra > Rd, mas também
não podemos concluir nada acerca dos seus valores.
A determinação de Ra (e de Rd) exige estudos em que se usa glicose marcada.1 Esta marcação pode fazerse substituindo um ou mais átomos de carbono 12 por átomos de carbono 14 (o 12C e o 14C são isótopos do
carbono) ou um ou mais átomos de hidrogénio por deutério ou trítio (também isótopos do hidrogénio). Se,
por exemplo, se usar glicose em que o hidrogénio ligado ao carbono 3 é marcado (trítio em vez do
hidrogénio, por exemplo) ou átomos de deutério ligados ao carbono 6, os valores de Ra e Rd podem ser
determinados. As moléculas de glicose que entram nas células são metabolizadas nessas células e, em
1
Nestas técnicas usa-se a palavra tracer para designar a substância marcada (glicose marcada no caso) e tracee para
designar a mesma substância independentemente de estar ou não marcada.
Página 1 de 4
determinados passos desse metabolismo (ação da isomérase das trioses fosfato e via das pentoses), o
hidrogénio ligado ao carbono 3 passa para a água e deixa de estar ligado aos intermediários do metabolismo
da glicose. No caso de a marcação ter sido feita com átomos de deutério no carbono 6, os passos do
metabolismo em que o deutério passa para a água situam-se mais distalmente (na ação da carboxílase do
piruvato e da fumárase), mas a consequência relevante é a mesma: os intermediários do metabolismo gerados
depois da ação destas enzimas deixam de conter deutério. Mesmo que esses intermediários possam gerar
outra vez glicose no fígado, a glicose que aí é produzida já não contém marcação. Ou seja, se um indivíduo
tiver, num dado momento, glicose marcada no plasma sanguíneo, à medida que o fígado vai produzindo
glicose não marcada, a proporção de moléculas de glicose marcada tende a diminuir no sangue. A proporção
de moléculas marcadas também diminui se a glicose estiver a entrar no organismo, não apenas porque está a
ser produzida no fígado (produção endógena)2, mas porque está também a ser absorvida no intestino (entrada
exógena).
A proporção em análise, designa-se por enriquecimento (E) e, quando E diminui, isso significa que as
moléculas de glicose marcada estão a ficar “diluídas” por haver aumento da proporção das moléculas de
glicose não marcada. É por isso que este tipo de técnicas são designadas por “ técnicas de diluição isotópica”
embora, de facto, se baseiem na velocidade com que se deve administrar a substância marcada para
contrariar o aumento de “diluição”. E é uma medida do número de moléculas de glicose marcadas
relativamente à quantidade de glicose total e, se se usar glicose radiativa, pode ser expressa em nCi/mg de
glicose, por exemplo3.
Quando se administra glicose marcada, porque a glicose que está no cateter tem um grau de
enriquecimento muito elevado é frequentemente possível administrar quantidades mínimas de glicose e, sem
grande erro, desprezar a massa de glicose administrada.4 Admitamos que, após a administração de um “bolo
de glicose marcada”, o valor do enriquecimento da glicose no sangue se manteve constante e igual a 2,2
nCi/mg de glicose (E) durante 1h. Admitamos também que essa constância só foi possível porque, de forma
contínua, se foi administrando glicose marcada à velocidade de 300 nCi/min. Seria este o valor de F, a
velocidade de infusão da glicose marcada. Usando a Equação 1, é possível concluir que a velocidade com
que, nesse intervalo de tempo, a glicose estrou no plasma foi de 136 mg/min (Ra). Ver Equação 2.
Equação 2
Ra =
F
300 nCi min -1
⇒ 136 mg min -1 =
2,2 nCi mg -1
E
3- Cálculo da velocidade com que uma determinada substância está a ser utilizada pelas células (Rd)
Se, no intervalo de tempo considerado no Capítulo anterior (1 hora) e independente do valor original, a
concentração de glicose no plasma sanguíneo se tiver mantido também constante é de concluir que a
velocidade com que foi utilizada pelos tecidos (Rd) foi também de 136 mg/min. (Estamos obviamente a
presumir que o volume do líquido extracelular, plasma incluído, não variou e que por isso a massa total de
glicose neste “compartimento” do organismo também se manteve constante.)
Se a concentração de glicose no plasma sanguíneo subiu (glicose química, medida por exemplo, em
mg/dL) será de admitir que a velocidade de utilização da glicose pelas células (Rd) foi inferir à velocidade
com que está a entrar no “compartimento” extracelular (Ra). Rd<Ra mas, para calcular a diferença entre
estes dois valores a partir da variação de concentração teremos que saber o volume do líquido extracelular
total (plasma incluído). Se a concentração tiver passado de, por exemplo, 80 para 89,6 mg/dL (diferença de
9,6 mg/dL) e admitirmos que o volume extracelular é de 10 L, o incremento da massa de glicose neste
compartimento foi de 960 mg. No intervalo de tempo considerado, a velocidade média da variação da
quantidade de glicose no compartimento extracelular foi de 16 mg/min (960 mg/60 min).
Nessas condições, Rd<Ra e a diferença foi de 16 mg/min. Dado que Ra era de 136 mg/min, é de concluir
que a velocidade Rd (velocidade de armazenamento como glicogénio e catabolismo) foi de 120 mg/min.
2
A produção endógena hepática de glicose, no sentido que lhe estamos a dar (não o balanço entre a entrada e a saída de
moléculas de glicose no fígado, mas a saída de moléculas de glicose do fígado) raramente se anula.
3
O nCi é uma medida de radiatividade.
4
Isto não é completamente verdade se a marcação tiver sido feita com deutério que não é radioativo e exige o uso de
técnicas menos sensíveis para a sua determinação. Neste caso há que introduzir correções nos cálculos, mas isto
ultrapassa o objetivo deste texto.
Página 2 de 4
A Equação 3 onde C2 e C1 são as concentrações de glicose no fim e no início do intervalo de tempo em
questão (t2-t1) e V é volume do compartimento extracelular, resume o que se escreveu acima5.
Equação 3
Rd = Ra −
(C2 − C1)
V
(t2 − t1)
4- Calcular a velocidade de entrada de água numa piscina em que a concentração de lixívia variou
Voltando ao modelo da piscina. Acima, admitimos que num intervalo de tempo considerado (entre a hora
0:00 e a hora 1:00, por exemplo) a concentração de lixívia na água da piscina (E) se manteve constante (E= 2
gotas L-1) à custa da adição de 20 gotas de lixívia por minuto (F= 20 gotas min-1) e foi com estes dados que
calculamos que a velocidade de Ra (a entrada de água na piscina) era de 10 L min-1.
Podemos, no entanto, admitir que apesar de a velocidade de adição de lixívia se ter mantido constante, se
notou uma variação na 2ª hora, ou seja, que entre a hora 1:00 e a hora 2:00 o valor de E se modificou.
Imaginemos que baixou, passando de 2 gotas L-1 na hora 1:00 para 1,4 gotas L-1 na hora 2:00. Neste caso
teria de concluir-se que a fonte subaquática debitou mais água nessa segunda hora e que, se quiséssemos
manter E constante, teria de se ter aumentado a velocidade de adição de lixívia; ou seja, teríamos de ter
aumentado o valor de F.
Embora o valor de Ra seja, nestas condições, difícil de calcular com precisão, poderia fazer-se uma
estimativa.
Admitindo que a diminuição no valor de E durante a segunda hora aconteceu de forma gradual, pode
calcular-se que a velocidade de diminuição de E durante a segunda hora foi de 0,01 gotas L-1 min-1.
Equação 4
(E2h-E1h) /60 min; (2 gotas L-1 – 1,4 gotas L-1)/60 min = 0,01 gotas L-1 min-1
Para que a E se mantivesse constante deveria ter-se adicionado não 20 gotas/min, mas sim 20 gotas/min
acrescidas do número de gotas que contrariasse esta diluição da lixívia na água. Ao contrário do que
aconteceria quando E se mantinha constante, neste caso, para sabermos o número de gotas a adicionar a
mais, teríamos de saber o volume da piscina. O número de gotas de lixívia a adicionar seria, neste caso, dado
pela Equação 5.
Equação 5
20 gotas/min + 0,01 gotas L-1 min-1 × L de água na piscina
Se tivéssemos uma ideia do volume da piscina (admitamos que era 10 000 L) poderíamos saber que o
valor a acrescentar às 20 gotas/min deveria ser de 100 gotas/min, ou seja, que deveríamos ter adicionado 120
gotas/min. Neste caso poderíamos estimar Ra durante a segunda hora usando a Equação 1.
No entanto, o uso dessa equação implica conhecer o valor de E e, nesse intervalo de tempo, o valor de E
variou entre 2 gotas L-1 e 1,4 gotas L-1. Uma estimativa do seu valor será a média, ou seja, 1,7 gotas L-1.
Fazendo E = 1,7 gotas L-1 e tendo admitido que 120 gotas min-1 seria o valor de F (chamemos-lhe F’) que
contrariava a diluição da lixívia, poderemos usar a Equação 1 para concluir que Ra foi de 70,6 L min-1 (ver
Equação 6).
Equação 6
Ra =
F'
120 gotas min -1
⇒ 70,6 L min -1 =
E médio no intervalo
1,7 gotas L-1
5- A velocidade com que uma substância entra no espaço extracelular usando tracers, admitindo
variação no enriquecimento
A Equação 1 permite calcular Ra (a velocidade de entrada de glicose no compartimento extracelular) se E
(enriquecimento da glicose) e F (velocidade de infusão de glicose marcada) forem constantes mas, há
semelhança do que foi descrito no Capítulo anterior com o modelo da piscina, se se conhecer (ou estimar) o
volume do compartimento extracelular também é possível estimar o valor de Ra usando a mesma Equação
(ou uma Equação semelhante, a Equação 6). Quando o valor de F que foi escolhido se revelou inadequado
5
É de notar que, aplicando a Equação 3, Rd fica maior que Ra se C2<C1; ou seja, se a concentração de glicose tiver
diminuído é de concluir que, no intervalo de tempo em que ocorreu essa diminuição, Rd>Ra.
Página 3 de 4
para manter E constante, pode estimar-se o valor de F que deveria ter sido usado (F’) e fazendo E igual à
média no intervalo, usar uma variante da Equação 1 (a Equação 6) para calcular Ra.
A analogia da piscina precisa de ser repensada para se adaptar ao caso do aparecimento de glicose no
organismo porque, neste caso, o enriquecimento (E) não se mede em gotas/volume de água mas, no exemplo
em análise, em nCi/mg de glicose.
Se, mantendo a velocidade de infusão do tracer (F) em 300 nCi/min, o enriquecimento (E) tiver, no
intervalo de 1 hora, baixado de 2,2 nCi/mg de glicose para 1 nCi/mg de glicose deveremos concluir que, para
impedir a descida do enriquecimento, F deveria ter sido maior. Admitamos também que a quantidade total de
glicose de glicose no compartimento extracelular era de 10 000 mg (que o volume era de 10 L e que a
concentração média no intervalo era de 100 mg/dL, por exemplo). Teríamos de concluir que para manter E
constante a quantidade de tracer administrado no intervalo de 1 hora deveria ter sido aumentado em 12 000
nCi [=10000 mg × (2,2 nCi/mg-1,0 nCi/mg)]. A velocidade de infusão do tracer não deveria ter sido de 300
nCi/min, mas sim de 300 nCi/min acrescidos de 200 nCi/min (=12 000 nCi/60 min).
A Equação 7 permite calcular o valor de F que seria adequado para manter o valor de E constante no
intervalo de tempo em análise (F’). Nesta equação V é o volume extracelular, (C2+C1)/2 é a concentração
média da glicose no intervalo e E2-E1 a variação do enriquecimento no intervalo em análise (t2-t1)6.
Equação 7
(C2 + C1)
× V × (E2 - E1)
2
F' = F −
(t2 − t1)
Tendo calculado um novo valor para F (F’) já se pode usar a Equação 1 atribuindo a E o valor médio de E
no intervalo.
Equação 8
Ra =
F'
E2 + E1
2
O cálculo de Ra quando E varia é sempre um processo que se tenta evitar porque pressupõe uma
estimativa do volume do compartimento extracelular (plasma incluído) e obriga a admitir que a glicose se
espalha instantaneamente por todo esse compartimento. Porque não é verdade que este processo seja
instantâneo, as estimativas de Ra (e Rd) feitas em condições em que E varia tem erros que podem ser ou não
ser negligenciáveis.
Explicações mais pormenorizadas acerca dos fundamentos dos métodos de diluição isotópica foram
explicadas por Wolff [1].
1.
Wolfe RR (1992) Radiactive and stable isotope tracers in biomedicine. Principles and
practice of kinetic analysis. Wiley-Liss, New York.
6
É de notar que, aplicando a Equação 7, F’ fica maior que F se E2<E1, ou seja, se o enriquecimento tiver diminuído
dever-se-ia ter utilizado uma velocidade de infusão do tracer maior (F’>F).
Página 4 de 4