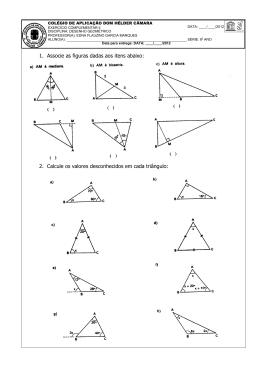
resolução de atividades Capítulo 2 Módulo 1: Reta, semirreta e segmento de reta Página 44 Atividades para classe 1 A figura a seguir mostra um cubo e as retas suportes de algumas arestas. Indique em seu caderno os pares de retas paralelas, os pares de retas concorrentes e os pares de retas reversas. b a b) Construa uma reta, concorrente à reta r, que passe por A. Resposta possível. B r A s c) Construa uma reta, paralela à reta r, que passe por B. Resposta possível. t B r c d Paralelas: (b, c); (b, d); (c, d); concorrentes: (a, b); reversas: (a, c); (a, d). 2 As afirmações abaixo têm erros de conceito. Explique em seu caderno por que essas afirmações são falsas. a) Duas retas que não têm ponto em comum são reversas. Duas retas que não têm ponto em comum podem ser reversas ou paralelas. b) Duas retas que têm um ponto em comum são concorrentes. Duas retas que têm um ponto em comum podem ser concorrentes ou coincidentes. Duas retas que têm apenas um ponto em comum são concorrentes. c) Duas retas coplanares são paralelas. Duas retas coplanares podem ser coincidentes, concorrentes ou paralelas. d) Duas retas reversas podem ser coplanares. Duas retas reversas nunca são coplanares. e) Duas retas coplanares são concorrentes. Duas retas coplanares podem ser coincidentes, concorrentes ou paralelas. 3 Desenhe uma reta ela, ___ r em seu caderno e, sobre___ um segmento CD congruente ao segmento AB a seguir. B 5 Sabendo que ___na figura a seguir B é ponto médio do segmento AC, e que AC 5 8 cm e BD 5 9 cm, determine ___ em seu caderno a medida dos segmentos ___ AB e CD . A C D 4 Faça o que se pede nos itens a seguir. a) Construa uma reta r. Marque um ponto A sobre r e um ponto B fora de r. Resposta possível. B r A C D 6 Em seu caderno, determine o valor de x em cada caso. x a) 32 A 15 C B x 5 AB 5 AC 1 CB. Assim, x 5 32 1 15 V x 5 47 42 b) 26 A C x C x B AB 5 AC 1 CB. Assim, x 1 26 5 42 V x 5 42 2 26 V V x 5 16 c) 23 2x 1 5 B AB 5 AC 1 CB. Assim, (2x 1 5) 1 x 5 23 V V 2x 1 5 1 x 5 23 V 3x 1 5 5 23 V 3x 5 23 2 5 V 18 V 3x 5 18 V x 5 ___ 5 6 3 O segmento CD deve ter a mesma medida do seg___ mento AB . r B • AB 1 BC 5 AC. Se o ponto B é o ponto médio do ___ segmento AC , então ___AB 5 BC. Como o segmento AC mede 8 cm, tem-se AB 1 BC 5 5 8 V 2AB 5 8 V AB 5 BC 5 4 cm. ___ • ___ BC 1 CD 5 BD. Como o segmento BD mede 9 cm e BC mede 4 cm, tem-se 4 1 CD 5 9 V CD 5 5 cm. 3x 2 3 d) ___ s d)Qual é a posição relativa entre as retas traçadas nos itens b) e c)? São retas concorrentes. A A A A 2x 2 2 7 C B AB 5 AC 1 CB. Assim, (2x 2 2) 1 7 5 3x 2 3 V V 2x 2 2 1 7 5 3x 2 3 V 2x 2 3x 5 2 3 1 2 2 7 V V 2x 5 28 V x 5 8 2x 1 1 e) A 6 C 9 B AB 5 AC 1 CB. Assim, 2x 1 1 5 6 1 9 V 2x 5 14 5 6 1 9 2 1 V 2x 5 14 V x 5 ___ 5 7 2 38 4P_YY_M8_RA_C02_038a067.indd 38 29.10.08 14:38:49 resolução de atividades Capítulo 2 7 Determine em seu caderno o valor de x em cada um dos casos ___ a seguir, sabendo que M é o ponto médio de AB. 3x 2 5 a) 16 A M B ___ Se M é o ponto médio de AB , então AM 5 MB. Assim, 3x 2 5 5 16 V 3x 5 16 1 5 V 21 V 3x 5 21 V x 5 __ 5 7 3 b) 3o passo 4x 2 12 M ___ M B O triângulo construído é isósceles. 9 Considere três retas coplanares distintas: r, s e t. Sabe-se que as retas r e s são perpendiculares à reta t. Qual é a posição relativa entre as retas r e s? 2x 1 30 A A B Se M é o ponto médio de AB , então AM 5 MB. Assim, 4x 2 12 5 2x 1 30 V 4x 2 2x 5 30 1 12 V 42 V 2x 5 42 V x 5 ___ 5 21 2 r s 100 c) t 2,5x 1 10 A M B ___ AM 1 MB 5 AB. Se M é o ponto médio de AB , então AM 5 MB. Assim, (2,5x 1 10) 1 (2,5x 1 10) 5 100 V V 5x 1 20 5 100 V 5x 5 100 2 20 V 5x 5 80 V 80 V x 5 ___ 5 16 5 18 M A B 16 M Atividades para casa B A Por dois pontos só é possível passar uma reta, e um segmento. A B 11 Desenhe, em seu caderno, quatro pontos distintos, A, B, C e D, sobre uma reta r. 4x � 20 A 45 ___ AM 1 MB 5 AB. Se M é o ponto médio de AB , então AM 5 MB. Assim, 2x 2 24 5 18 1 18 V V 12x 2 24 5 36 V 12x 5 36 1 24 V 12x 5 60 V 60 V x 5 ___ 5 5 12 e) Página 10 Considere dois pontos distintos A e B. Quantas retas podem passar por esses dois pontos? Quantos segmentos esses pontos determinam? 12x 2 24 d) As retas r e s são paralelas. B ___ AM 1 BM 5 AB. Se M é o ponto médio de AB , então AM 5 MB. Assim, 4x 1 20 5 16 1 16 V V 4x 1 20 5 32 V 4x 5 32 2 20 V 4x 5 12 V 12 V x 5 __ 5 3 4 ___ segmento AB qual- 8 Desenhe em seu caderno um quer. Determine com régua e compasso o ponto médio desse segmento. Nomeie esse ponto ___ de M. Trace por M uma reta perpendicular a AB. Construa um triângulo cujos vértices sejam A, B e um ponto da última reta construída. Que tipo de triângulo é esse? 1o passo A A B C D r a) Quantos segmentos esses quatro pontos determinam? Seis segmentos. b) Quais são os segmentos que esses quatro pon___tos ___determinam? ___ ___ ___ ___ , AD , BC , BD e CD . AB , AC 12 Desenhe, em seu caderno, quatro pontos distintos de modo que sejam vértices de um quadrilátero qualquer. Quantos segmentos esses pontos determinam? A B B 2o passo A M B C D ___ ___ ___ ___ ___ ___ , AD , BC , BD e CD . Seis segmentos: AB , AC 39 3P_YY_M8_RA_C02_038a067.indd 39 20.10.08 10:59:28 resolução de atividades Capítulo 2 13 Observe a figura e responda às questões em seu caderno. r s t 17 Desenhe em seu caderno quatro pontos distintos A, B, C e D, nessa ordem, sobre uma re- ta r. Se AC 5 36 cm, BC 5 13 cm e BD 5 25 cm, calcule as medidas AB, CD e AD. r A a) Quais são os pares de retas concorrentes? São pares de retas concorrentes r e u, r e t, s e u, s e t, t e u. b) Qual é o par de retas paralelas? O par de retas paralelas é r e s. A T U P D ___ ___ ___ ___ ___ ___ e AB MN , CD e OP , TU e EF a) Duas retas concorrentes têm um único ponto em comum. V b) Duas retas concorrentes são coplanares. V c) Duas retas coplanares são concorrentes. F — Duas retas coplanares podem ser paralelas. d)Se duas retas não são coplanares, então elas são reversas. V e) Se duas retas não têm ponto em comum, então elas são paralelas. F — Duas retas que não possuem ponto em comum podem ser paralelas ou reversas. em seu ca- x A 30 2 2x M 3x 2 14 x C B AC 1 CB 5 AB. Assim, 3x 2 14 1 x 5 34 V 48 V 4x 5 34 1 14 V 4x 5 48 V x 5 ___ 5 12 4 b) 56 2 7x A 3x x11 C B B ___ AM 1 MB 5 AB. Se M é o ponto médio de AB , então AM 5 MB. Assim, (30 2 2x) 1 (30 2 2x) 5 x V V 30 1 30 2 2x 2 2x 5 x V 60 2 4x 5 x V V 24x 2 x 5 260 V 25x 5 260 V 5x 5 60 V 60 V x 5 ___ 5 12 5 ___ 19 Na figura abaixo, os pontos assinalados sobre AB dividem-no em segmentos de mesma medida. 3x 2 12 15 Verifique se as afirmações a seguir são verdadeiras e justifique as falsas em seu caderno. ___ de AB, calcule 34 AC 1 CB 5 AB. Assim, 3x 1 x 1 1 5 56 2 7x V V 4x 1 1 5 56 2 7x V 4x 1 7x 5 56 2 1 V 55 V 11x 5 55 V x 5 ___ 5 5 11 F E 16 Sendo M o ponto médio ___ derno a medida de AB. a) C B O C 18 Determine em seu caderno o valor de x em cada caso a seguir. A 14 Com o auxílio de uma régua, identifique em seu caderno os segmentos congruentes. M D Se AC 5 36 cm e BC 5 13 cm, então AB 5 36 2 13 5 5 23 cm. Se BD 5 25 cm e BC 5 13 cm, então CD 5 5 25 2 13 5 12 cm. Logo AD 5 23 1 13 1 12 5 48 cm. u N B x12 C A D B ___ Determine, em seu caderno, a medida de CD , em centímetros. Como os segmentos são congruentes, então 3x 2 12 5 x 1 2 V 3x 2 x 5 2 1 12 V 2x 5 14 V 14 V x 5 ___ 5 7. Substituindo o valor de x na expres2 são x 1 2, conclui-se que cada segmento mede ___ 7 1 2 5 9 cm. Como o segmento CD tem a medida de três desses segmentos, ele mede 3 ? 9 5 27 cm. ___ 20 Nas figuras abaixo, M é ponto médio de AB . Calcule em seu caderno o valor das incógnitas de cada item. 2x 1 y a) A x12 M y11 B AM 1 MB 5 AB. Assim, 2x 1 y 5 (x 1 2) 1 (y 1 1) V V 2x 1 y 2 x 2 y 5 2 1 1 V ___x 5 3. Se M é o ponto médio de AB , então AM 5 MB, de forma que se tem x 1 2 5 y 1 1 Substituindo o valor de x 5 3 & 3 1 2 5 y 1 1 V V 5 5 y 1 1 V 5 2 1 5 y V y 5 4 b) 2y 1 2 A 3x 2 y M x13 B ___ Se M é o ponto médio de AB , então AM 5 MB. Assim, 3x 2 y 5 x 1 3 V 2y 5 x 1 3 2 3x V V 2y 5 22x 1 3 V y 5 2x 2 3 40 3P_YY_M8_RA_C02_038a067.indd 40 20.10.08 10:59:29 resolução de atividades Capítulo 2 Como AM 1 MB 5 AB tem-se (3x 2 y) 1 (x 1 3) 5 5 2y 1 2 V 4x 2 3y 5 21 V 3y 2 4x 5 1. Substituindo o valor de y 5 2x 2 3 & 3 ? (2x 2 3) 2 4x 5 5 1 V 6x 2 9 2 4x 5 1 V 2x 5 10 V x 5 5. Substituindo o valor de x para encontrar y & y 5 5 2x 2 3 V y 5 2 ? 5 2 3 V y 5 10 2 3 V y 5 7 21 Em seu caderno, determine a medida ___ M o ponto médio de AB. b) B 60° ___ de AB, sendo A x 3x 2 y y23 A 24° O 2x 2 9 M B ___ de AB tem-se AM 5 MB. Assim, Se M é o ponto médio y 2 3 5 2x 2 9 V y 5 2x 2 9 1 3 V y 5 2x 2 6. Como AM 1 MB 5 AB tem-se 3x 2 y 5 5 y 2 3 1 2x 2 9. Substituindo o valor de y 5 2x 2 6 na expressão & 3x 2 (2x 2 6) 5 (2x 2 6) 2 3 1 2x 2 9 V V 3x 2 2x 1 6 5 2x 2 6 2 3 1 2x 2 9 V x 1 6 5 4x 2 18 V x 2 4x 5 218 2 6 V 24 23x 5 224 V 3x 5 24 V x 5 ___ 5 8. 3 Substituindo o valor de x para encontrar y & y 5 5 2x 2 6 V y 5 2 ? 8 2 6 V y 5 16 2 6 V y 5 10. Como o segmento AB mede 3x 2 y, tem-se que AB 5 5 3 ? 8 2 10 5 24 2 10 5 14. x 1 24° 5 60° V x 5 60° 2 24° V x 5 36° c) A B x O 32° x 1 32° 5 90° V x 5 90° 2 32° V x 5 58° d) 110° B 22 Observe os pontos sobre uma reta r. 24 cm C A M B 32 cm 2x 2 20° N Sabe-se que AB é o ___ triplo de BC e BC é o dobro de CN. Quanto mede ND ? Chamando BC de x, tem-se AB 5 3x, pois AB é o triplo de BC. Assim, AB 1 BC 5 32 V 3x 1 x 5 32 V 32 V 4x 5 32. Então x 5 BC 5 ___ 5 8 4 Como BC mede o dobro de CN, então CN 5 4 cm. Como BC 1 CN 1 ND 5 24, tem-se 8 1 4 1 ND 5 5 24 V ND 5 24 2 8 2 4 V ND 5 12 cm 23 Desenhe em seu caderno seis pontos colineares e distintos A, B, C, D, M e N, de ___tal modo que M seja o , N o ponto médio do ponto médio ___do segmento AB ____ segmento CD e a medida de MN seja igual a 28 mm. Resposta possível. 28 mm A M B C N D Módulo 2: Ângulos Página 50 Atividades para classe 1 Determine em seu caderno o valor de x em cada caso. B a) O 18° x 5 26° 1 18° V x 5 44° A O (2x 2 20°) 1 (x 1 10°) 5 110° V 3x 2 10° 5 110° V 120 5 40º V 3x 5 110° 1 10° V 3x 5 120° V x 5 ____ 3 2 Determine em seu caderno o valor de x em cada caso. a) 6x 1 18° 6x 1 18° 5 90° V 6x 5 90° 2 18° V 6x 5 72° V 72° 5 12° V x 5 ____ 6 b) 110° 2 2x 4x 1 10° Note que a soma dos dois ângulos é 180°. Assim, (110° 2 2x) 1 (4x 1 10°) 5 180° V V 2x 1 120° 5 180° V 2x 5 180° 2 120° V 60° 5 30°. V 2x 5 60° V x 5 ____ 2 c) 170° 2 2x 3x 1 40° x 26° x 1 10° D A Os dois ângulos assinalados são opostos pelo vértice, e portanto são congruentes. Assim, 170° 2 2x 5 3x 1 40° V 22x 2 3x 5 40° 2 170° V 130° V 25x 5 2130° V 5x 5 130° V x 5 _____ 5 26°. 5 41 3P_YY_M8_RA_C02_038a067.indd 41 20.10.08 10:59:29 resolução de atividades Capítulo 2 3 Calcule em seu caderno o valor de x nas seguintes equações. 15° a) 2x 2 15° 5 0° V 2x 5 15° V x 5 ___ 5 2 14° 1 60’ _________ 5 5 7° 30’ 2 5 Determine em seu caderno o valor de x e de y. x1y 2x 2 40° b) 3x 2 54° 5 15° V 3x 5 15° 1 54° V 3x 5 69° V 69° 5 23° V x 5 ____ 3 x 1 y 5 90° V y 5 90° 2 x A soma dos três ângulos é 180°. Assim, (2x 2 40°) 1 (x 1 y) 1 (y 1 4°) 5 180°. Substituindo y 5 90° 2 x na expressão, (2x 2 40°) 1 90° 1 (90° 2 x 1 4°) 5 180° V V 2x 2 40° 1 90° 1 90° 2 x 1 4° 5 180° V V x 1 144° 5 180° V x 5 180° 2 144° V x 5 36°. Substituindo o valor de x para encontrar y & & y 5 90° 2 36° V y 5 54°. c) 5x 1 30° 5 60° V 5x 5 60° 2 30° V 5x 5 30° V 30° 5 6° V x 5 ____ 5 d)2x 5 x 1 125° V 2x 2 x 5 125° V x 5 125° 4 ___ Calcule em seu caderno o valor de x, sabendo que OP é bissetriz de A OB . a) A P y 1 4° ___ Q 20° C B 3x 2 10° O ___ B , e OQ 6 Na figura seguinte, OP é bissetriz de AO é bissetriz de B OC . Se P OQ 5 65°, quanto mede A OC ? B ___ é bissetriz de A OP O B, então 3x 2 10° 5 20° V P 30° 5 10°. V 3x 5 20° 1 10° V 3x 5 30° V x 5 ____ 3 b) A O A ___ B Se OP é bissetriz de ___ A O B, então A O P 5 PO . De maneira análoga, se OQ é bissetriz de BOC , então P 58° C. Assim, AO C 5 AO P 1 PO B 1 BO Q 1 B O Q 5 QO P 5 P 1 Q O C. Como AO O B e B O Q 5 Q O C, a soma C 5 PO B B pode ser escrita como AO 1 PO 1 B O Q 1 1 BO Q 5 2 ? (PO B 1 BO Q). Tem-se que P O Q 5 5 P O B 1 B O Q 5 65°, assim A O C 5 2 ? 65° 5 130°. 5x 2 24° O B ___ é bissetriz de A OP O B, então 5x 2 24° 5 2 ? 58° V 5x 2 24° 5 116° V 5x 5 116° 1 24° V 5x 5 140° V 140° 5 28°. V x 5 _____ 5 Página 51 Atividades para casa 7 Observe a figura abaixo e, em seu caderno, escreva quanto mede cada ângulo pedido. C c) B B D P O A A 3x 2 21° B mede 90°. Assim, PO A mede 45°. O ângulo AO O ângulo em destaque na figura é igual ao supleA mentar de PO . Assim, 3x 2 21° 5 180° 2 45° V V 3x 2 21° 5 135° V 3x 5 135° 1 21° V 3x 5 156° V 156° 5 52°. V x 5 _____ 3 a) A O B 5 40° O C 5 90° b)A O D 5 150° c) A O C 5 90° 2 40° 5 50° d)B O D 5 150° 2 40° 5 110° e) B O D 5 150° 2 90° 5 60° f) C 42 4P_YY_M8_RA_C02_038a067.indd 42 29.10.08 14:39:13 resolução de atividades Capítulo 2 8 Escreva, em seu caderno, uma expressão algébrica que represente cada situação. a) A soma de dois ângulos é 50°. Sendo x um dos ângulos e y o outro & x 1 y 5 50°. b) A diferença entre dois ângulos é 36°. Sendo x um dos ângulos e y o outro & x 2 y 5 36°. c) A soma de um ângulo com a metade desse ângulo é 126°. 1 1 x 5 Sendo x o ângulo, sua metade será __ x & x 1 __ 2 2 5 126°, ou x 1 0,5x 5 126°. d)A terça parte de um ângulo é 20°. 1 Sendo x o ângulo, sua terça parte será __ x & 3 x __ & 5 20°, ou x ; 3 5 20°. 3 e) O triplo da metade de um ângulo é 12°. x 1 Sendo x o ângulo, sua metade será __ x & 3 ? __ 5 12°, 2 2 ou 3 ? (x ; 2) 5 12°. f) A metade da terça parte de um ângulo é igual a 10°. 1 Sendo x o ângulo, sua terça parte será __ x & 3 x x 1 & __ ; 2 5 10° V __ ? __ 5 10° V 3 3 2 x __ V 5 10°, ou (x ; 3) ; 2 5 10°. 6 g)A terça parte de um ângulo é 18°. 1 x Sendo x o ângulo, sua terça parte será __ x & __ 5 18°, 3 3 ou (x ; 3) 5 18°. h)A soma da metade de um ângulo com a quinta parte deste ângulo é 23°. 1 Sendo x o ângulo, sua quinta parte será __ x, e sua me5 x __ x 1 __ __ ou (x ; 2) 1 (x ; 5) 5 23°. tade, x & 1 5 23°, 2 2 5 9 Calcule em seu caderno o valor de cada incógnita a seguir. a) x 40° 3a 1 10° 5 70° (ângulos opostos pelo vértice) V 60° 5 20° V 3a 5 70° 2 10° V 3a 5 60° V a 5 ____ 3 5b 2 40° 1 70° 5 180° V 5b 1 30° 5 180° V 150° 5 30° V 5b 5 180° 2 30° V 5b 5 150° V b 5 _____ 5 10 A soma de um ângulo com a terça parte do ângulo reto é igual a 90°. Determine, em seu caderno, a medida desse ângulo. A terça parte do ângulo reto mede 90° ; 3 5 30°. Assim, x 1 30° 5 90° V x 5 90° 2 30° 5 60°. 11 A diferença entre 180° e um ângulo é igual ao dobro da diferença entre 90° e 20°. Calcule em seu caderno a medida desse ângulo. Seja x o ângulo. 180° 2 x 5 2 ? (90° 2 20°) V V 180° 2 x 5 2 ? 70° V 180° 2 x 5 140° V V 180° 2 140° 5 x V x 5 40° 12 Determine em seu caderno. a) Um ângulo cuja medida é metade do ângulo reto. O ângulo reto mede 90°. Assim, um ângulo que mede a metade de um ângulo reto medirá 90° ; 2 5 45°. b) Um ângulo cuja medida é um terço de um ângulo raso. O ângulo raso mede 180°. Assim, um ângulo que mede um terço de um ângulo raso medirá 180° ; 3 5 60°. c) Um ângulo cuja medida é o dobro do ângulo reto. O ângulo reto mede 90°. Assim, um ângulo que mede o dobro de um ângulo reto medirá 2 ? 90° 5 180°. 13 Calcule ___ em seu caderno a medida de A O B, sabendo que OP é bissetriz de A O B. a) B x 1 40° 5 180° V x 5 180° 2 40° V x 5 140° P b) 2x 3y 2 14° 52° 3x 2 10° O 3y 2 14° 5 52° (ângulos opostos pelo vértice) V 66° 5 22° V 3y 5 52° 1 14° V 3y 5 66° V y 5 ____ 3 c) 4x 1 30° 4x 1 30° 1 90° 5 180° V 4x 1 120° 5 180° V 5 15° V 4x 5 180° 2 120° V 4x 5 60° V x 5 ____ 60° 4 d) 5b 2 40° 3a 1 10° 70° 1 8° A ___ B, então 2x 1 8° 5 3x 2 10° V é bissetriz de A O OP V 8° 1 10° 5 3x 2 2x V x 5 18°. O B 5 (2x 1 8°) 1 (3x 2 10°) 5 2 ? (2x 1 Tem-se que A 1 8°). Substituindo o valor de x na expressão, A O B 5 B 5 2 ? (2 ? 18° 1 8°) V A O 5 2 ? (36° 1 8°) 5 2 ? 44° V B V A O 5 88°. b) B 2x 1 3° O P 6x 2 24° A ___ é bissetriz de A OP O B, então A O B 5 2 ? (2x 1 3°). B 5 6x 2 24° (ângulos opostos pelo Além disso, A O 43 3P_YY_M8_RA_C02_038a067.indd 43 20.10.08 10:59:30 resolução de atividades Capítulo 2 vértice). Então se tem 6x 2 24° 5 2 ? (2x 1 3°) V V 6x 2 24° 5 4x 1 6° V 6x 2 4x 5 6° 1 24° V 30° 5 15°. V 2x 5 30° V x 5 ____ 2 Como A O B 5 2 ? (2x 1 3°), substituindo o valor de x na expressão tem-se A O B 5 2 ? (2 ? 15° 1 3°) 5 2 ? 33° V B 5 66°. V A O c) P Substituindo o valor de y na expressão x 5 y 2 10° & & x 5 35° 2 10° V x 5 25°. Assim, x 5 25° e y 5 35°. Página 52 15 Efetue em seu caderno. a) (60° 42’ 30”) 1 (40° 18’ 41”) B 1 x 1 16° 3x 2 22° A ___ B, então é bissetriz de A O OP (x 1 16°) 1 (x 1 16°) 1 (3x 2 22°) 5 180° V V 5x 1 10° 5 180° V 5x 5 180° 2 10° V 170º 5 34º. V 5x 5 170° V x 5 _____ 5 Como A O B 5 (x 1 16°) 1 (x 1 16°), substituindo o valor de x na expressão, tem-se B 5 100°. A O B 5 34° 1 16° 1 34° 1 16° V A O ___ O B, determine em 14 Sabendo que OP é bissetriz de A 1 B x 1 5° y 2x 1 y A soma dos três ângulos é 180°. Assim, (x 1 5°) 1 y 1 (2x 1 y) 5 180°. Substituindo o valor de x 5 y 2 5° na expressão & & (y 2 5° 1 5°) 1 y 1 [2 ? (y 2 5°) 1 y] 5 180° V V y 2 5° 1 5° 1 y 1 2y 2 10° 1 y 5 180° V V 5y 2 10° 5 180° V 5y 5 180° 1 10° V 5y 5 190° V 190° 5 38°. V y 5 _____ 5 Substituindo o valor de y na expressão x 5 y 2 5° & & x 5 38° 2 5° V x 5 33°. Assim, x 5 33° e y 5 38°. A P 2x 1 2y x 1 5° 2 39° 91’ 86’’ 18° 40’ 36’’ 21° 51’ 50” c) 5 ? (16° 20’ 40”) 20’ 40’’ 35 80° 100’ 200’’ & 100’ 5 1° 40’ 1 1° 40’ 3’ 20’’ & 200’’ 5 3’ 20’’ 81° 43’ 20” d)(18° 43’ 28”) : 4 2 18° 43’ 28’’ 4 16° 4° 40’ 52’’ 2° 120’ 1 43’ 163’ 2 160’ 3’ 180’’ 1 28’’ 208’’ 2 208’’ 0’’ 16 Calcule em seu caderno a) O triplo de 46° 31’ 42’’ y 2 5° O 30’’ 41’’ 71’’ 11’’ & 71’’ 5 1’ 11’’ 11’’ & 61’ 5 1° 1’ 11” Transforma–se 40° 32’ 26’’ em 39° 91’ 86’’, pois não é possível subtrair 40’ de 32’ e nem 36’’ de 26’’. Assim, 16° O ___ A é bissetriz de A OP O B, então x 1 5° 5 y V x 5 y 2 5°. b) 100° 1° 101° 42’ 18’ 60’ 1’ 61’ 1’ 1’ b) (40° 32’ 26”) 2 (18° 40’ 36”) seu caderno o valor de x e y. P 60° 40° 100° 1 O a) Atividade para casa 46° 31’ B ___ OP O B, então x 1 5° 5 y 2 5° V é bissetriz de A V x 5 y 2 5° 2 5° V x 5 y 2 10°. A soma dos três ângulos é 180°. Assim, (2x 1 2y) 1 (x 1 5°) 1 (y 2 5°) 5 180°. Substituindo o valor de x 5 y 2 10° na expressão & & [2 ? (y 2 10°) 1 2y] 1 (y 2 10° 1 5°) 1 1 (y 2 5°) 5 180° V 2y 2 20° 1 2y 1 y 2 10° 1 5° 1 1 y 2 5° 5 180° V 6y 2 30° 5 180° V 6y 5 210° 5 180° 1 30° V 6y 5 210° V y 5 _____ 5 35°. 6 42’’ 33 138° 93’ 126’’ & 93’ 5 1° 33’ 1 1° 33’ 2’ 6’’ & 126’’ 5 2’ 6’’ 139° 35’ 6” b) O dobro de 134° 14’ 21’’ 134° 14’ 21’’ 32 268° 28’ 42’’ 44 3P_YY_M8_RA_C02_038a067.indd 44 20.10.08 10:59:31 resolução de atividades Capítulo 2 c) A metade de 56° 18’ 14’’ 56° 18’ 14’’ 2 56° 18’ 14’’ 0° 0’ 0’’ 2 28° 9’ 7’’ ___ 19 Determine a medida de A O B, sabendo que ON é bissetriz de AO B. A d)Um terço de 139° 17’ 15’’ 139° 17’ 2 138° 15’’ 3 46° 25’ 45’’ 1° 60’ 1 17’ 77’ 2 75’ 2’ 120’’ 1 15’’ 135’’ 2 135’’ 0’’ N 22° 16’ 43’’ O B ___ Se ON é bissetriz de AO B, então AO B 5 2 ? NO B V V AO B 5 2 ? (22° 16’ 43”) 5 44° 33’ 26”. 20 Determine em seu caderno o valor de b. e) Um quarto de 194° 16’ 48’’ 194° 16’ 48’’ 4 2 192° 48° 34’ 12’’ 2° 120’ 1 16’ 136’ 2 136’ 0’ 48’’ 2 48’’ 0’’ 17 Dois ângulos opostos pelo vértice têm suas medidas expressas por 3x 2 36° e 60° 2 3x. Calcule a soma desses ângulos. b 17° 11’ 14’’ b 5 90° 2 17° 11’ 14’’ 5 89° 59’ 60’’ 2 17° 11’ 14’’ 5 5 72° 48’ 46” 21 Construa, em seu caderno, um triângulo ABC qualquer. a) Determine, com régua e compasso, os pontos ___ ___ ___ , AC e BC . médios dos lados AB A Como são opostos pelo vértice, os ângulos são congruentes & 3x 2 36° 5 60° 2 3x V 6x 5 96° V V x 5 16°. A soma dos dois ângulos é (3x 2 36°) 1 (60° 2 3x) 5 5 2 ? (3x 2 36°) 5 2 ? (3 ? 16° 2 36°) 5 5 2 ? 12° 5 24° C B b) Desenhe os segmentos cujas extremidades são um vértice do triângulo e o ponto médio do lado oposto a esse vértice. A 18 Calcule em seu caderno o valor de x. a) 3x 2 31’ 5 37° 37° 31’ 3x 5 37° 1 31’ V 3x 5 37° 31’ V x 5 ______ 5 3 36° 1 90’ 1 60” ________________ 5 5 12° 30’ 20” 3 b) 8x 5 1’ 4’’ 64” 1’ 4” ____ x 5 _____ 5 5 8” 8 8 c) x 1 59’ 55’’ 5 121° x 5 121° 2 59’ 55’’ 5 120° 59’ 60’’ 2 59’ 55’’ V V x 5 120° 5’’ C B c) O que você observou? Os segmentos são concorrentes em um único ponto. 22 Construa, em seu caderno, um triângulo ABC qualquer. a) Determine, com régua e compasso, os pontos ___ ___ ___ médios dos lados AB , AC e BC . A d)x 2 10’ 5 10° 10’’ x 5 10° 10’’ 1 10’ V x 5 10° 10’ 10’’ e) x 1 10’ 5 16° x 5 16° 2 10’ 5 15° 60’ 2 10’ V x 5 15° 50’ C B 45 4P_YY_M8_RA_C02_038a067.indd 45 29.10.08 14:39:31 resolução de atividades Capítulo 2 ___ ___ b) ___ Nomeie de M, N e P os pontos médios de AB , AC, BC , respectivamente. A N M C P B ___ c) Construa por M a reta perpendicular ao lado AB , ___ por N a perpendicular ao lado AC e,___ finalmente, por P a reta perpendicular ao lado BC . A Substituindo x 5 132° 2 2y & 2y 2 48° 5 5 (132° 2 2y) 2 y V 2y 2 48° 5 132° 2 3y V V 2y 1 3y 5 132° 1 48° V 5y 5 180° V 180° V y 5 _____ 5 36° 5 Voltando em x 5 132° 2 2y & x 5 132° 2 2 ? 36° V V x 5 132° 2 72° V x 5 60° (x 1 y) 1 a 1 (x 2 y) 5 180° V 2x 1 a 5 180° V V 2 ? 60° 1 a 5 180° V 120° 1 a 5 180° V V a 5 180 2 120° V a 5 60° d) N M P 58° 2 x C 4x 2 27° B d)O que você observou? As retas assim construídas são concorrentes em um único ponto. 23 Determine em seu caderno a medida de a . a) a 1 8° a (a 1 8°) 1 90° 1 a 5 180° V 2a 1 98° 5 180° V 82° 5 41° V 2a 5 180° 2 98° V 2a 5 82° V a 5 ____ 2 b) Tem–se o seguinte sistema de equações. 58° 2 x 1 a 5 90° 4x 2 27° 1 a 5 90° Multiplicando a primeira das equações do sistema 232° 2 4x 1 4a 5 360° por 4 tem–se 4x 2 27° 1 a 5 90° Somando agora as duas equações tem–se 5a 1 4x 2 4x 1 232° 2 27° 5 360° 1 90° Os termos envolvendo a variável x se anulam, de forma que a equação resultante é 5a 1 205° 5 450° V 5a 5 245° V 245° 5 49° V a 5 _____ 5 e) 2 2 5x 1 y a 3x 1 2° y 1 22° a c) 2y 2 48° x1y 2x 1 2y • y 1 22° 5 3x 1 2° (opostos pelo vértice) V V y 5 3x 1 2° 2 22° V y 5 3x 2 20° •(3x 1 2°) 1 (5x 1 y) 5 180° V 3x 1 2° 1 5x 1 1 3x 2 20° 5 180° V 11x 2 18° 5 180° V 11x 5 198° 5 180° 1 18° V 11x 5 198° V x 5 _____ 5 18° 11 Substituindo em y 5 3x 2 20° & y 5 3 ? 18° 2 20° V V y 5 54° 2 20° V y 5 34° a 5 5x 1 y (opostos pelo vértice) V a 5 5 5 ? 18° 1 34° V a 5 90° 1 34° 5 124° x1y a a x2y 132° 2 y •x 1 y 5 132° 2 y (opostos pelo vértice) V V x 5 132° 2 y 2 y V x 5 132° 2 2y •2y 2 48° 5 x 2 y (opostos pelo vértice) (x 1 y) 1 (2x 1 2y) 5 90° V 3x 1 3y 5 90° V 90° V 3 ? (x 1 y) 5 90° V x 1 y 5 ____ 5 30° 3 Como a 5 x 1 y (opostos pelo vértice), tem–se a 5 x 1 y 5 30° 24 Encontre o valor numérico de cada expressão abaixo, considerando A 5 6° 12’’, B 5 88°, C 5 12’ 35’’ e D 5 120° 3’. a) 2A 1 B 2 ? (6° 12’’) 1 88° 5 12° 24’’ 1 88° 5 100° 24” b) 3 (A 1 D) 2 (B 1 D) 3 ? (6° 12’’ 1 120° 3’) 2 ( 88° 1 120° 3’) 5 5 3 ? (126° 3’ 12’’) 2 208° 3’ 5 5 378° 9’ 36’’ 2 208° 3’ 5 5 170° 6’ 6” c) 5 [A 1 40’ 2 (B 2 80°)] 1 2 (C 1 D) 5 ? [6° 12’’ 1 40’ 2 (88° 2 80°)] 1 1 2 ? (12’ 35’’ 1 120° 3’) 5 5 ? [ 6° 40’ 12’’ 2 8°] 1 1 2 ? (120° 15’ 35’’) 5 5 ? [21° 19’ 48’’] 1 240° 31’ 10’’ 5 5 26° 39’ 1 240° 31’ 10’’ 5 233° 52’ 10” 46 3P_YY_M8_RA_C02_038a067.indd 46 20.10.08 10:59:32 resolução de atividades Capítulo 2 Página 53 ___ Atividades para casa 25 Utilizando régua e compasso, transporte o ângulo abaixo em seu caderno e, depois, faça o que se pede em cada item. B B. Se ___ OP é bissetriz de A O , então A O P 5 P O O C. Se OQ é bissetriz de B O C, então B O Q 5 Q C 5 A C 5 A O O P 1 P O B 1 B O Q 1 Q O C V A O B 1 B O B 1 P O B 1 B O Q 1 B O Q 5 2 ? (P O O Q). 5 P 150° C 5 150°, tem-se P O B 1 B O Q 5 _____ Como A O 5 2 5 75°, e P O Q 5 P O B 1 B O Q 5 75° 27 Desenhe um segmento de extremidades A e B e determine o ponto médio desse segmento. Construa pelo ponto médio a perpendicular ao segmento. Assinale um ponto qualquer sobre essa perpendicular e o nomeie de P. Com a ponta–seca do compasso em P e abertura igual a PA, trace uma circunferência. O que você observou? a) Trace a bissetriz desse ângulo. P B A M A M P B A M B A circunferência também passa pelo ponto B, logo PA 5 PB. b) Marque um ponto qualquer da bissetriz e o nomeie de P. 28 Desenhe em seu caderno um triângulo qualquer e construa as bissetrizes dos ângulos internos desse triângulo. O que você observou? As bissetrizes são concorrentes em um único ponto. P c) Construa por P as perpendiculares aos lados do ângulo. A P B d)Sejam A e B os pontos onde as perpendiculares ___ ___ cruzam os lados do ângulo. Meça PA e meça PB . O que você conclui? PA 5 PB ___ 29 Desenhe em seu caderno uma ___ circunferência de diâmetro BC . Construa um triângulo ABC, com o vértice A pertencente à circunferência. A B C a) Meça o ângulo B C A com um transferidor. Qual é a medida desse ângulo? 90° b) Compare a sua resposta com a de seus colegas. O que você pode concluir a respeito das respostas encontradas? O triângulo ABC é retângulo em A e isso independe da posição do ponto A sobre a circunferência. 30 Em seu caderno, calcule a medida do menor ângulo presente na figura a seguir. ___ O B e OQ é bis26 Na figura a seguir, OP é bissetriz de A C C 5 150°, quanto mede P O Q? setriz de B O . Se A O 144° 2 4x 3x 1 10° 4x 1 4° Q B 54° 5x 1 4° C P A O (3x 1 10°) 1 (144° 2 4x) 1 (4x 1 4°) 1 (5x 1 4°) 1 1 54° 5 360° V 8x 1 216° 5 360° V V 8x 5 360° 2 216° V 8x 5 144° V 144° V x 5 _____ 5 18° 8 47 3P_YY_M8_RA_C02_038a067.indd 47 20.10.08 10:59:32 resolução de atividades Capítulo 2 Assim os ângulos desconhecidos medem • 3x 1 10° 5 3 ? 18° 1 10° 5 54° 1 10° 5 64° • 144° 2 4x 5 144° 2 4 ? 18° 5 144° 2 72° 5 72° • 4x 1 4° 5 4 ? 18° 1 4 5 72° 1 4° 5 76° • 5x 1 4° 5 5 ? 18° 1 4° 5 90° 1 4° 5 94° Desse modo, o menor ângulo é o que mede 54°. 31 No gráfico de setores mostrado abaixo, a razão entre a área de cada uma das partes e a área total está indicada percentualmente em cada parte. 10% % a) 20% os dois ponteiros estão sobrepostos. A partir desse instante há dois ângulos formados por eles dividindo a circunferência em duas partes, sendo que enquanto um dos ângulos vai aumentando a sua abertura o outro vai diminuindo. O primeiro ângulo aumenta até que, em um determinado momento, passa a medir 90°, e posteriormente o segundo vai diminuindo até medir também 90°. Desse modo, durante uma hora, os ponteiros formam ângulos retos por duas vezes, e consequentemente em 24 horas os ponteiros formam ângulos retos 48 vezes. 10% 20% a a Módulo 3: Pares de ângulos Página 25% 12,5% 12,5% Determine, em seu caderno, a medida do ângulo indicado por a. O percentual correspondente ao ângulo a é 100% 2 20% 2 10% 2 25% 2 12,5% 5 32,5% Assim, a corresponde a 32,5% de 360°, ou seja, a 5 0,325 ? 360° 5 117° b) 57 Atividades para classe 1 Observe a figura e responda às questões em seu caderno. t a b d 50% r c x 50% y w x s z y y Determine as medidas x e y sabendo que y é quatro vezes a medida x. x 1 y 5 50%. Se y 5 4x, então x 1 4x 5 50% V V 5x 5 50% V x 5 10%; y 5 4x 5 4 ? 10% 5 40%. Então x corresponde a 10% de 360°, ou seja: x 5 0,1 ? 360° 5 36°. E y corresponde a 40% de 360°, ou seja: y 5 0,4 ? 360° 5 144°. a) Quais pares de ângulos formados pelas retas r, s e t são correspondentes? São pares de ângulos correspondentes (a, x); (b, y); (c, z); (d, w). 32 O ângulo formado pelos ponteiros das horas e dos minutos do relógio a seguir ao marcar 9 horas é reto. c) Quais pares de ângulos formados pelas retas r, s e t são alternos externos? São pares de ângulos alternos externos (a, z); (b, w). b) Quais pares de ângulos formados pelas retas r, s e t são alternos internos? São pares de ângulos alternos internos (c, x); (d, y). d)Quais pares de ângulos formados pelas retas r, s e t são colaterais internos? São pares de ângulos colaterais internos (c, y); (d, x). e) Quais pares de ângulos formados pelas retas r, s e t são colaterais externos? São pares de ângulos colaterais externos (a, w); (b, z). 2 Nas figuras abaixo, as retas r e s são paralelas. Determine, em seu caderno, o valor de x. Determine em seu caderno quantas vezes os ponteiros das horas e dos minutos formam ângulo reto em um período de 24 horas. Determinando quantas vezes os ponteiros das horas e dos minutos formam um ângulo reto em 1 hora: Considera–se como ponto inicial o momento em que a) x r b) x 112° s 132° r s 48 4P_YY_M8_RA_C02_038a067.indd 48 29.10.08 14:39:48 resolução de atividades Capítulo 2 c) f) r r c) s r x s 3x � 18° 3x � 10° s 40° 130° 82° � 2x y f) r 2x � 38° s y 176° � x d) r g) r s s 4x � 50° 35° x e) h) s r 6x � 18° r 4x � 34° s x 2x � 92° a) Os ângulos são correspondentes. Então x 5 112°. b)Os dois ângulos são suplementares. Assim, x 1 132° 5 180° V x 5 180° 2 132° V x 5 48°. c)Os dois ângulos são alternos internos, portanto são congruentes & x 5 40°. d)Os dois ângulos são alternos externos, portanto são congruentes & x 5 35°. e)Os dois ângulos são alternos externos, portanto são congruentes & x 5 90°. f) Os dois ângulos são suplementares. Assim, (3x 2 10°) 1 130° 5 180° V V 3x 1 120° 5 180° V 3x 5 180° 2 120° V 60° 5 20°. V 3x 5 60° V x 5 ____ 3 g)Os dois ângulos são alternos externos, portanto são congruentes & 6x 1 18° 5 4x 1 50° V V 6x 2 4x 5 50° 2 18° V 2x 5 32° V 32° 5 16°. V x 5 ____ 2 h)Os dois ângulos são suplementares. Assim, (4x 1 34°) 1 (2x 1 92°) 5 180° V 6x 1 126° 5 5 180° V 6x 5 180° 2 126° V 6x 5 54° V 54° 5 9°. V x 5 ____ 6 3 Sabendo que as retas r e s são paralelas, determine o valor das incógnitas a seguir. a) r d) 32° r s 4x � 42° 98° � x y s x y b) y r 3x � 10° s 80° e) 3x � 8° 2x � 18° r s y a)O ângulo x e o ângulo de 32° são alternos externos, portanto são congruentes. Os ângulos x e y são suplementares, de forma que se tem x 1 y 5 180° V V 32° 1 y 5 180° V y 5 180° 2 32° V y 5 148° Assim, x 5 32° e y 5 148° b)Os ângulos (3x 1 10°) e 80° são suplementares, assim, (3x 1 10°) 1 80° 5 180° V 3x 1 90° 5 5 180° V 3x 5 180° 2 90° V 3x 5 90° V 90° 5 30° V x 5 ____ 3 Os ângulos (3x 1 10°) e y são opostos pelo vértice, ou seja, são congruentes. Assim, y 5 3x 1 10° V y 5 3 ? 30° 1 10° V y 5 5 90° 1 10° 5 100°. Logo, x 5 30° e y 5 100° c)Os ângulos (82° 2 2x) e (3x 2 18°) são alternos externos, portanto congruentes. Assim, 82° 2 2x 5 3x 2 18° V 82° 1 18° 5 3x 1 2x V 100° 5 x V x 5 20° V 100° 5 5x V _____ 5 Os ângulos (3x 2 18°) e y são suplementares. Assim, (3x 2 18°) 1 y 5 180° Substituindo x 5 20° & 3 ? 20° 2 18° 1 y 5 180° V 60° 2 18° 1 y 5 180° V V 42° 1 y 5 180° V y 5 180° 2 42° V y 5 138° Assim, x 5 20° e y 5 138° d)Os ângulos (4x 2 42°) e (98° 2 x) são alternos externos, portanto congruentes. Assim, 4x 2 42° 5 98° 2 x V 5x 5 98° 1 42° V 140° 5 28° V 5x 5 140° V x 5 _____ 5 Os ângulos y e (98° 2 x) são suplementares, assim, y 1 98° 2 x 5 180° Substituindo x 5 28° & y 1 98° 2 28° 5 180° V V y 5 180° 2 70° V y 5 110° Assim, x 5 28° e y 5 110° e)Os ângulos (2x 2 18°) e (3x 1 8°) são suplementares. Assim, (2x 2 18°) 1 (3x 1 8) 5 180° V V 5x 2 10° 5 180° V 5x 5 180° 1 10° V 190° V 5x 5 190° V x 5 _____ 5 38° 5 Os ângulos (2x 2 18°) e y são alternos externos e, portanto, congruentes. Assim, 2x 2 18° 5 y. Substituindo x 5 38° & 2 ? 38° 2 18° 5 y V V 76° 2 18° 5 y V y 5 58° Assim, x 5 38° e y 5 58° f)Os ângulos (2x 1 38°) e (176° 2 x) são alternos internos, então são congruentes. Assim, 2x 1 38° 5 176° 2 x V 2x 1 x 5 176° 2 38° V 138° V 3x 5 138° V x 5 _____ 5 46° 3 Os ângulos y e (176° 2 x) são suplementares, assim, y 1 (176° 2 x) 5 180°. Substituindo x 5 46° & & y 1 176° 2 46° 5 180° V y 1 130° 5 180° V V y 5 180° 2 130° V y 5 50° Assim, x 5 46° e y 5 50° 49 3P_YY_M8_RA_C02_038a067.indd 49 20.10.08 10:59:33 resolução de atividades Capítulo 2 4 Dois ângulos são suplementares e um é o triplo do outro. Calcule esses ângulos. Chamando um dos ângulos de x, o segundo, por ser o triplo do primeiro, será representado por 3x. As180° 5 45°; sim, x 1 3x 5 180° V 4x 5 180° V x 5 _____ 4 3x 5 3 ? 45° 5 135° Os ângulos medem 45° e 135°. 5 Dois ângulos são complementares e um excede o outro em 10°. Quanto mede cada ângulo? Chamando um dos ângulos de x, o outro será representado por x 1 10°. Assim, x 1 (x 1 10°) 5 90° V 2x 1 10° 5 90° V 2x 5 80° 5 40°; 5 90° 2 10° V 2x 5 80° V x 5 ____ 2 x 1 10° 5 40° 1 10° 5 50°. Os ângulos medem 50° e 40°. d) a x b s 7 Na figura, as retas r e s são paralelas e concorrem com a transversal t. Determine o valor de x. r x � 20° s r z 3x � 60° y x 48° 36° s Os ângulos y e 36° são alternos internos, ou seja, são congruentes. Os ângulos z e 48° também são alternos internos, sendo também congruentes. Os ângulos x, y e z somam 180°, assim, x 1 y 1 z 5 180° V x 1 36° 1 48° 5 180° V V x 1 84° 5 180° V x 5 180° 2 84° V x 5 96°. b) b a x 60° Traça–se uma reta paralela às demais, dividindo o ângulo x em dois (a e b). Os ângulos a e 160° são suplementares, portanto, a 5 180° 2 160° 5 20°. Os ângulos b e 60° são alternos internos, portanto b 5 60°. Assim, x 5 a 1 b V x 5 20° 1 60° V V x 5 80°. 6 Nas figuras abaixo, as retas r e s são paralelas. Calcule, em seu caderno, o valor de cada incógnita. a) 160° r c r 74° 46° s t Os ângulos são colaterais externos, ou seja, são suplementares. Assim, (x 1 20°) 1 (3x 1 60°) 5 180° V 4x 1 80° 5 180° V 100° V 4x 5 180° 2 80° V 4x 5 100° V x 5 _____ 5 25°. 4 Página 58 Atividades para casa 8 Sabendo que as retas r e s são paralelas, determine em seu caderno o valor de x em cada caso. a) 74° r 2x � 10° O ângulo a vale 74° (opostos pelo vértice). O ângulo b vale 46° (alternos internos). Como a 1 b 1 c 5 180°, tem–se 74° 1 46° 1 c 5 180° V c 1 120° 5 180° V V c 5 180° 2 120° V c 5 60°. Os ângulos x e c são correspondentes, então x 5 60°. s Os ângulos são alternos internos, ou seja, são congruentes. Assim, 2x 2 10° 5 74° V 2x 5 74° 1 10° V 84° 5 42°. V 2x 5 84° V x 5 ____ 2 b) 3x � 19° r c) Analogamente à atividade resolvida da página 56. r x 36° 2x � 26° s a b s 42° Traça–se uma reta paralela às demais, dividindo o ângulo x em dois (a e b). Os ângulos a e 36° são correspondentes, portanto a 5 36°. Os ângulos b e 42° são correspondentes, portanto b 5 42°. Assim, x 5 a 1 b V V x 5 36° 1 42° V x 5 78°. Os ângulos são suplementares. Assim, 2x 2 26° 1 3x 2 19° 5 180° V 5x 2 45° 5 180° V 225° V 5x 5 180° 1 45° V 5x 5 225° V x 5 _____ 5 45°. 5 c) r x � 60° 164° � x s 50 3P_YY_M8_RA_C02_038a067.indd 50 20.10.08 10:59:34 resolução de atividades Capítulo 2 Os ângulos são alternos internos, ou seja, são congruentes. Assim, x 1 60° 5 164° 2 x V x 1 x 5 104° 5 52° 5 164° 2 60° V 2x 5 104° V x 5 _____ 2 V y 5 180° 2 128° V y 5 52° Os ângulos x e 71° são colaterais internos, ou seja, são suplementares. Assim, x 1 71° 5 180° V V x 5 180° 2 71° V x 5 109° d) c) 3x � 24° r s y 192° � x Os ângulos são alternos externos, ou seja, são congruentes. Assim, 3x 1 24° 5 192° 2 x V 3x 1 x 5 168° 5 42° 5 192° 2 24° V 4x 5 168° V x 5 _____ 4 e) x � 20° 2x � 10° r s Os ângulos são colaterais internos, ou seja, são suplementares. Assim, 2x 2 10° 1 x 2 20° 5 180° V V 3x 2 30° 5 180° V 3x 5 180° 1 30° V 3x 5 210° 5 70° 5 210° V x 5 _____ 3 r s f) 210° � 4x 60° � 2x Os ângulos são congruentes. Assim, 210° 2 4x 5 5 60° 1 2x V 4x 1 2x 5 210° 2 60° V 6x 5 150° V 150° 5 25° V x 5 _____ 6 9 Determine em seu caderno as medidas dos ân___ gulos ___ x e y, sabendo que as retas suportes de AB e CD são paralelas. a) C D x y 46° 34° A B Os ângulos y e 34° são colaterais internos, ou seja, são suplementares. Assim, y 1 34° 5 180° V V y 5 180° 2 34° V y 5 146°. Os ângulos x e 46° são colaterais internos, ou seja, são suplementares. Assim, x 1 46° 5 180° V x 5 180° 2 46° V x 5 134° b) D C x 71° A D 128° y B Os ângulos y e 128° são colaterais internos, ou seja, são suplementares. Assim, y 1 128° 5 180° V C 39° x 20° A B Os ângulos y e 20° são colaterais internos, ou seja, são suplementares. Assim, y 1 20° 5 180° V V y 5 180° 2 20° V y 5 160° Os ângulos x e 39° são colaterais internos, ou seja, são suplementares. Assim, x 1 39° 5 180° V V x 5 180° 2 39° V x 5 141° 10 Duas retas paralelas determinam com uma reta transversal ângulos colaterais que medem 4x 1 12° e 6x 1 38°. Calcule, em seu caderno, os ângulos obtusos determinados por essas retas. Os dois ângulos são colaterais, portanto são suplementares. Assim, 6x 1 38° 1 4x 1 12° 5 180° V V 10x 1 50° 5 180° V 10x 5 180° 2 50° V 130° 5 13° V 10x 5 130° V x 5 _____ 10 Os dois ângulos medirão 6x 1 38° 5 6 ? 13 1 38° 5 116°; 4x 1 12° 5 4 ? 13° 1 12° 5 64° Os ângulos obtusos formados pelas retas medem 116° 11 O suplemento de um ângulo é igual à sua quinta parte. Quanto mede esse ângulo? x Chamando o ângulo de x, seu suplemento será __ . 5 5x __ 900° x x _____ __ ___ V Assim, x 1 5 180° V 1 5 5 5 5 5 900° 5 150° V 5x 1 x 5 900° V 6x 5 900° V x 5 _____ 6 12 Determine, em seu caderno, o valor de dois ângulos suplementares cuja diferença seja igual a 104°. Chamando um dos ângulos de x, o outro será x 2 104°. Assim, x 1 x 2 104° 5 180° V 284° 5 V 2x 5 180° 1 104° V 2x 5 284° V x 5 _____ 2 5 142°; x 2 104° 5 142° 2 104° 5 38° Os ângulos medem 142° e 38° 13 A diferença entre um ângulo e seu complemento é 40°. Calcule o valor desse ângulo. Chamando o ângulo de x, seu complemento será 90° 2 x. Assim, x 2 (90° 2 x) 5 40° V V x 1 x 2 90° 5 40° V 2x 5 90° 1 40° V 130° 5 65° V 2x 5 130° V x 5 _____ 2 14 A diferença entre um ângulo e seu suplemento é igual a 120°. Determine em seu caderno o valor desse ângulo. Chamando o ângulo de x, seu suplemento será 180° 2 x. Assim, x 2 (180° 2 x) 5 120° V V x 1 x 2 180° 5 120° V 2x 5 180° 1 120° V 300° V 2x 5 300° V x 5 _____ 5 150° 2 51 3P_YY_M8_RA_C02_038a067.indd 51 20.10.08 10:59:34 resolução de atividades Capítulo 2 15 O suplemento de um ângulo excede em 10° o triplo do seu complemento. Qual é o valor desse ângulo? O complemento de um ângulo x pode ser representado por 90° 2 x, e seu suplemento, por 180° 2 x. Assim, 180° 2 x 5 3 ? (90° 2 x) 1 10° V V 180° 2 x 2 10° 5 3 ? (90° 2 x) V V 170° 2 x 5 270° 2 3x V 2x 1 3x 5 270° 2 170° V 100° V 2x 5 100° V x 5 _____ 5 50° 2 16 Duas retas paralelas, interceptadas por uma transversal, determinam ângulos alternos cujas medidas são expressas por 10x 2 1° e 6x 1 15°. Calcule em seu caderno a medida de um dos ângulos obtusos determinados por essas retas. Os dois ângulos são alternos, portanto são congruentes. Assim, 10x 2 1° 5 6x 115° V 16° V 10x 2 6x 5 15° 1 1° V 4x 5 16° V x 5 ___ 5 4°. 4 Assim, os ângulos medem 10 ? 4° 2 1° 5 5 40° 2 1° 5 39°. Como se quer encontrar os ângulos obtusos formados pelas retas, tem–se que 180° 2 39°5 141°. 17 Os pares de lados opostos dos quadriláteros abaixo estão contidos em retas paralelas. Por isso eles são chamados de paralelogramos. Determine, em seu caderno, os valores de x, y e z nos paralelogramos a seguir. a) z x y 40° Os ângulos x e 40° são colaterais internos, ou seja, são suplementares. Assim, x 1 40° 5 180° V V x 5 180° 2 40° V x 5 140°. Os ângulos y e 40° são colaterais internos, ou seja, são suplementares. Assim, y 1 40° 5 180° V V y 5 180° 2 40° V y 5 140°. Os ângulos z e x são colaterais internos, ou seja, são suplementares. Assim, z 1 x 5 180° V z 1 140° 5 5 180° V z 5 180° 2 140° V z 5 40°; x 5 y 5 140°, z 5 40° b) y x z 74° Os ângulos z e 74° são alternos internos, ou seja, são congruentes. Assim, z 5 74°. Os ângulos z e y são colaterais internos, ou seja, são suplementares. Assim, y 1 z 5 180° V V y 1 74° 5 180° V y 5 180° 2 74° V y 5 106°. Os ângulos y e x são colaterais internos, ou seja, são suplementares. Assim, y 1 x 5 180° V V x 1 106° 5 180° V x 5 180° 2 106° V x 5 74°; z 5 x 5 74°, y 5 106°. c) z x � 30° y x Os ângulos x 1 30° e x são colaterais internos, ou seja, são suplementares. Assim, x 1 30° 1 x 5 180° V V 2x 5 180° 2 30° V 2x 5 150° V 150° 5 75° V x 5 _____ 2 Os ângulos x e y são colaterais internos, ou seja, são suplementares. Assim, y 1 x 5 180° V y 1 75° 5 180° V y 5 180° 2 75° V V y 5 105° Os ângulos z e y são colaterais internos, ou seja, são suplementares. Assim, z 1 y 5 180° V z 1 105° 5 180° V z 5 180° 2 105° V V z 5 75°; x 5 z 5 75°, y 5 105° d) y x z x � 90° Os ângulos x 2 90° e x são colaterais internos, ou seja, são suplementares. Assim, x 2 90° 1 x 5 180° V V 2x 5 180° 1 90° V 2x 5 270° V 270° V x 5 _____ 5 135° 2 Os ângulos x e y são colaterais internos, ou seja, são suplementares. Assim, y 1 x 5 180° V V y 1 135° 5 180° V y 5 180° 2 135° V y 5 45°. Os ângulos z e y são colaterais internos, ou seja, são suplementares. Assim, z 1 y 5 180° V V z 1 45° 5 180° V z 5 180° 2 45° V z 5 135°; x 5 z 5 135°, y 5 45° 18 Uma transversal determina, com duas retas paralelas, ângulos colaterais cujas medidas são expressas por 4x 1 16° e x 1 14°. Calcule, em seu caderno, a medida de um dos ângulos agudos determinados por essas retas. Os dois ângulos são colaterais, portanto são suplementares. Assim, 4x 1 16° 1 x 1 14° 5 180° V V 5x 1 30° 5 180° V 5x 5 180° 2 30° V 150° V 5x 5 150° V x 5 _____ 5 30° 5 Os ângulos medirão 4x 1 16° 5 4 ? 30° 1 16° 5 5 120° 1 16° 5 136°; x 1 14° 5 30° 1 14° 5 44° O ângulo agudo mede 44°. Página 59 Atividades para casa 19 Na figura a seguir, as retas r e s são paralelas. Determine em seu caderno o valor de 3x 2 y. r 110° x s 30° y 52 4P_YY_M8_RA_C02_038a067.indd 52 29.10.08 14:40:14 resolução de atividades Capítulo 2 Pela figura, pode–se ver que 30° 1 x 5 110° (alternos internos) V x 5 110° 2 30° V x 5 80°. Mas x 5 y, pois são opostos pelo vértice. Assim, y 5 80°. Deste modo, 3x 2 y 5 3 ? 80° 2 80° 5 240° 2 80° 5 5 160°. b)Traça–se outra reta, paralela a r e s, e nomeia–se um dos ângulos da nova figura. r 133° s 23° 20 Determine em seu caderno o valor do ângulo a da figura abaixo, sabendo que as retas r e s são paralelas. O ângulo formado pela soma de a e 23° é colateral interno do ângulo de 133°. Assim, a 1 23° 1 133° 5 180° V a 1 156° 5 180° V V a 5 180° 2 156° V a 5 24°. Os ângulos x e a são colaterais internos, logo a sua soma é 180°. x 1 a 5 180° V x 1 24° 5 180° V V x 5 180° 2 24° V x 5 156° r 3x 2x a s x � 130° A soma dos ângulos 2x e 3x é correspondente ao ângulo de 130°. Assim, 2x 1 3x 5 130° V 5x 5 130° 5 26° 5 130° V x 5 _____ 5 Como o ângulo buscado é suplementar ao ângulo 3x, 180° 2 3x 5 a V a 5 180° 2 78° 5 102° 21 Duas retas paralelas concorrem com uma transversal de modo que o triplo do ângulo agudo formado, somado com a quarta parte do ângulo obtuso, resulta em 177°. Calcule em seu caderno a medida do ângulo agudo formado por essas retas. Chamando de x o ângulo agudo e y o ângulo obtuso, y tem–se 3x 1 __ 5 177°. Sabe–se que x 1 y 5 180° V 4 V x 5 180° 2 y. Substituindo x por 180° 2 y na priy meira relação & 3 ? (180° 2 y) 1 __ 5 177° V 4 (180° 2 y) __ y 708° V 12 ? __________ V 1 5 _____ 4 4 4 V 12 ? (180° 2 y) 1 y 5 708° V 2 160° 2 12y 1 y 5 5 708° V 211y 5 708° 2 2 160° V (21) ? (211y) 5 1 452 5 (21 452) ? (21) V 11y 5 1 452 V y 5 _____ 5 132° 11 O ângulo agudo será x 5 180° 2 y V x 5 180° 2 132 V V x 5 48° 22 Sendo r e s retas paralelas, determine, em seu caderno, o valor de cada incógnita. a)Traça–se outra reta, paralela a r e s, e nomeia–se um dos ângulos da nova figura. r c)Traçam–se duas outras retas, paralelas a r e s, e nomeiam–se dois dos ângulos da nova figura. r 50° s 160° 100° � �x O ângulo formado pela soma de a e 100° é alterno interno do ângulo de 160°. Assim, a 1 100° 5 60° V V a 5 160° 2 100° V a 5 60°. Os ângulos a e b são alternos internos e, portanto, a 5 b 5 60°. O ângulo formado pela soma de b e x é colateral interno do ângulo de 50°. Desse modo, tem–se que b 1 x 1 50° 5 180° V 60° 1 x 1 50° 5 180° V V x 1 110° 5 180° V x 5 180° 2 110° V x 5 70° 23 Calcule em seu caderno a medida do ângulo A O B, ___ sabendo que as retas r e s são paralelas, e que AO ___ e 0B são transversais. Traça–se outra reta, paralela a r e s, dividindo o ânO B em dois (a e b). gulo A A O 2x 1 6° a b 5x 1 16° x s s 12° t r 130° � Os ângulos a e 130° são colaterais internos e, portanto, são suplementares. Assim, a 1 130° 5 180° V V a 5 180° 2 130° V a 5 50°. O ângulo formado pela soma de a e 12° é alterno interno de x. Deste modo, a 1 12° 5 x V 50° 1 12° 5 5 x V x 5 62° B 118° 2 3x Os ângulos a e 2x 1 6° são correspondentes e, portanto, a 5 2x 1 6°. Os ângulos b e 118° 2 3x são correspondentes e, portanto, b 5 118° 2 3x. O B 5 a 1 b V Assim, tem–se que A V 5x 1 16° 5 2x 1 6° 1 118° 2 3x V V 5x 1 16° 5 2x 1 124° V 5x 1 x 5 124° 2 16° V 180° V 6x 5 108° V x 5 _____ 5 18° 6 53 4P_YY_M8_RA_C02_038a067.indd 53 29.10.08 14:40:18 resolução de atividades Capítulo 2 B 5 5x 1 16° V A Desse modo, A O O B 5 5 ? 18° 1 16° V B V A O B 5 90° 1 16° V A O 5 106°. 24 Calcule em seu caderno o valor de cada incógnita, sabendo que as retas r e s são paralelas. Traçamos outra reta, paralela à reta t, e nomeamos um dos ângulos da nova figura. a 1 b 5 162° V a 1 84° 5 162° V a 5 162° 2 84° V V a 5 78° Os ângulos a e x são correspondentes, então x 5 78°. c)Traçamos outra reta, paralela a r e s, dividindo o ângulo x em dois (a e b). r r 80° s b a a 110° t 80° c d x b 170° s O outro ângulo interno do triângulo mede 80° (são opostos pelo vértice). Os ângulos d e 110° são suplementares, assim d 5 70°. Os ângulos a e d são correspondentes, assim a 5 d 5 70°. No triângulo tem-se: d 1 80° 1 c 5 180° V V 70° 1 80° 1 c 5 180° V 150° 1 c 5 180° V V c 5 180° 2 150° V c 5 30° A soma de a, b e c é igual a 180°, assim b 5 180° 2 30° 2 70 5 80°. Os ângulos medem a 5 70°; b 5 80°; c 5 30°; d 5 70°. Os ângulos a e 90° são correspondentes, então a 5 90°. Os ângulos b e 170° são colaterais internos, então b 5 10°. Deste modo tem–se que x 5 a 1 b V V x 5 90° 1 10° V x 5 100°. d)Traçamos outra reta, paralela a r e s, dividindo o ângulo de 90° em dois (a e b). r 180° 2 2x a 25 Calcule em seu caderno o valor de x, sabendo que as retas r e s são paralelas. a)Traçamos outra reta, paralela a r e s, dividindo o ângulo x em dois (a e b). 152° r 144° s x a b Os ângulos a e 152° são suplementares, assim a 5 28°. Os ângulos b e 144° são colaterais internos, então b 5 36°. Desse modo, tem–se que x 5 a 1 b V V x 5 28° 1 36° V x 5 64° b)Traçamos outra reta, paralela a r e s, dividindo o ângulo de 162° em dois (a e b). r x a 162° b s 96° Os ângulos b e 96° são colaterais internos, então b 5 84° b s 180° 2 3x Os ângulos a e 180° 2 2x são colaterais internos, então a 5 180° 2 (180° 2 2x) 5 5 180° 2 180° 1 2x 5 2x. Os ângulos b e 180° 2 3x são colaterais internos, então b 5 180° 2 (180° 2 3x) 5 180° 2 180° 1 3x 5 3x. Desse modo, tem–se que x 5 a 1 b V 90° 5 2x 1 3x V 90° V 90° 5 5x V ____ 5 x V x 5 18° 5 Módulo 4: Polígonos Página 61 Boxe Cálculo mental Se o número de diagonais d de um polígono conn . (n 2 3) , calcule vexo de n lados é dado por d 5 __________ 2 mentalmente o número de diagonais dos seguintes polígonos convexos: quadrilátero, pentágono, hexágono, heptágono e octógono. 4 . (4 2 3) 52 Quadrilátero & n 5 4 V d 5 __________ 2 5 . (5 2 3) 55 Pentágono & n 5 5 V d 5 __________ 2 6 . (6 2 3) 59 Hexágono & n 5 6 V d 5 __________ 2 7 . (7 2 3) 5 14 Heptágono & n 5 7 V d 5 __________ 2 8 . (8 2 3) 5 20 Octógono & n 5 8 V d 5 __________ 2 54 4P_YY_M8_RA_C02_038a067.indd 54 29.10.08 14:40:21 resolução de atividades Capítulo 2 Página 62 Atividades para classe b) 1 Calcule, em seu caderno, o número de diagonais dos seguintes polígonos. a) Undecágono 11 ? (11 2 3) _____ 11 ? 8 ___ 88 D 5 __________ 5 5 44 5 2 2 2 b) Eneágono 9 ? (9 23) _____ 9 ? 6 ___ 54 5 5 27 5 D 5 __________ 2 2 2 4,1 4,1 4,1 4,1 4,1 P 5 6 ? 4,1 5 24,6 c) 1,8 0,4 0,8 0,4 2,1 2,6 P 5 1,8 1 0,4 1 0,4 1 0,4 1 2,6 1 2,1 1 0,8 1 1 0,9 5 9,4 d) 2 Qual é a quantidade máxima de diagonais que podem ser traçadas a partir de um único vértice de um polígono convexo de 15 lados? O número de diagonais que sai de cada vértice é representado por n 2 3. Assim, n 2 3 5 15 2 3 5 12. 3 É possível traçar, de cada vértice de um polígono convexo, um número máximo de 28 diagonais. Quantos lados tem esse polígono? O número de diagonais que sai de cada vértice é representado por n 2 3. Assim, se o número de diagonais que sai de cada vértice é 28, tem–se que n 2 3 5 28 V n 5 28 1 3 5 31. Esse polígono tem 31 lados. 0,4 0,9 c) Decágono 10 ? (10 2 3) _____ 10 ? 7 ___ 70 5 5 35 5 D 5 ___________ 2 2 2 d)Dodecágono 12 ? (12 2 3) _____ 12 ? 9 ____ 108 5 5 54 5 D 5 ___________ 2 2 2 4,1 4,5 3,2 2,6 4,9 P 5 4,5 1 3,2 1 4,9 1 2,6 5 15,2 e) 0,6 2,3 1,1 1,3 0,8 1,9 2,6 P 5 2,3 1 0,6 1 1,1 1 0,8 1 2,6 1 1,9 1 1,3 5 10,6 4 Um quiliógono é um polígono de 1 000 lados. Quantas diagonais tem um quiliógono? 1 000 ? (1 000 2 3) 1 000 ? 997 997 000 5 __________ 5 ________ 5 D 5 _________________ 2 2 2 5 498 500 5 Quantas diagonais um icoságono tem a mais que um decágono? Número de diagonais do icoságono & 20 ? (20 2 3) _______ 20 ? 17 ____ 340 5 5 5 170 & D 5 ____________ 2 2 2 Número de diagonais do decágono & 10 ? (10 2 3) _____ 10 ? 7 ___ 70 5 & D 5 ___________ 5 5 35 2 2 2 A diferença entre as diagonais dos dois polígonos é 170 2 35 5 135 diagonais. 6 Calcule o perímetro dos polígonos a seguir 2,7 a) 0,8 3 2,5 3 P 5 2,7 1 3 1 3 1 2,5 1 0,8 5 12 f) 2,5 2,5 2,5 2,5 2,5 P 5 5 ? 2,5 5 12,5 7 A quantidade de diagonais de certo polígono que parte de um único vértice é 27. a) Qual é a quantidade de vértices desse polígono? O número de diagonais que sai de cada vértice é representado por n 2 3. Assim, se o número de diagonais que sai de cada vértice é 27, tem–se que n 2 3 5 27 V n 5 27 1 3 5 30. Esse polígono tem 30 vértices. b) Quantos lados possui esse polígono? O número de vértices e lados de um polígono é igual, então se o polígono tem 30 vértices ele terá 30 lados. c) Qual é a quantidade total de diagonais que esse polígono tem? 30 ? (30 2 3) _______ 30 ? 27 ____ 810 5 5 5 405 diagonais D 5 ____________ 2 2 2 55 3P_YY_M8_RA_C02_038a067.indd 55 20.10.08 10:59:36 resolução de atividades Capítulo 2 8 Se de cada vértice de um polígono convexo partem 12 diagonais, quantas diagonais ele tem? O número de diagonais que sai de cada vértice é representado por n 2 3. Assim, se o número de diagonais que sai de cada vértice é 12, tem–se que n 2 3 5 12 V n 5 12 1 3 5 15. Esse polígono tem 15 lados. Assim, o total de diago15 ? (15 2 3) ______ 15 ? 12 ____ 180 5 5 90. nais será D 5 ___________ 5 2 2 2 9 Qual é o nome do polígono que não tem diagonais? Se o polígono não tem diagonais, então D 5 0. n ? (n 2 3) n ? (n 2 3) V 0 5 __________ V 2 ? 0 5 D 5 __________ 2 2 5 n ? (n 2 3) V n ? (n 2 3) 5 0 V n 5 0 ou n 5 3 n 5 3 & o polígono que tem três lados denomina–se triângulo. 10 Qual polígono tem o número de lados igual ao número de diagonais? Se o número de lados é igual ao número de diagonais, então D 5 n. n ? (n 2 3) 2n V ___ n 5 n 2 3 V 2 5 n 2 3 V n 5 5 n 5 __________ 2 O polígono que tem cinco lados denomina–se pentágono. 11 Qual polígono tem o número de diagonais igual ao quádruplo do número de lados? Se o número de diagonais é igual ao quádruplo do número de lados, então D 5 4n. n ? (n 2 3) V 2 ? 4n 5 n ? (n 2 3) V 8n 5 4n 5 __________ 2 2 2 5 n 2 3n V n 2 3n 2 8n 5 0 V n2 2 11n 5 0 V V n ? (n 2 11) 5 0 V n 5 0 ou n 5 11 O polígono que tem 11 lados denomina–se undecágono. 12 Juliano pretende cercar com arame farpado um terreno com o formato e as medidas indicadas na figura a seguir. 14,8 m 6,2 m 6,4 m 7,8 m responda: quantas diagonais tem o polígono convexo cujos vértices são os pontos de intersecção das retas com a circunferência? C B O C A B D O A D O polígono construído tem oito lados. Assim o número de diagonais será 8 ? (8 2 3) _____ 8 ? 5 ___ 40 5 5 20. D 5 __________ 5 2 2 2 14 Numa festa estavam 14 pessoas, e cada uma cumprimentou as demais com apenas um aperto de mão. Quantos apertos de mão foram dados? Considerando um polígono de 14 lados, em cada vértice representa uma pessoa da festa, cada aperto de mão corresponde a um lado ou uma diagonal desse polígono. Dessa forma, o número total de apertos de mão corresponde à soma do número de lados com o número de diagonais do polígono de 14 lados. O n . (n 2 3) ______ 14 ? 11 número de diagonais é __________ 5 5 77. 2 2 Logo o número de apertos de mão é 77 1 14 5 91. Página 63 Atividades para casa 15 Se de cada vértice de um polígono partem 30 diagonais, quantos lados ele tem? O número de diagonais que sai de cada vértice é representado por n 2 3. Assim, se o número de diagonais que sai de cada vértice é 30, tem–se que n 2 3 5 30 V n 5 30 1 3 5 33. 16 Quantas diagonais partem de cada vértice de um polígono de 18 lados? O número de diagonais que sai de cada vértice é representado por n 2 3. Assim, se o número de lados é 18, tem–se que n 2 3 5 18 2 3 5 15. 12,7 m Sabendo que ele irá passar quatro voltas de arame em torno do terreno, calcule quantos metros Juliano precisa comprar. Juliano irá passar 4 voltas de arame em volta do terreno, assim terá de comprar 4 vezes a medida de seu perímetro. Assim, 4P 5 4 ? (14,8 1 6,4 1 7,8 1 12,7 1 6,2) V V 4P 5 4 ? 47,9 V 4P 5 191,6 m. Ele terá de comprar 191,6 m de arame. 13 Desenhe uma circunferência de centro O e raio 4___ cm em seu caderno e a seguir desenhe um diâmetro AB . ___ Depois, desenhe um diâmetro CD , perpendicular ___ a AB , e trace as bissetrizes dos ângulos formados por esses diâmetros. Observando essa figura, 17 Calcule o número de diagonais dos seguintes polígonos. a) Pentadecágono 15 ? (15 2 3) ______ 15 ? 12 ____ 180 5 5 5 90 D 5 ___________ 2 2 2 b) Hexadecágono 16 ? (16 2 3) ______ 16 ? 13 ____ 208 5 D 5 ___________ 5 5 104 2 2 2 c) Icoságono 20 ? (20 2 3) _______ 20 ? 17 ____ 340 D 5 ____________ 5 5 5 170 2 2 2 d)Tridecágono 13 ? (13 2 3) ______ 13 ? 10 ____ 130 D 5 ___________ 5 5 5 65 2 2 2 56 4P_YY_M8_RA_C02_038a067.indd 56 29.10.08 14:40:55 resolução de atividades Capítulo 2 18 Calcule o perímetro de cada um dos polígonos a seguir. 3,2 a) 3,2 3,2 3,2 3,2 3,2 3,2 3,2 P 5 8 ? 3,2 5 25,6 b) 4,7 2,3 2,3 4,7 P 5 4,7 1 2,3 1 4,7 1 2,3 5 14 c) 2,8 1,2 5,8 1,7 22 Lucas contou a Paulo que tinha ido a uma festa. Paulo perguntou quantas pessoas havia na festa. Então Lucas disse: “Quantas pessoas havia, eu não sei, mas sei que cada uma das pessoas presentes à festa cumprimentou cada uma das outras com um único aperto de mão, e sei que foram dados 45 apertos de mão”. Paulo fez algumas contas e descobriu o número de pessoas na festa. Quantas eram essas pessoas? Imaginando cada pessoa como o vértice de um polígono, cada aperto de mão corresponde a um lado ou uma diagonal do polígono. Assim, sendo n o número de pessoas na festa, o número de apertos de mão corresponde à soma do número de lados e do número de diagonais de um polígono de n lados. n . (n 2 3) n . (n 2 3) n 1 __________ 5 45 V n 1 __________ 5 2 2 2 . (n 2 1) n 2n 1 n 2 3n _________ 5 ____________ 5 5 45 V n . (n 2 1) 5 90. 2 2 Assim, a quantidade de pessoas na festa é um número que, multiplicado por seu antecessor, resulta em 90. Por investigação, esse número é 10, pois 10 ? 9 5 90. Portanto, havia dez pessoas na festa. 23 Copie e complete a tabela abaixo em seu caderno. 4,6 P 5 2,8 1 5,8 1 4,6 1 1,7 1 1,2 5 18,9 2,6 d) 2,3 3,3 1,8 2,5 2,5 P 5 2,6 1 2,3 1 1,8 1 2,5 1 2,5 1 3,3 5 15 19 Um triacontágono é um polígono com 30 lados. Quantas diagonais tem um triacontágono? 30 ? (30 2 3) _______ 30 ? 27 ____ 810 5 5 5 405 D 5 ____________ 2 2 2 20 Se de cada vértice de um polígono convexo partem 20 diagonais, quantas diagonais esse polígono tem? O número de diagonais que sai de cada vértice é representado por n 2 3. Assim, se o número de diagonais que sai de cada vértice é 20, tem–se que n 2 3 5 20 V n 5 20 1 3 5 23 Assim, o número de diagonais é 23 ? (23 2 3) _______ 23 ? 20 ____ 460 5 D 5 ____________ 5 5 230 2 2 2 21 Qual polígono tem número de lados igual a dois terços do número de diagonais? Se o número de lados do polígono é igual a dois 2 terços do número de diagonais, então __ D 5 n, ou 3 3 D 5 __ n. 2 n ? (n 2 3) 3 V 2 ? 3n 5 2n ? (n 2 3) V Assim, __ n 5 __________ 2 2 2 2 V 6n 5 2n 2 6n V 2n 2 6n 2 6n 5 0 V V 2n2 2 12n 5 0 V 2n ? (n 2 6) 5 0 V 2n 5 0 V V n 5 0 ou n 2 6 5 0 V n 5 6 O polígono que tem seis lados denomina–se hexágono. Número de lados do polígono Número de diagonais do polígono 4 lados 2 diagonais 5 lados 5 diagonais 6 lados 9 diagonais 7 lados 14 diagonais 8 lados 20 diagonais n ? (n 2 3) __________ 2 (n 1 2) ? (n 2 1) _______________ 2 (n 2 5) ? (n 2 8) _______________ 2 n lados (n 1 2) lados (n 2 5) lados 24 a) Em um polígono convexo, a quantidade de diagonais é igual ao triplo da quantidade de lados. Qual é esse polígono? A quantidade de diagonais é o triplo da quantidade de lados & D 5 3n (n 2 3) ___ n . (n 2 3) 3n V _______ 5 n 5 3 V n 2 3 5 3n 5 __________ 2 2 56Vn59 O polígono convexo que tem 9 lados é o eneágono. b) Qual é o polígono convexo em que a quantidade de diagonais é igual a seis vezes a quantidade de lados? A quantidade de diagonais é o sêxtuplo da quantidade de lados & D 5 6n (n 2 3) ___ n . (n 2 3) 6n V _______ 5 n 5 6 V n 2 3 5 6n 5 __________ 2 2 5 12 V n 5 15 O polígono convexo que tem 15 lados é o pentadecágono. Observação: Em ambos os itens foi feita uma divisão por n, o que é possível, visto que se n representa o número de lados de um polígono, ele é diferente de zero. 57 4P_YY_M8_RA_C02_038a067.indd 57 29.10.08 14:40:58 resolução de atividades Capítulo 2 25 Um polígono tem cinco lados a mais que outro. Determine que polígonos são esses, sabendo que a diferença entre o total de diagonais deles é igual a 40. Se um dos polígonos tem n lados, o outro tem (n 1 5) lados. Assim o número de diagonais é n ? (n 2 3) _______ n2 2 3n • para n lados & __________ 5 2 2 (n 1 5) ? (n 1 2) •para (n 1 5) lados & _______________ 5 2 n2 1 7n 1 10 ____________ 5 2 A diferença entre eles será n ? (n 2 3) (n 1 5) ? (n 1 2) __________ _______________ 2 5 40 2 2 2 2 n 1 7n 1 10 2 (n 2 3n) ___ 80 5 V V _______________________ 2 2 V n2 1 7n 1 10 2 n2 1 3n 5 80 V 10n 1 10 5 5 80 V 10n 5 80 2 10 V 10n 5 70 V n 5 7. Logo um polígono tem 7 lados, e o outro, 12 lados. Desse modo eles são chamados heptágono e dodecágono. 26 A soma do número de lados de dois polígonos é igual a 36 e a diferença entre as quantidades de diagonais desses dois polígonos é igual a 66. Dentre esses dois, quantas diagonais tem o polígono com o menor número de lados? Se chamarmos o número de lados de um dos polígonos de n, o número de lados do outro será (36 2 n). Assim o número de diagonais para o polígono de n n ? (n 2 3) _______ n2 2 3n lados será __________ 5 . 2 2 Para o polígono de (36 2 n) lados & (36 2 n) ? (33 2 n) 1 188 2 69n 1 n2 & _________________ 5 _______________ 2 2 A diferença entre eles será 1 188 2 69n 1 n2 _______ n2 2 3n _______________ 2 5 66 V 2 2 1 188 2 69n 1 n2 2 (n2 2 3n) ____ 132 __________________________ V 5 V 2 2 V 1 188 2 69n 1 n2 2 n2 1 3n 5 132 V V 266n 5 132 2 1 188 V (21) ? (266n) 5 1 056 5 16 5 21 056 ? (21) V 66n 5 1 056 V n 5 _____ 66 Então um dos polígonos tem 16 lados e o outro tem 36 2 16 5 20 lados, de modo que o primeiro tem um número menor de lados. Assim o número de diagonais deste polígono será 16 ? (16 2 3) ______ 16 ? 13 ____ 108 5 D 5 ___________ 5 5 104 2 2 2 Módulo 5: Ângulos de um polígono Página 65 Boxe Desafio A figura abaixo mostra parte de um polígono regular ___ ABCDE..., onde a reta r é perpendicular ao lado AB e a reta s é bissetriz do ângulo C D E. r A B s C O ângulo de 50° corresponde a 2 lados e meio, assim o ângulo correspondente a cada lado é de 20°. Para encontrar o número de lados faz–se 360° 360° _____ 5 n 5 _____ a 5 18 lados. 20° Página 66 Atividades para classe 1 Determine a soma dos ângulos internos dos seguintes polígonos. a) Octógono Si 5 (8 2 2) ? 180° 5 6 ? 180° 5 1 080° b) Decágono Si 5 (10 2 2) ? 180° 5 8 ? 180° 5 1 440° c) Pentadecágono Si 5 (15 2 2) ? 180° 5 13 ? 180° 5 2 340° d)Icoságono Si 5 (20 2 2) ? 180° 5 18 ? 180° 5 3 240° 2 Determine a soma dos ângulos externos dos seguintes polígonos. a) Pentadecágono c) Quiliógono b) Icoságono d)Eneágono A soma dos ângulos externos de qualquer polígono é sempre 360°. 3 Calcule a soma dos ângulos internos, a soma dos ângulo externos e o número de diagonais de um polígono de 24 lados. • Si 5 (24 2 2) ? 180° 5 22 ? 180° 5 3 960° • Se 5 360° 24 ? (24 2 3) ______ 504 24 ? 21 ____ 5 • D 5 ____________ 5 5 252 2 2 2 4 Determine o ângulo desconhecido dos seguintes polígonos. a) 120° x 100° 130° 100° Soma dos ângulos internos de um pentágono & & Si 5 (5 2 2) ? 180° 5 3 ? 180° 5 540°. Dessa forma, tem-se: x 1 120° 1 100° 1 130° 1 100° 5 540° V V x 1 450° 5 540° V x 5 540° 2 450° V V x 5 90° b) 120° x 130° 160° D E 50° Calcular o número de lados desse polígono. x � 60° 150° Soma dos ângulos internos de um hexágono & & Si 5 (6 2 2) ? 180° 5 4 ? 180° 5 720°. 58 3P_YY_M8_RA_C02_038a067.indd 58 20.10.08 10:59:37 resolução de atividades Capítulo 2 Dessa forma, tem-se: x 1 120° 1 130° 1 160° 1 x 1 60° 1 150° 5 720° V V 2x 1 620° 5 720° V 100° V 2x 5 720° 2 620° V 2x 5 100° V x 5 _____ 5 50° 2 O valor do ângulo representado por x 1 60° será x 1 60° 5 50° 1 60° 5 110°. c) 100° 170° 120° 6 Nos itens abaixo você visualiza partes de polígonos regulares, com os ângulos externos assinalados. Determine a medida do ângulo interno em cada caso. A soma do ângulo interno de um polígono com seu ângulo externo é sempre 180°. Assim, a) 130° x A soma dos ângulos internos de um pentágono é igual a 540°. Assim, 120° 1 100° 1 150° 1 130° 1 (180° 2 x) 5 540° V V 500° 1 180° 2 x 5 540° V 680° 2 x 5 540° V V 680° 2 540° 5 x V x 5 140° 140° 36° Soma dos ângulos internos de um heptágono & & Si 5 (7 2 2) ? 180° 5 5 ? 180° 5 900°. Dessa forma tem-se: x 1 90° 1 170° 1 100° 1 120° 1 130° 1 140° 5 5 900° V x 1 750° 5 900° V x 5 900° 2 750° V V x 5 150° ai 5 180° 2 36° 5 144° 5 Determine o valor de x nos seguintes casos. O exercício não fornece todos os ângulos internos dos polígonos, mas mostra as medidas dos ângulos externos & ai 5 180° 2 ae ai 5 180° 2 30° 5 150° a) 52° 3x � 20° 48° A soma dos ângulos internos de um triângulo é igual a 180°. Assim, 48° 1 52° 1 [180° 2 (3x 2 20°)] 5 180° V V 48° 1 52° 1 180° 2 3x 1 20° 5 180° V V 300° 2 3x 5 180° V 23x 5 180° 2 300° V 120° V 3x 5 120° V x 5 _____ 5 40° 3 b) x 112° 50° 78° A soma dos ângulos internos de um quadrilátero é igual a 360°. Assim, 78° 1 (180° 2 112°) 1 (180° 2 50°) 1 1 (180° 2 x) 5 360° V 78° 1 68° 1 130° 1 1 180° 2 x 5 360° V 456° 2 x 5 360° V V 456° 2 360° 5 x V x 5 96° c) 150° x 100° 24° ai 5 180° 2 24° 5 156° c) 30° 7 Os valores abaixo expressam medidas de ângulos internos de polígonos regulares. Para cada item, dê a medida do ângulo externo correspondente. A soma do ângulo interno de um polígono com seu ângulo externo é sempre 180°. Assim, a) 140° ae 5 180° 2 140° 5 40° b) 120° ae 5 180° 2 120° 5 60° c) 160° ae 5 180° 2 160° 5 20° d)165° ae 5 180° 2 165° 5 15° 8 Um polígono tem 4 320° como soma dos ângulos internos. Quantos lados tem esse polígono? Si 5 (n 2 2) ? 180° V 4 320° 5 (n 2 2) ? 180° V 4 320° 5 (n 2 2) V 24 5 n 2 2 V n 5 26 V _______ 180° 9 A soma dos ângulos internos de um polígono é 2 520°. Quantas diagonais ele tem? Para determinar o número de diagonais calcula–se o número de lados do polígono. Si 5 (n 2 2) ? 180° V 2 520° 5 (n 2 2) ? 180° V 2 520° 5 (n 2 2) V 14 5 n 2 2 V n 5 16 V _______ 180° Determinando o número de diagonais & 16 ? (16 2 3) ______ 16 ? 13 ____ 208 & D 5 ___________ 5 5 5 104 2 2 2 10 Em cada item abaixo é dado o ângulo externo de um polígono regular. Determine o número de lados de cada um deles. 130° 120° b) a) e 5 12° 360° 360° 12° 5 _____ V 12n 5 360 V n 5 _____ 5 30 n 12° 59 3P_YY_M8_RA_C02_038a067.indd 59 20.10.08 10:59:38 resolução de atividades Capítulo 2 b) e 5 15° 360° 360° V 15n 5 360 V n 5 _____ 5 24 15° 5 _____ n 15° c) e 5 20° 360° 360° V 20n 5 360 V n 5 _____ 5 18 20° 5 _____ n 20 d)e 5 45° 360° 360° V 45n 5 360 V n 5 _____ 58 45° 5 _____ n 45° 11 Em cada item abaixo há o valor do ângulo interno de um polígono regular. Calcule o número de lados de cada um desses polígonos. a) 150° Primeiramente, determina–se a medida do ângulo externo & ae 5 180° 2 150° 5 30°. Em seguida, determina–se o número de lados do 360° V 30n 5 360° V polígono & 30° 5 _____ n 360° V n 5 _____ 5 12 30° b) 144° 360° V 36°n 5 360° V ae 5 180° 2 144° 5 36° V 36° 5 _____ n 360° _____ 5 10 V n 5 36° c) 140° 360° V 40°n 5 360° V ae5 180° 2 140° 5 40° V 40° 5 _____ n 360° 59 V n 5 _____ 40° d)160° 360° V 20°n 5 360° V ae 5 180° 2 160° 5 20° V 20° 5 _____ n 360° V n 5 _____ 5 18 20° 12 Determine o número de diagonais de um polígono convexo cuja soma dos ângulos internos é igual a 3 960°. Para determinar o número de diagonais calcula–se o número de lados do polígono. 3 960° Si 5 (n 2 2) ? 180° V _______ 5 (n 2 2) V 22 5 180° 5 n 2 2 V n 5 24 Determinando o número de diagonais 24 ? (24 2 3) ______ 504 24 ? 21 ____ 5 5 5 252 D 5 ____________ 2 2 2 13 Determine o número de diagonais de um polígono regular cujo ângulo externo é 24°. Para determinar o número de diagonais calcula–se o número de lados do polígono. 360° 360° 24° 5 _____ 5 15 V 24n 5 360° V n 5 _____ n 24° Determinando o número de diagonais 15 ? (15 2 3) ______ 15 ? 12 ____ 180 5 5 5 90 D 5 ___________ 2 2 2 14 A figura abaixo mostra ___ parte ___ de um polígono regular ABCDE..., em que OA e OC são bissetrizes dos ângulos internos. Quantas diagonais tem esse polígono? B A C 0 ___ ___ Se OA e OC são bissetrizes dos ângulos internos, enBC A A B 5 O C B 5 ____ tão O . 2 e O C B de x e A BC de 2x, a soma Chamando O AB dos ângulos internos do quadrilátero ABCO é x 1 x 1 2x 1 90° 5 360° V 4x 5 360° 2 90° V 270° 5 67,5°; V 4x 5 270° V x 5 _____ 4 5 2 ? 67,5° 5 135°. A BC Se o ângulo interno do polígono mede 135°, seu ângulo externo mede 45°. Assim, o número de lados 360° 360° desse polígono será ae 5 _____ V 45° 5 _____ V n n 360° V 45°n 5 360° V n 5 _____ 5 8. 45° Determinando o número de diagonais 8 ? (8 2 3) _____ 8 ? 5 ___ 40 5 5 20 5 D 5 __________ 2 2 2 Página 67 Atividades para casa 15 Determine a soma dos ângulos internos dos seguintes polígonos. a) Heptágono Si 5 (7 2 2) ? 180° V Si 5 5 ? 180° V Si 5 900° b) Undecágono Si 5 (11 2 2) ? 180° V Si 5 9 ? 180° V Si 5 1 620° c) Tridecágono Si 5 (13 2 2) ? 180° V Si 5 11 ? 180° V Si 5 1 980° d)Hexadecágono Si 5 (16 2 2) ? 180° V Si 5 14 ? 180° V Si 5 2 520° 16 Determine quantos lados tem o polígono regular cujo ângulo externo é igual a 24°. 360° 360° 24° 5 _____ 5 15 V n 5 _____ n 24° 17 Calcule a medida do ângulo interno de um polígono regular de 30 lados. Primeiramente, determina–se o valor do ângulo 360° externo & ae 5 _____ V ae 5 12°. 30 Em seguida determina–se o valor do ângulo interno. ai 5 180° 2 12° V ai 5 168° 18 Calcule o número de diagonais de um polígono regular cujo ângulo externo mede 40°. Para determinar o número de diagonais calcula–se o número de lados do polígono. 360° 360° 59 40° 5 _____ V n 5 _____ n 40° Determinando o número de diagonais 9 ? (9 2 3) _____ 9 ? 6 ___ 54 5 D 5 __________ 5 5 27 2 2 2 19 Responda em seu caderno. a) Quanto mede o ângulo interno de um polígono regular cujo ângulo externo mede 20°? A soma do ângulo interno com o ângulo externo de um polígono é 180°. Assim, ai 5 180° 2 ae V V ai 5 180° 2 20° 5 160°. 60 3P_YY_M8_RA_C02_038a067.indd 60 20.10.08 10:59:38 resolução de atividades Capítulo 2 b) Quantos lados tem o polígono cuja soma dos ângulos internos é igual a 6 120°? Si 5 (n 2 2) ? 180° V 6 120° 5 (n 2 2) ? 180° V 6 120° V ______ 5 n 2 2 V 34 5 n 2 2 V n 5 36 180° c) Quantas diagonais tem o polígono regular cujo ângulo externo mede 12°? Para determinar o número de diagonais calcula–se o número de lados do polígono. 360° 360° V n 5 _____ 30 12° 5 _____ 5 n 12° Determinando o número de diagonais 30 ? (30 2 3) _______ 30 ? 27 ____ 810 405 5 5 5 D 5 ____________ 2 2 2 d)Quanto mede o ângulo externo de um polígono regular que tem 72 lados? 360° ae 5 _____ V ae 5 5° 72 e) Quanto mede o ângulo interno de um polígono que tem 40 lados? Primeiro determina–se o valor do ângulo externo do 360° V polígono & ae 5 _____ ae 5 9°. 40 Como a soma do ângulo externo com o ângulo interno é 180°, tem-se ai 5 180° 2 ae V V ai 5 180° 2 9° 5 171° 20 Calcule o valor de x nos seguintes casos. a) 100° 112° 126° 130° x Cálculo da soma dos ângulos internos do pentágono & Si 5 (5 2 2) ? 180° V Si 5 3 ? 180° V Si 5 540°. Assim, x 1 112° 1 100° 1 126° 1 130° 5 540° V V x 1 468° 5 540° V x 5 540° 2 468° V x 5 72° b) x�10° x�20° x x�40° x�20° x�30° Cálculo da soma dos ângulos internos do hexágono & Si 5 (6 2 2) ? 180° V Si 5 4 ? 180° V V Si 5 720°. Assim, x 1 x 1 10° 1 x 1 20° 1 x 1 40° 1 x 1 30° 1 x 1 20° 5 720° V 6x 1 120° 5 720° V 600° 5 V 6x 5 720° 2 120° V 6x 5 600° V x 5 _____ 6 5 100° b) A quantidade de lados de um polígono, sabendo que de cada um de seus vértices podem ser traçadas até 17 diagonais. O número de diagonais que sai de cada vértice de um polígono é dado por n 2 3. Assim, n 2 3 5 17 V V n 5 17 1 3 V n 5 20 lados. c) A quantidade de diagonais de um polígono, sabendo que de cada um de seus vértices saem 18 diagonais. Se de cada vértice do polígono são traçadas 18 diagonais, então o número de lados é 21. Assim, 21 ? (21 2 3) ______ 21 ? 18 ____ 378 189 diagonais. 5 5 5 D 5 ___________ 2 2 2 d)A medida do ângulo externo de um polígono regular, sabendo que de cada um de seus vértices partem 21 diagonais. Se de cada vértice do polígono são traçadas 21 diagonais, então o número de lados é 24. Assim, 360° 15°. 5 ae 5 _____ 24 22 Observe a moeda de RS || 0,25 na fotografia: a) Quantos lados possui o polígono representado nessa moeda? Sete lados. b) Se esse polígono é regular, qual é a medida aproximada do ângulo interno dele? Determinando a soma dos ângulos internos & Si 5 (n 2 2) ? 180° V Si 5 (7 2 2) ? 180° V V Si 5 5 ? 180° V Si 5 900°. Assim, o valor do ân900° 128,5°. gulo interno será ai 5 _____ 5 7 c) Qual é a medida aproximada do ângulo externo? ae 5 180° 2 ai V ae 5 180° 2 128,5° V ae 5 51,5° d)Determine o número de diagonais desse polígono. 7 ? (7 2 3) 28 7 ? 4 ___ 5 5 5 _____ 14 diagonais D 5 __________ 2 2 2 23 Calcule o número de diagonais de um polígono regular cujo ângulo interno mede 150°. Determinando o número de lados desse polígono & Se o ângulo interno mede 150°, então o ângulo ex360° V terno mede 30°. Assim, ae 5 _____ n 360° 360° _____ V 30°n 5 360° V n 5 _____ 5 V 30° 5 n 30° 5 12 lados. Dessa maneira, o número de diagonais será 12 ? (12 2 3) _____ 12 ? 9 ____ 108 5 5 5 D 5 ___________ 54 diagonais. 2 2 2 24 As diagonais do octógono regular abaixo foram pintadas conforme o tamanho: diagonais que têm o mesmo tamanho foram pintadas da mesma cor. 21 Determine em seu caderno. a) A quantidade máxima de diagonais que podem ser traçadas a partir de um vértice de um polígono de 32 lados. O número de diagonais que podem ser traçadas de cada vértice de um polígono é dado por n 2 3. Assim, 32 2 3 5 29 diagonais. 61 5P_YY_M8_RA_C02_038a067.indd 61 31.10.08 15:39:35 resolução de atividades Capítulo 2 Repare que foram usadas três cores. Indique no caderno quantas cores serão necessárias para executar o mesmo tipo de pintura das diagonais dos polígonos seguintes. Todas as diagonais são pintadas em pares, exceto a diagonal central que divide o polígono em duas partes iguais. a) Quadrado O quadrado possui duas diagonais congruentes. Assim, é necessária apenas uma cor. Tratamento da informação Construir e interpretar gráficos de setor circular 68 Página Matilde realizou uma pesquisa com 400 estudantes. Ela perguntou a eles por quantas horas diárias utilizavam a internet. A tabela abaixo mostra o resultado. Horas por dia b) Hexágono regular De cada vértice de um hexágono regular saem três diagonais. Tem-se assim um par de diagonais de mesmo tamanho e a diagonal central. Assim, são necessárias duas cores. c) Dodecágono regular De cada vértice de um dodecágono regular saem 9 diagonais, sendo 4 pares e a diagonal central. Assim, são necessárias 5 cores. 25 Calcule a soma das medidas dos cinco ângulos assinalados na figura abaixo. a e b c d Para resolver esse exercício devem–se nomear alguns ângulos da figura. a b g h i c e f j d Nos cinco triângulos maiores existentes na figura tem–se b 1 i 1 e 5 180°; a 1 j 1 c 5 180°; b 1 d 1 f 5 180°; a 1 h 1 d 5 180°; c 1 g 1 e 5 180°. Agora, devem–se somar as equações: b 1 i 1 e 1 a 1 j 1 c 1 b 1 d 1 f 1 a 1 h 1 d 1 c 1 g 1 e 5 5 5 ? (180°) V V (a 1 b 1 c 1 d 1 e) 1 (a 1 b 1 c 1 d 1 e) 1 1 (f 1 g 1 h 1 i 1 j) 5 900°. A soma dos ângulos (f 1 g 1 h 1 i 1 j) é 540°, por se tratar de um pentágono. Então, (a 1 b 1 c 1 d 1 e) 1 (a 1 b 1 c 1 d 1 e) 1 540° 5 900° V 2 ? (a 1 b 1 c 1 d 1 e) 5 360° V V a 1 b 1 c 1 d 1 e 5 180°. Coleta de informação 68 Página Número de pessoas Menos de 1 hora 80 2 horas 140 3 horas 100 4 horas 60 5 horas ou mais 20 Oraganização da informação Para divulgar os dados obtidos, Matilde quer utilizar um gráfico de setor circular. Para isso, é necessário calcular a porcentagem que cada resposta representa em relação ao número total de estudantes consultados. Copie a tabela abaixo em seu caderno e complete–a com as porcentagens correspondentes ao número de vezes que cada alternativa de resposta foi mencionada. Horas por dia Número de Pessoas Porcentagem Menos de 1 hora 80 20% 2 horas 140 35% 3 horas 100 25% 4 horas 60 15% 5 horas ou mais 20 5% Determinando as porcentagens: 140 140 • _____ ? 100% 5 ____ 35% 5 4 400 100 100 100% 5 ____ 25% 5 • _____ ? 4 400 60 60 100% 5 ___ 5 15% • _____ ? 4 400 20 20 100% 5 ___ 5 5% • _____ ? 4 400 Cada setor do gráfico de setor circular deve ser proporcional a uma das porcentagens obtidas na tabela acima. Assim, devemos dividir o arco total em partes proporcionais às porcentagens encontradas em cada caso. Consideramos então que um arco de 360° representa 100% dos estudantes e utilizamos uma regra de três simples para encontrar o arco correspondente à porcentagem dos estudantes que mencionou determinada resposta. Exemplo: 20% dos estudantes ficam menos de 1 hora utilizando a internet. 100% 360° x 20% Obtemos assim x 5 72°. 62 4P_YY_M8_RA_C02_038a067.indd 62 29.10.08 14:53:24 resolução de atividades Capítulo 2 Determina–se o ângulo de cada fatia do gráfico correspondente aos dados da pesquisa. • 20% dos estudantes ficam, em média, menos de 1 hora utilizando a internet. 100% 360° 20% x 7 200 V 100x 5 20 ? 360 V 100x 5 7 200 V x 5 ______ 100 V x 5 72° • 35% dos estudantes ficam, em média, 2 horas utilizando a internet. 360° 100% 35% x 12 600 100x 5 35 ? 360 V 100x 5 12 600 V x 5 ______ V 100 V x 5 126° • 25% dos estudantes ficam, em média, 3 horas utilizando a internet. 360° 100% 25% x 9 000 V 100x 5 25 ? 360 V 100x 5 9 000 V x 5 ______ 100 V x 5 90° • 1 5% dos estudantes ficam, em média, 4 horas utilizando a internet. 100% 360° 15% x 5 400 V 100x 5 15 ? 360 V 100x 5 5 400 V x 5 ______ 100 V x 5 54° • 5% dos estudantes ficam, em média, 5 horas ou mais utilizando a internet. 100% 360° 5% x 1 800 V 100x 5 5 ? 360 V 100x 5 1 800 V x 5 _____ 100 V x 5 18° Após calcular os ângulos correspondentes a cada setor, faça um círculo e divida–o de acordo com as medidas obtidas. Utilize o transferidor para marcar os ângulos. Depois, trace os segmentos que delimitam os setores e pinte cada um deles de uma cor diferente, para facilitar a visualização das informações obtidas. Dê um título ao gráfico e faça uma legenda. Horas gastas por dia na internet 5% 15% 25% Página 69 20% 35% menos de 1 hora 2 horas 3 horas 4 horas 5 horas ou mais Leitura de dados a) Existe algum setor circular formado por um arco de medida igual a um ângulo obtuso? Qual? Sim, a fatia correspondente a 35%. b) Existe algum setor que corresponda a um ângulo agudo? Qual? Sim, as fatias correspondentes às porcentagens de 5%, 15% e 20%. c) Existe algum setor que corresponda a um ângulo reto? Qual? Sim, a fatia correspondente a 25%. d)Vinte e cinco por cento correspondem a qual fração do arco do círculo? 25 1 25% 5 ____ 5 __ 100 4 Página 69 Comunicação de resultados Você fez um gráfico de setor circular para representar a situação estudada. Agora, represente os resultados dessa mesma pesquisa com um gráfico de barras. Horas gastas por dia na Internet 160 140 120 100 80 60 40 20 0 Página menos de 1 hora 69 2 horas 3 horas 4 horas 5 horas ou mais Faça você 1 Mônica reuniu–se com algumas amigas e saiu pela escola entrevistando alguns alunos e funcionários. Entre outras perguntas, elas pediam que as pessoas dissessem, dentre as frutas representadas abaixo, qual era a sua preferida. Abacate Abacaxi Banana Mamão Melancia A partir das respostas obtidas, elas montaram a tabela abaixo. Utilize as informações da tabela e monte um gráfico de setor circular. Frutas Quantidade de pessoas Abacate 166 Abacaxi 150 Banana 100 Mamão 50 Melancia 34 Determina–se a porcentagem que cada resposta representa em relação ao número total de pessoas entrevistadas. 63 3P_YY_M8_RA_C02_038a067.indd 63 20.10.08 10:59:39 resolução de atividades Capítulo 2 O número total de pessoas é 166 1 150 1 100 1 1 50 1 34 5 500. Então as porcentagens são 166 166 • ____ ? 100% 5 ____ 5 33,2% 5 500 150 150 5 30% • ____ ? 100% 5 ____ 5 500 100 100 5 20% • ____ ? 100% 5 ____ 5 500 50 • ____ ? 100% 5____ 50 5 10% 500 5 34 34 ____ ___ • ? 100% 5 5 6,8% 5 500 Frutas Quantidade de pessoas Porcentagem Abacate 166 33,2% Abacaxi 150 30,0% Banana 100 20,0% Mamão 50 10,0% Melancia 34 6,8% Em seguida determina–se o ângulo de cada fatia do gráfico correspondente aos dados da pesquisa. • 33,2% dos entrevistados preferem abacate. 360° 100% x 33,2% 11 952 5 100x 5 33,2 ? 360 V 100x V 11 952 V x 5 ______ 100 5 119,5° • 30% dos entrevistados preferem abacaxi. 360° 100% x 30% 10 800 5 100x 5 30 ? 360 V 100x 5 10 800 V x 5 _______ 100 5 108° • 20% dos entrevistados preferem banana. 360° 100% x 20% 7 200 5 100x 5 20 ? 360 V 100x 5 7 200 V x 5 ______ 100 5 72° • 10% dos entrevistados preferem mamão. 360° 100% x 10% 3 600 5 100x 5 10 ? 360 V 100x 5 3 600 V x 5 ______ 100 5 36° • 6,8% dos entrevistados preferem abacate. 360° 100% x 6,8% 2 448 100x 5 6,8 ? 360 V 100x 5 2 448 V x 5 ______ 100 24,5° 10% FRUTAS PREFERIDAS 6,8% 33,2% Abacate Abacaxi Banana Mamão Melancia 20% 30% 2 O gráfico abaixo mostra a distribuição das 30 medalhas que os alunos da escola Bom Futuro ganharam em um campeonato estadual. QUADRO DE MEDALHAS DA ESCOLA BOM FUTURO 30% Ouro Prata Bronze 50% 20% a) Analisando os dados do gráfico, encontre a quantidade de medalhas de ouro, de prata e de bronze que os alunos dessa escola ganharam. Medalhas de ouro & 30% de 30 5 0,3 ? 30 5 5 9 medalhas. Medalhas de prata & 20% de 30 5 0,2 ? 30 5 5 6 medalhas. Medalhas de bronze & 50% de 30 5 0,5 ? 30 5 5 15 medalhas. b)Qual é a medida, em graus, de cada arco indicado? • 30% das medalhas são de ouro. 360° 100% x 30% 10 800 5 100x 5 30 ? 360 V 100x 5 10 800 V x 5 _______ 100 5 108° • 20% das medalhas são de prata. 360° 100% x 20% 7 200 5 100x 5 20 ? 360 V 100x 5 7 200 V x 5 ______ 100 5 72° • 50% das medalhas são de bronze. 360° 100% x 50% 18 000 5 100x 5 50 ? 360 V 100x 5 18 000 V x 5 _______ 100 5 180° Página 72 Questões globais B C em cada caso indi 1 Calcule o valor do ângulo A cado abaixo. a) b) A A 31° 44’ 31° 24’ B 48° 30’ 22° 30’ 31° 24’ 1 22° 30’ 53° 54’ C B C 31° 44’ 1 48° 30’ 79° 74’ 1 1° 14’ 80° 14’ 64 4P_YY_M8_RA_C02_038a067.indd 64 29.10.08 14:58:43 resolução de atividades Capítulo 2 2 Antonieta é decoradora e recebeu a tarefa de decorar uma sala no formato abaixo. Para isso, ela precisa saber as medidas de todos os ângulos. Meça os ângulos com um transferidor e diga quais são agudos, obtusos ou retos. B C 154º 135º D A 101º 135º 90º 105º E F Agudo: nenhum. Obtusos: A, B, C, D, F. Reto: E. ___ 3 Sendo M o ponto médio de AB , calcule AB. A 18 � x M 16 � y B 5 Na figura abaixo, as retas r e s são paralelas. r A Determine a medida do 3x � 4° ângulo A O B. 0 a 2x � 4° Traçamos outra reta, pab ralela a r e s, dividindo o 120° O B em dois (a s ângulo A e b). B Os ângulos a e (3x 2 4°) são colaterais internos, portanto, a 1 3x 2 4° 5 180° V a 5 180° 2 3x 1 4° V a 5 184° 2 3x. Os ângulos b e 120° são colaterais internos, portan B 5 a 1 b to, b 5 60°. Desse modo, tem–se que A O V 2x 1 4° 5 184° 2 3x 1 60° V 2x 1 4° 5 5 244°2 3x V 2x 1 3x 5 244° 2 4° V 5x 5 240° V 240° V x 5 _____ 5 48°. 5 O B, faz2se Assim, para determinar o ângulo A A O B 5 a 1 b V A O B 5 184° 2 3 ? 48° 1 60° V A O B 5 184° 2 144° 1 60° V A O B 5 40° 1 60° V V A O B 5 100° 6 Copie a tabela abaixo em seu caderno e complete–a, efetuando os cálculos mentalmente. x � 2y ___ Se M é o ponto médio de AB , então se tem AM 5 BM. 18 2 x 5 16 ___ 2 y V 2x 5 16 2 y 2 18 V x 5 y 1 2 Como AB mede x 1 2y, tem–se que x 1 2y 5 5 18 2 x 1 16 2 y. Substituindo x por y 1 2 & & y 1 2 1 2y 5 18 2 (y 1 2) 1 16 2 y V 3y 1 2 5 5 18 2 y 2 2 1 16 2 y V 3y 1 2 5 32 2 2y V 30 V 3y 1 2y 5 32 2 2 V 5y 5 30 V y 5 ___ 5 6. 5 Então tem-se x 5 y 1 2 V x 5 6 1 2 5 8. Desse modo, AB 5 x 1 2y V V AB 5 8 1 2 ? 6 5 8 1 12 5 20. Polígono regular Soma dos ângulos internos Ângulo externo Ângulo interno 360° 90° 90° 540° 72° 108° 720° 60° 120° ___ B. Calcule 4 Na figura abaixo, OP é bissetriz de A O B O C. B x � 6° P 4x � 3y y � 1° A C 0 ___ O B. Assim, Se OP é bissetriz de A O B, então A O P 5 P x 1 6° 5 y 1 1° V x 5 y 1 1° 2 6° V V x 5 y 2 5°. O ângulo A O C mede 180°. Assim, 4x 1 3y 1 x 1 6° 1 y 1 1° 5 180° V V 5x 1 4y 1 7° 5 180°. Substituindo x por y 2 5° & & 5 ? (y 2 5°) 1 4y 5 173° V 198° 5 V 5y 2 25° 1 4y 5 173° V 9y 5 198° V y 5 _____ 9 5 22°. x 5 y 2 5° V x 5 22° 2 5° V x 5 17°. Desse modo, tem-se B O C 5 4 ? 17° 1 3 ? 22° V O C 5 68° 1 66° V B O C 5 134°. V B 7 Numa festa havia 18 pessoas, e cada uma cumprimentou as demais uma única vez, com apenas um aperto de mão. Quantos apertos de mão foram dados? Considerando um polígono de 18 lados, em que cada vértice representa uma pessoa da festa, cada aperto de mão corresponde a um lado ou uma diagonal desse polígono. Dessa forma, o número total de apertos de mão corresponde à soma do número de lados com o número de diagonais do polígono de 18 lados. n (n 2 3) ______ 18 ? 15 5 5 135. O número de diagonais é _________ 2 2 Logo o número de apertos de mão é 135 1 18 5 153. 8 Um polígono regular tem soma dos ângulos internos igual a 1 800°. Calcule a medida de um ângulo externo desse polígono. Determina–se o número de lados desse polígono. Si 5 (n 2 2) ? 180° V 1 800° 5 (n 2 2) ? 180° V 1 800° 5 n 2 2 V 10 5 n 2 2 V n 5 12 V ______ 180° Determina–se a medida do ângulo externo. 360° 360° _____ ae 5 _____ 5 5 30°. n 12 65 3P_YY_M8_RA_C02_038a067.indd 65 20.10.08 10:59:40 resolução de atividades Capítulo 2 9 Um programa de computador tem como objetivo fazer um bichinho deslocar–se na tela. A cada 2 cm que se desloca, o bichinho deve girar 15° para a direita (veja figura). Se o bichinho parte do ponto A, quantos centímetros ele percorrerá até retornar ao ponto de partida? 15° C 2 cm 15° B A 2 cm Para retornar ao ponto de partida, o bichinho deve percorrer o perímetro de um polígono cujo ângulo externo mede 15°. Determina–se o número de lados desse polígono. 360° 360° ae 5 _____ V 15° 5 _____ V 15°n 5 360° V n n 360° V n 5 _____ 5 24 lados. 15° Como cada lado do polígono mede 2 cm, o bichinho vai percorrer no total 48 cm. 10 Copie os pontos no caderno, de acordo com a disposição indicada abaixo. Depois indique, para cada item, quantos polígonos de três lados, com vértices nesses pontos, você consegue construir. a) 4 polígonos. b) a) Quantos pentágonos faltam para Joana fechar um colar feito de pentágonos regulares e congruentes, como mostra a figura abaixo? Para fechar o colar, Joana forma um polígono com os lados do pentágono, sendo que o ângulo interno desse polígono é igual a 360° menos o dobro do ângulo interno do pentágono, ou 360° 2 2 ? 108° 5 5 360° 2 216° 5 144°. O ângulo externo desse polígono mede 36°. Assim, 360° seu número de lados será ae 5 _____ 5 10 lados. 36° Como Joana já utilizou 3 pentágonos, faltam, ainda, 7 pentágonos. b) Qual a menor quantidade possível de hexágonos que Joana utilizará para fechar um colar montado com metades de hexágonos regulares divididos como mostra a figura abaixo? Para fechar o colar, Joana forma um polígono com os lados do hexágono, sendo que o ângulo interno desse polígono é igual a 360° menos o dobro do ângulo interno do hexágono, ou 360° 2 2 ? 120° 5 360° 2 240° 5 120°. Assim, como 120° é o ângulo interno de um hexágono regular, o polígono formado por Joana é um novo hexágono, de modo que são necessárias 6 peças para fechá–lo. Como cada peça consiste de um hexágono dividido ao meio, ela precisa de um mínimo de 3 hexágonos, que cortados ao meio produzirão 6 peças. 12 A figura abaixo mostra parte de um polígono regular ABCDE..., onde as ___ retas r e s são perpendi___ culares aos lados AB e CD . Calcule o número de diagonais desse polígono. r s B C A D 60° 0 18 polígonos. Página 73 Questões globais 11 Joana faz bijuterias com peças com formato geométrico. Calcule o material necessário para ela finalizar as peças a seguir. Chamando os ângulos internos do polígono de x, a soma dos ângulos internos do pentágono na figura é x 1 x 1 90° 1 90° 1 60° 5 540° V 2x 1 240° 5 540° V 300° 5 V 2x 5 540° 2 240° V 2x 5 300° V x 5 _____ 2 5 150°. Se o ângulo interno do polígono mede 150°, seu ângulo externo mede 30°. Assim, o número 66 3P_YY_M8_RA_C02_038a067.indd 66 20.10.08 10:59:41 resolução de atividades Capítulo 2 360° de lados desse polígono será: ae 5 _____ V 30° 5 n 360° 360° _____ _____ 5 n V 30n 5 360° V n 5 5 12 30° Determinando o número de diagonais: 12 ? (12 2 3) _____ 12 ? 9 ____ 108 5 54 5 5 D 5 ___________ 2 2 2 13 Um polígono convexo tem a mais que outro 12 lados e 222 diagonais. Quantos lados têm esses polígonos? Se um dos polígonos tem n lados, o outro terá (n 1 12) lados. Assim, o número de diagonais será n ? (n 2 3) _______ n2 2 3n 5 • para n lados & __________ 2 2 • para (n 1 12) lados & (n 1 12) ? (n 1 9) ______________ n2 1 21n 1 108 ________________ 5 2 2 A diferença entre eles será n2 2 3n n2 1 21n 1 108 _______ 2 5 222 V ______________ 2 2 n2 1 21n 1 108 2 (n2 2 3n) ____ 444 5 V V _________________________ 2 2 V n2 1 21n 1 108 2 n2 1 3n 5 444 V V 24n 1 108 5 444 V 24n 5 444 2 108 V 336 V 24n 5 336 V n 5 ____ 5 14 24 Logo, um polígono tem 14 lados, e o outro, 26 lados. 14 Juliana decora camisetas. Ela gosta de utilizar polígonos regulares em seus trabalhos. Em algumas camisetas, ela desenha as figuras e nas diagonais cola fitas de tecido decoradas. Por causa disso, o preço da decoração dessas camisetas varia de acordo com o polígono regular desenhado. a)Sabendo que cada diagonal decorada com fita || 0,35, copie a tabela no caderno e comcusta RS plete-a, indicando o custo da decoração das camisetas de acordo com o polígono desenhado. Calcula–se primeiramente o número de diagonais. || 0,35 Em seguida multiplica-se esse número por RS para obter o custo. n (n 2 3) ____ 4?1 Quadrado & D 5 _________ 5 5 2 2 2 Custo 5 2 ? RS|| 0,35 5 RS|| 0,70 n (n 2 3) _____ 5?2 Pentágono regular & D 5 _________ 5 5 5 2 2 Custo 5 5 ? RS|| 0,35 5 RS|| 1,75 n (n 2 3) _____ 6?3 5 Hexágono regular & D 5 _________ 5 9 2 2 Custo 5 9 ? RS|| 0,35 5 RS|| 3,15 n (n 2 3) _____ 7?4 5 14 Heptágono regular & D 5 _________ 5 2 2 Custo 5 14 ? RS|| 0,35 5 RS|| 4,90 n (n 2 3) _____ 8?5 5 20 Octógono regular & D 5 _________ 5 2 2 Custo 5 20 ? RS|| 0,35 5 RS|| 7,00 n (n 2 3) _____ 9?6 5 27 Eneágono regular & D 5 _________ 5 2 2 Custo 5 27 ? RS|| 0,35 5 RS|| 9,45 n (n 2 3) _____ 10 ? 7 5 35 5 Decágono regular & D 5 _________ 2 2 Custo 5 35 ? RS|| 0,35 5 RS|| 12,25 n (n 2 3) _____ 11 ? 8 5 44 Undecágono regular & D 5 _________ 5 2 2 Custo 5 44 ? RS|| 0,35 5 RS|| 15,40 n (n 2 3) 12 ? 9 5 54 5 _____ Dodecágono regular & D 5 _________ 2 2 Custo 5 54 ? RS|| 0,35 5 RS|| 18,90 Custo da decoração Nome do polígono || 0,70 RS quadrado || 1,75 RS pentágono regular || 3,15 RS hexágono regular || 4,90 RS heptágono regular || 7,00 RS octógono regular || 9,45 RS eneágono regular || 12,25 RS decágono regular || 15,40 RS undecágono regular || 18,90 RS dodecágono regular b) Juliana compra uma cami|| 15,00 e deseja seta por RS revendê-la, após fazer a decoração, de modo que o valor ob|| 5,00 tido com a venda seja RS maior que o valor do custo total da camiseta. Qual deve ser o preço de venda da camiseta ilustrada? Como a camiseta contém um pentágono regular, o custo da decoração é RS|| 1,75. Portanto, o custo total da camiseta decorada é RS|| 15,00 1 RS|| 1,75 5 RS|| 16,75. Se ela quer revender a camiseta por um preço que é RS|| 5,00 maior do que o custo, esse preço de venda é RS|| 16,75 1 RS|| 5,00 5 RS|| 21,75. 67 3P_YY_M8_RA_C02_038a067.indd 67 20.10.08 10:59:41
Download