R. de Econometria
Rio de Janeiro
v. VI
n9 2
p.
47
-
68
nov
1986
ESTIMAÇÃO DO HIATO DO PRODUTO VIA COMPONENTES NÃO OBSERVADOS
Pedro
Luiz
Valls
pereira*
RESUMO
o Hiato do Produto é usualmente definido pela diferença entre
o logaritmo do produto potencial e o logaritmo do produto efetivo,
onde o produto potencial é definido pela estimativa do nível que o
produto real atingiria se houvesse pleno emprego.
Está implicito na definição de produto potencial um crescimen
to continuado. Alguns autores criticam esta formulação (veja por �
xemplo Moreira (1985)) e supõem que, considerando-se o produto in­
dustrial, empresários prevêem o crescimento do ano
I
como a
média
das taxas verificadas nos dois últimos anos. E investimentos
são
realizados de forma a manter o grau de utilização do parque indus­
trial constante.
Apresenta-se neste artigo uma forma alternativa de definir
o
produto potencial que está associada à formulação tradicional. Ne�
ta formulação o produto potencial é definido pela componente de�
dência da série do produto efetivo, podendo estar presente
outros
componentes tais como as de ciclo e sazonalidade.
Portanto o produto efetivo pode ser interpretado como uma sé­
rie temporal que pode ser decomposta em componentes não observados,
i.e., um modelo estrutural na terminologia de Harvey (1985 ) .
*
INSTITUTO DE PESQUISAS DO IPEA
48
REVISTA DE ECONOMETRIA
A estimativa dos componentes não observados é feita pelo Fil­
tro de Kalman e como subproduto tem- se a estimativa do hiato
do
produto como a diferença entre o produto efetivo e a componente de
tendência. Também como subproduto é possível obter uma série
do
produto efetivo e do potencial num nivel diferente do o�acional.
A BSTRACT
The Product Gap 1s usually defined by the difference
between
the logarithm of potential product and that of effective
product,
the former being defined by the estimate of the level that the real
product would reach if there were full employment.
Sustained growth 1s implicit in the definition of
product. Some authors (5uch as Moreira (1985»
have
potential
criticized
consider
this forrnu!ation, and suppose that when entrepreneurs
the industrial product, they make a provision for the year' s �
using the average rate of the two previous years. AIso,
are realized so as to maintain the utilization of the
invesbrents
industrial
complex at a constant leveI.
This article presents an alternatlve way of defining
poten­
tial product, one associated with the traditional formula.
This
new formulation defines potential product by the trend componentof
the effective product series, with the possible presence of
other
components such as cyclical and seasonal.
Effective product may therefore be interpreted as a
temporal
series that can be broken up into non-observed components, i.e., a
structural model in the terminology of Harvey (198S}.
The estimate of the non- observed components is made by Ka�'s
Filter; as a by-product we have the estimate of the product gap as
the difference between effective product and the trend
Another by-product that may be obtained is a series
of
component.
effective
and potential product on a different leveI from the observational.
NOVEMBRO DE 1986
I.
49
INTRODUÇM
o Produto Potencial é usualmente definido pela estimativa
nível que
o
do
produto real atingiria se houvesse pleno emprego.
malmente, denotando- se o produto por Y e assumindo-se um
t
mento exponencial , estima-se a regressão:
For
cresci­
a + bt + u
t
(1 • 1 )
e o produto potencial (denotado por P ) é definido por:
t
â + :6t
(1 .2)
Está implícito nesta formulação um crescimento continuado/que
é pouco razoável para uma economia como a brasileira. Além disto a
suposição de uma tendência global é pouco satisfatória do ponto de
vista estatístico e econômico, pois há várias mudanças que
tornam
esta hipótese improvável.
Urna formulação alternativa proposta por Moreira
definir o Produto Potencial Industrial , supõe que os
(1985)
para
industriais
sejam conservadores tanto quanto às expectativas de crescimento
e
ao nível de investimento.
Moreira (1985) assume que este conservadorismo pode ser
ex­
presso, pelo lado das expectativas de crescimento, pela hipótese de
50
REVISTA DE ECONOMETRIA
que a taxa de crescimento do setor industrial num ano é uma
das taxas verificadas nos dois últimos anos. E pelo lado
média
do nível
de investimento , os empresários investiriam de acordo com as expeE
tativas de crescimento de forma a manter constante o grau de uti!i
zação do parque industrial. Formalmente, e utilizando-se a notação
é a taxa de crescimento do setor
indus­
t
trial e u o grau de utilização, �stas duas hipóteses podem
ser
t
expressas por:
de Moreira (1985 ) , se g
g
*
t
*
u
t
g
t-l
+
g
2
t-2
(1. 3)
u
t_1
onde por definição g
t
�
=
y t-l
-
1 e u
t
=
Utilizando-se a hipótese de que o esperado é igual ao realiza
do, por (1.4) obtém-se que:
(1 . 5)
1
+
que:
a
Mas pela definição de 9 tem-se que (1.5) é equivalente
t
g " Novamente utilizando- se a hipótese de que gt
g '
tem-se
t
t
=
(1.6)
2
observe que (1.6) pode ser reescrito da seguinte forma:
(1. 7)
onde , por definição, A
t
da variável A .
t
- 1, i.e. , a taxa de
crescimento
51
NOVEMBRO DE 1986
Como P
6P tem-se que enquanto em ( 1.2) a taxa de cresci­
t
t
mento do Produto Potencial é constante e igual a b, nesta outra for
=
mulação ela é uma média móvel, de segunda ordem, da taxa de cresci
menta do Produto Efetivo defasada num período.
Embora a formulação de Moreira
(1985)
seja menos
problemáti­
ca do que a usual, ambas não utilizam informações importantes
série de produto, já que é difícil acreditar que não exista,
da
pelo
menos, urna componente cíclica associada à série de Produto Efetiv�
Nestas duas formulações esta possível componente é ignorada.
Propõem-se que a série de Produto Efetivo possa ser
escrita
como um modelo estrutural de série temporal, i.e.:
(1.8)
onde � é a componente de tendência, Y a de sazonalidade, � a de
t
t
t
ciclo e E o componente irregular. O Produto Potencial será então
t
definido pela componente � em (1. 8) e o hiato do Produto por:
t
Este artigo está organizado da seguinte maneira: na Seção
apresenta- se a formulação de modelos estruturais de séries
2
tempo­
rais. Na Seção 3 é apresentada a estimação destes modelos por Máx!
ma Verossimilhança através do Filtro de Kalman. Também se
aprese�
ta um método para estimar as componentes não observadas de (1.8) .
Na Seção 4 aplica-se esta técnica nas estimativas do
Potencial da Economia e do Potencial para a Indústria.
Produto
52
REVISTA DE ECDNDMETRIA
2.
MDDELDS ESTRUTURAIS DE SeRIES TEMPDRAIS
2.1
Introdução
Historicamente Séries Temporais eram decompostas em componen­
tes de tendênci a , ciclo , sazonal idade e irregular, i.e.:
(2.1)
Este procedimento foi relegado a segundo plano com a introdu­
ção dos modelos ARIMA, que está intimamente ligada ao aparecimento
do livro de Box & Jenkins (1976) cuja primeira edição foi publica­
da em 1970.
A metodologia de Box & Jenkins pode ser interpretada como
a
forma reduzida de um modelo da forma (2.1) , como veremos a seguir.
Por outro lado, devido à facilidade de utilização desta
metodolo­
gia , os modelos da forma (2.1) foram considerados "ad- hoc" e
com
pouco embasamento teórico.
Nesta mesma década Harrison & Stevens (1976) apresentaram
o
Procedimento Bayesiano de Previsão que está relacionado à especif!
cação de uma série de tempo em componentes como a descrita
(2.1)
por
•
Este procedimento permitiu dar uma " teoria" para a
modelagem
de uma série por componentes não observados, como (2.1) . Mas
al-
guns pontos fundamentais desta modelagem ainda permaneceram basta�
te " ad-hoc", Somente na década dos 80 com os trabalhos de Harrison
e seus associados , foi possível justificar a "estimativa"
seqüên­
cial das variâncias dos componentes [veja por exemplo West et ali i
(1985) 1
•
Com a introdução do Filtro de Kalman para a estimação de
ries temporais [Akaike (1974) ou Harvey (1981)
sé­
para uma sistemati-
53
NOVEMBRO DE 1986
zação deste procedimento)
I
foi possível dar uma interpretação clá�
sica ao Procedimento Bayesiano de previsão, pois este procedimento
de "estimacão", está relacionado com o Filtro de Kalman que é
um
método para se obter a verossimilhança de modelos.
A principal vantagem do Procedimento Bayesiano de Previsão
é
o custo computacional, já que a estimação por Máxima Verossirnilha�
ça de modelos da forma (2.1) consome bastante tempo de máquina.
Engle (1978) introduziu o conceito de modelo estrutural em sé
ries Temporais que é uma volta à formulação de uma série via comp�
nentes não observados do tipo (2.1).
Posteriormente Harvey & Todd (1983) especificam cada um
componentes de (2.1) de uma forma bastante semelhante à de
dos
Harri­
son & Stevens (1976) .
2.2 Componente de Tendência
Para a componente de tendência, em vez de assumirmos uma ten­
dência global, adotaremos a formulação que aproxima localmente es­
ta tendência.
Por exemplo, se a tendência puder ser representada por
função linear no tempo, em vez de assumirmos a
tendência
uma
global,
Le.:
(2 2)
.•
assumiremos que esta formulação é válida localmente, isto é,
tanto o nível desta tendência
[i.e., a em (2.2)] quanto a taxa
crescimento [i.e., b em (2.2)], evoluem suavemente ao longo
tempo.
Denotando o nivel por �
t
e a tendência por 6 , tem-se que:
t
que
de
do
54
REVISTA DE
ECONOMETRIA
(2.3)
(2.4)
onde n
e � são ruídos brancos não correlacionados com médias ze­
t
t
ro e variâncias o e o respectivamente.
�
�
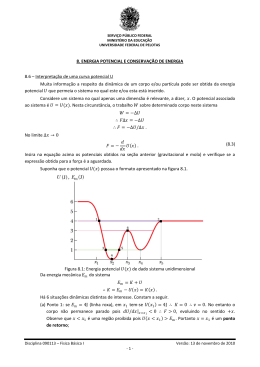
Se o processo de geração dos dados for uma tendência mais er­
ro, i. e.:
(2.5)
\lt + E:t
onde E: é ruído branco independente de n e S ' com média zero
e
t
t
t
variância de o�, tem-se que o modelo é dado pelas equações (2.5),
(2.4) e (2.3), que representa a forma estrutural de um modelo ARI­
MA.
A forma reduzida para as observações é obtida observando-se
que a equação (2.3) pode ser escrita da seguinte forma:
(2.6)
(1 - L)
substituindo- se (2.6) em 2.4), obtém- se:
+
(1 - L)
(1 - L) �
(1
-
L)
(2.7)
e substituindo-se (2.7) em (2.5), obtém-se:
(1
-
L) 'Y
t
(2.8)
55
NOVEMBRO OE 19B6
que corresponde a um ARlMA (0,2,2) com restrições nos
parâmetros
do MA.
2.3 Componente de Ciclo
A segunda componente que pode estar presente em séries econô­
micas é a do ciclo. POderíamos modelar a componente de ciclo
por
um ARMA (p,q). Na literatura [veja por exemplo 'Priestey (1981)]
o
modelo mais usado é o AR(2), já que este modelo pode gerar movime�
tos senoidais amortecidos.
Na formulação alternativa, proposta por Harvey (1985), denot�
-se a componente cíclica por �t' e assume-se um modelo estacioná­
rio centrado na freqüência À que pertence ao intervalo [O, TI].
A
c
formulação estatística é dada por:
p
(
C OSÀ
C
(2.9)
-sinÀc
Kt e Kt são ruídos brancos não correlacionados com média ze­
ro, variância comum a� e O, que pertence ao intervalo [0,1), é o
onde
coeficiente de amortecimento.
t fácil mostrar que a forma reduzida de (2.9) é dada por:
K**
t
onde
Kf*
pode ser escrito como um MA(1) com parâmetros e e
estes parâmetros são as soluções das equações:
(2.10)
cr�**
e
(2.11)
(2.12 )
56
REVISTA DE ECONOMETRIA
g também fácil mostrar que a é a solução real, que satisfaz a
condição de invertibilidade, de uma equação de 29 grau.
Observe que (2.10) implica num modelo ARMA (2,1l onde as
raí­
zes do polinômio da componente autoregressiva são os complexos eon
jugados p (cosÀ ± i sinÀ )' cujo módulo é menor do que um, já
c
c
p E [0, 1).
que
Observe também que existe uma relação não linear entre os pa­
râmetros do componente autoregressivo e os do componente média -mó­
vel de (2.10). Defina � e � como os coeficientes de L e L2 no p�
2
1
linômio do lado esquerdo de (2.10). Tem-se que o lado direito
de
(2.11) é dado por (1 - q, )a � e o de (2.12) por
2
(- .Pi )o�.
..
2.4 Componente de Sazonal idade
A componente sazonal, denotada por Y
é definida corno a soma
t
cada um deles tendo uma especificaçãodo
de s fatores sazonais Y
j,t
tipo (2.9) com p igual a um e a freqüência À igual a uma dada fre
c
i.e.,
qüência sazonal, denotada por À
j
�,
=
s/2
E
(2.13)
j 1
=
onde
se j=l, ...
)( ) ( )
,(�)-l
SinÀ
j
y
cosÀ.
J
Y�
J, t- 1
j,t-1
+
Wj't
(2.14 )
w J,
. t
e
(coSÀ.)y.
J J, t-1
+
w .
J, t
(2.15 )
NOVEMBRO DE 1986
57
5
2 e var(w
se j
j,t
) = var(w
j, t)
cr�
=
para todo j.
t fácil mostrar que a forma reduzida de (2.14) é dada por:
(1 - 2cosÀ.L + L2)y.
J
J ,t
para j=l,
.
. •
,
�
{ )
-
l com 9
j
(2.16)
j�t
= -secÀ T tanÀ e w
j
j
'
cr
cos independentes com var(w�* ) =
J ,t
_
são ruídos bran-
w
�
(l±SinÀ )
j
______
__
E a forma reduzida de (2.15) é dada por:
(2.17)
Portanto (2.13) é equivalente a:
�
( -1)
Y
t
r
j=1
+
(1
e .L) w1:'*.
]
J ,t
1 - 2cOSÀ L + L'
j
+
Ws
2 ,t
1+L
(2.18)
� fácil mostrar que
(2.19)
e que
(l+L)w1:* :: w-,;** = MA{S - 2)
)rt
],t
para J=
. 1"
"
s
.
'2 - I
e
que
(2.20)
58
w***
s
2 ,t
e o numerador de (2.18) sendo a soma de
�
REVISTA DE
E CONOMETRIA
MA(s - 2)
(2.21)
MA(s-2) independentes
também um MA(s-2). Portanto tem-se que S(L) Y
t
�
é
MA(s-2).
2.5 Componente Irregular
o componente irregul�r, denotado por � ' é geralmente assumi­
do ser um ruído branco com variância
o�,
t
exceto quando tem-se algE
ma informação lia priori" sobre este componente para se modelar por
um processo estacionário do tipo ARMA(p , q).
Se o processo de geração dos dados puder ser representado por
urna série temporal que possa ser decomposta em componentes dos ti­
pos descritos acimar e estes componentes entram de forma
aditiva ,
tem- se que este processo pode ser caracterizado por:
(2.22)
� fácil ver que a forma reduzida do modelo estrutural
geral
é dada por:
ââ <1 - 2pcoSÀ L + P2L2)Yt=âs<1-2pcoSÀcL+p2L2)nt
c
S
+S(L)(1 -2pcoSÀ L+p2L2)
l;:t_1
c
+ (1 - eL)t:.t:. K�*
s J,t
+MA(s"- 2)t:.2W�**
] ,t
+l::.l::. {1 - 2pcoSÀ L+p2L2)E
t
s
c
(2.23)
59
NOVEMBRO OE 1986
3.
FORMULAÇ�O DE MODELOS E M ESPAÇO DE ESTADO
Dada uma série temporal Y a representação desta série em es­
t
paço de estado é dada pelas equações de medida , i.e.:
(3.1>
com var(� )
t
do a , i.e.:
t
=
a�
e de transição, que dá a evolução do vetor de est�
(3.2)
com Var(S )
t
=
Q.
� fácil ver que a representação dos modelos estruturais em e�
paço de estado é dada pelas equações
(3.1-2) onde o vetor de esta­
do é dado por:
(3.3)
e o vetor z na equação de medida é dado por:
z
=
[1,0;
l,Oi 1,0, •
• •
,1,0]
(3.4)
A matriz de transição T é facilmente obtida pelas equações que
definem cada um dos componentes.
o erro da equação de transição é definido por:
(3.5)
REVISTA D E ECONOMETRIA
60
e a matriz R é definida por:
1
O
O
R
O
O
O
O
O
O
O
O
O
O
O
O
O
O
O
O
1
O
O
O
O
O
O
1
O
O
O
O
O
0
O
O
0
O
0
0
O
O
1
O
0
e a matriz de variância e covariância de S é definida por:
t
Q
3.1
Estimação dos Parâmetros no Dominio do Tempo
Se os erros em (3.1) e (3.2) têm distribuições normais, a fun
cão de verossimilhança para o processo de geração dos
dados
ser obtida pelo Filtro de Kalman utilizando-se a decomposição
pode
do
erro de predição {veja Harvey (1981)]. A estimativa dos parâmetros
pode ser obtida por urna rotina numérica que maximizará a verossim�
lhança, i.e. :
10g L
T
1
- (2 )109 (2"1 - 2
T
E 109f
t 1
t
(3.6)
=
onde v é o erro de predição um passo à frente e 02 f é a variância
t
t
'
do e rro de predição, e estas quantidades são obtidas pelo Filtro de
Kalman.
Para se iniciar as recursões do Filtro de Kalman,
necessita­
- se de valores iniciais para a média e variância do vetor de esta­
do, denotados por a
O
e
a2Po'
NOVEMBRO DE 1986
61
No caso d e modelos estruturais existem várias formas d e
ini­
ciar estes dois valores , mas adotaremos a forma mais simples que é
assumir a
O
= O e
P'o
=
K 1,
onde
K
é um número grande.
Este procedimento corresponde a assumirmos que o vetor de esdifusa
tado no instante inicial tem uma distribuição "a priori"
[para maiores detalhes veja Harvey & Peters
(1984)].
3.2 Estimação de Modelos Estr uturais com Falta de Observação
Suponha que as observações são feitas a cada ô período de te�
pc, onde ó é um inteiro positivo. Para variáveis de estoque
isto
quer dizer que:
1, •
T
e para t � 0"
• •
(3.7)
,T
Yt é não observado. Para variáveis de fluxo tem-se:
6-1
í:
r=O
YÓ,_r para T
1,•
• •
,T
(3.8)
Algumas vezes as variáveis de estoque são medidas pela
no período de observação. Neste caso deve-se tratar esta
média
variável
como do tipo fluxo já que as observações são dadas por:
6-1
1
"6
E
r=O
yó
T-r
para T
1,... ,T
(3.9)
A estimação dos parâmetros é feita utilizando-se o Filtro
Kalman. A representação em Espaço de Estado , dada pelas
(3.1-2),
t = 1,
• • .
é válida para o intervalo de tempo unitário, i.e. ,
,õT.
de
equações
para
62
REVISTA DE ECONOMETRIA
Para o caso de variável de estoque não é necessário fazer ne­
nhuma modificação nas equações (3.1-2). Mas como o período de
servação é dado por t
o,2ô, ... ,6T, as equações de
são puladas para todo t
� 6,26,...,OT.
ob -
atualização
Para o caso de variáveis de fluxo, é necessário aumentar o ve
tor de estado. Neste caso o novo vetor de estado é definido por:
(3.10)
f
on de Y e"
t
efinido por:
(3.11)
onde � é definido por:
t
�
o
t
para t
=
+
6(1:-1)
1 , 1"
1,
• • •
,T
(3.12 )
caso contrário
� fácil ver que a nova equação de transição para o vetor
de
estado é dada por:
( ) ( I{I�\( \) (R ) ( \)
T
at
Y
�
=
O
z' T
at _ 1
:�-1
+
z' R
O
St
1
E: t
(3.13)
e a nova equação de medida é dada por:
Y,
(O'
l)C;}
t
ô, ,
O filtro é iniciado como a
f
O
,
1, ... ,T
(Õ,O)
f
e p
O
(3.14 )
d.
NOVEMBRO OE
63
1986
3.3 Interpolação e Distribuição das Observações Intermediárias
Interpolação de observações faltando é facilmente obtida usan
do- se um algoritmo de suavizamento de ponto fixo [veja Anderson
Moore (1979), Capítulo 7]. O estimador das observações
&
intermediá
rias é dado por:
1,
• • .
(3.15 )
,T
denota o estimador de suavizamento do vetor de estado �
onde a
t/ÔT
sando a informação até o tempo t
óT.
=
Distribuição de variáveis agregadas temporalmente também
po­
dem ser obtidas através de um algoritmo de suavizamento. Neste ca­
so deve-se adicionar mais um componente ao vetor de estado de for�
ma a obter as observações intermediárias.
Neste caso o novo vetor de estado é definido por:
(3.16)
e adiciona-se uma linha na matriz de transição que cor responde
decomposição da série nos componentes não observados , i.e.,
à
equa­
cão (3.1).
4.
APLl CACOES
Esta seção apresenta os resultados obtidos
com
TEMPAGG.SMS que estima modelos estruturais de séries
o
programa
temporais
com falta de observação ou agregação temporal.
Este programa obtém os estimadores de máxima
verossimilhança
para as variâncias dos diversos componentes, maximizando a
função
de verossimilhança no domínio do tempo, utilizando a rotina E04JBF
da biblioteca de programas da NAG. Esta rotina é da classe
Newton e permite a maximização com restrições.
Quasi­
REVISTA DE ECONOMETRIA
64
Este programa também permite obter as estimativas das observa
côes entre pontos intermediários, i.e., as interpolações se a
sé­
rie sob consideração é do tipo estoque e as distribuições das
ob-
veja
servações se do tipo fluxo. Para alguns exemplos
Pereira
(1986).
Utilizou-se o Produto Industrial e uma série do PIB real
cruzeiros de 1970) construída a partir do índice do Produto
(em
Real
Total. As fontes para os indices de Produto são Zerkowiski & Velo50
(1982) para os anos de 1920 a 1980 e Contas Nacionais / Conjun­
tura Econômica para os anos de 1981 a 1984.
o modelo especificado foi do tipo Tendência
+
Ciclo
+
Irreg�
lar. Devido à definição de hiato foi necessário utilizar a transfor
mação logarítmica nos dados. Desta forma a componente de tendênci�
que representará o produto potencial, é dada pelas equações (2.3-4l
Para a série do PIB Real as estimativas dos parâmetros
obti­
das pelo programa TEMPAGG.SMS foram:
o'E
0.0000
o'n
0.0000
a'
<
'
a
K
À
c
p
.1212*10
.1103*10
-4
-4
(.1010*10 )
-2
-3
(.2217*10 )
1
.3826(.6180*10 - )
-1
.9012(.4186*10 )
onde os valores entre os parênteses são os desvios das estimativas.
Pelas estimativas dos parâmetros observa-se que:
i) a forma reduzida correspondente a um modelo ARlMA(2,2,3)
com restrições não lineares entre os coeficientes do componente AR
e do MA;
ii) embora a variância do nível da tendência seja não
nula,
a um nível de significância de cinco por cento, não se pode
reje!
tar a hipótese de que esta variância não é significantemente dife­
rente de zero. Tem-se, portanto , que as variâncias da taxa de cres
cimento e do nível da tendência são nulas implicando numa
cia determinística;
tendên­
NOVEflBRO DE 1986
65
iii) tem-se , portanto, que o modelo que descreve a série
PIB Real
do
é do tipo tendência determinística mais ciclo;
iv) pela estimativa da amplitude, tem-se que o período do ci
cIo, definido por
�-±,
é de 16 anos e 5 meses.
c
A estimativa do hiato do PIB Real é apresentada no Gráfico 1.
GRÁ1'l(:O 1
0,12
o. ,
HIATO DO PRODUTO REM. TOTAl.
-r------------------------------------------------------..------
o,os
t\. ."
O,Oh
I
,
0,04
-0,02
-o,
\\
O�
t
',I t':{ \
\
i
f
�
�----_+------�
"
I ��
o ++, �
, H__t_,��+_
0,02
\
.�
"
\
.;
I
I
I
i
-0,06
-0,08
\1
-O. 1
-o,
I
+.
12
- O. lf.
-O·'"
,
f,TTrrnn<nnnnnTTnrnnTrnnTTrnornrrrl
1920
1930
1940
H IATO
19S0
DO
19bO
1970
1')80
PRODUTO R E A L
1920
1930
1940
1950
1960
1970
\980
-0.0113
-0.0195
0.0356
-0.0008
0.0766
-0.0596
0.1049
-0.0388
-0.0951
-0.0714
0.0035
0.0705
-0.0162
0.0181
0.0229
-0.1179
-0.0448
-0.0035
0.0097
0.0196
-0.0208
-0.0069
-0.0345
0.0814
-0.1255
0.0235
-0.0834
0.1036
-0.1416
0.0746
-·).0429
-0.0534
0.0314
-0.0025
-0.082
0.0011
0.0683
-0.0266
-0.0217
-0.1017
0.0917
-0.0295
0.0564
-0.041
-0.0107
-0.1279
0.1182
0.0232
0.0573
-0,0125
0.0207
-0.0955
0.1062
0.1084
0.0486
0.0128
0.0441
-0.0687
0.0891
0.0649
0.0115
O. 0195
0.073
-0.0687
0.0907
66
REVISTA DE ECONOMETRIA
Para a série do índice do Produto Industrial as estimativas
dos parâmetros obtidas pelo programa TEMPAGG.SMS foram:
-3(.4158*10 -3
)
o'
E
.1374*10
a'
2
7
.3853*10- (.2443*10- )
a'
4
4
.2018*10 - (.2371*10 - )
'
a
K
.1826*10
À
c
.3737(.6153*10
n
;;
P
-2
-2
(.1661*10 )
-1 )
1
.9191 (.5486 *10 - )
Pelas estimativas dos parâmetros observa-se que:
i) embora as variâncias do nivel e da taxa de crescimento da
tendência sejam não nulas, a um nivel de significância de cincopor
cento, não se pode rejeitar a hipótese de que estas variâncias não
são significativamente diferentes de zero.
Tem-se, portanto,
as variâncias da taxa de crescimento e do nível da tendência
que
são
nulas implicando numa tendência determinística;
ii) embora não se possa rejeitar a hipótese de que a variân­
eia do ciclo seja nula, optou-se por manter este componente já que
ao se comparar o modelo estimado com um somente componente de ten­
dência, o modelo menos parcimonioso foi aquele que apresentou
me­
nor A.I.C.;
iii) tem-se, portanto, que o modelo que descreve a série
do
Pr9duto Industrial é do tipo tendência determinística mais ciclo;
iv) pela estimativa da amplitude tem-se que o período do ci­
clo, definido por
i$,
c
é de 16 anos e 10 meses.
A estimativa do hiato do Produto Industrial é apresentada
Gráfico 2 a seguir.
no
67
NOVE MBRO DE 1986
0,25
GRÁFICO
,___________________________-----,
0,2
,�
;
0,15·
I I,
-0,05
I
,
:
0,05
o
I
T,
.
O,,
"\'-
H
•
;li
\1\
"
-0,15
-0,2
\t.!
i\i
r
/
II
I
\1
')
-0,1
-O.25
2
HIATO DO PRODUTO INDUSTRIAL
;.
..
,\
I
l
'li
\
;
\
\1
i
:t
�'\
T/
,
,
,
,
I
,
r
\, l
'"
'l. r
'J
,
..
�rnrrrrrnrn"""TTTTrrnnrnrn""<TTTrrnrrnrnnn_n4
1920
1930
1940
1950
1960
1970
1980
H I A T O DO PRODUTO INDUSTRIAL
1920
1930
1940
1950
1960
1970
0.02019 -0.13041
0.0702
0.0281
0.0759
-0.0537
0.1286
-0.03315 -0.18839
0.0822
0.0184
0.0886
-0.0168
0.0075
1980
0.15369 -0.2251
-0.0198
-0.0005
0.0836
0.0294
-0.0509
0.20553 -0.159
-0.041
0.0221
0.0104
0.1052
-0.1843
0.07664 -0.074
-0.0581
0.0034
-0.0166
0.1208
-0.1905
0.1067
-0.0797
0.0161
-0.1237
-0.00468
Q.0519
-0.0198
0.0001
-0.1096
0.1531
0.03787
0.0735
-0.0597
-0.0313
-0.158
0.1224
0.07106
0.0636
-0.1071
0.0311
-0.1133
0.1241
0.01504
0.1018
0.0111
0.0492
-0.076
0.1188
0.04931 -0.0097
68
REVISTA DE ECONOMETRIA
REFE RtNCIA S BIBLIOGRAFICA S
AKAlKE, H. MaJLkoVMm RepJte.óenta..ti.on. 06 Stocha.ó:tJ..c '0loc.e.Q·M6 and U6 appUca.:t..i.ol1.6
to the Ana11j-64 06 Autolleglluó,[ve.-Mov.tl1g
Institue Df Statistical Mathematics, 26, 363-387,1974.
ANDERSON, B. D. O. & MOORE, J.B.
Hall.. 1979.
nox, G.E.P. & JENKINS, G.M.
Dpcimal Filtering, Englewood Cliffs: Prentice
Time Series Analysis, Forecasting and Control, são
Francisco: Holdeu-Day. 1976.
Conjuntura Econômica, 1985.
(ed.)
ENGLE, R.F. E6UnJa-ti119 StJLue:t1lhAl. Modw 06 SeMona1J..ty. em A. Zellner
Seasonal Analysis of Economic Time Series, Bureau of Census, Washington, 281
-308, 1978.
&tye.6.ta.n
HARRISON. P.J. & STEVENS. C.F •
Royal Statistical Society, B, 38,205,247.,1976.
HARVEY, A.C.
ur
J"
o"
.
=n ,--,o"
"
,
Time Series Models, Deddington: Philip Allan, 1981.
HARVEY, A.C. TlLenCÍ6 a.t1d Cycieó -i.J1 MacJt.oec.oJ1omic.
ness and Economic Statistics, 3,216-227, 1985.
HARVEY, A.C. & PETERS, S.
E6
. ru
ModelA, LSE Econometrics programme Discussion Paper, A.44,1984.
MORElRA, A.R.
SvUeó
Baianco de Pa.gamento.6
1985.
PEREIRA, P.L. V.
E6rula.ç.ã.o de Mode1.o.ó E.ó;tlw;twl.ilÁ.h de Svu.eó TempoJtai...6 c.om FaLta.
de. Ob.óVLvacão, artigo apresentado no V Encontro Regional da Região
Sudeste
da S.B.E., Piracicaba, São Paulo, 1986.
PRIESTLEY, M.
Spectral Analysis and Time Series, New York: Academic
Press,
1981.
WEST, N.; HARRISON, P.J. & MIGON, H.S.
Vyna.nú.c. Genvta..ttzed U.neM Modeló
Ba.yeó.w.n FOILe.c.a6üng, Journal of the American Statistical Association,
73-97,1985.
ZERKOWSKI, R.M. & VELOSO, M.A.G. Slli dec.adM de Ec.onomi.a. BJtMileiJta.
do PIB, Revista Brasileira de Economia, 36,331-338,1982.
and
80,