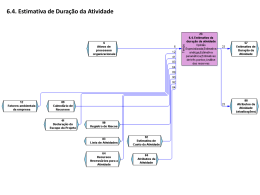
MODELAGEM E SIMULAÇÃO COMPUTACIONAL DA NÃO LINEARIEDADE DE FOLGA
EM UM ROBÔ GANTRY
Odair Menuzzi1, Eduardo Padoin 2, Antonio Carlos Valdiero 3, Antonio Luis Rasia4
1
UNIJUÍ, Caixa Postal 121, Av. Rudi Franke, 540, CEP 98280-000, Panambi - RS, Brasil, [email protected].
UNIJUÍ, Caixa Postal 121, Av. Rudi Franke, 540, CEP 98280-000, Panambi - RS, Brasil, [email protected].
3
UNIJUÍ, Caixa Postal 121, Av. Rudi Franke, 540, CEP 98280-000, Panambi - RS, Brasil, [email protected].
4
UNIJUÍ, Caixa Postal 121, Av. Rudi Franke, 540, CEP 98280-000, Panambi - RS, Brasil, [email protected].
2
Resumo: Trata-se da modelagem matemática e da
simulação computacional dos efeitos da não linearidade de
folga no acionamento de uma transmissão tipo fuso de um
robô Gantry. A modelagem matemática da folga pode
contribuir para estratégias de controle preciso e para
melhoria do desempenho de robôs de baixo custo.
Palavras-chave: modelagem matemática, não-linearidade
de folga, manipulador robótico Gantry.
1. INTRODUÇÃO
Este trabalho trata do problema de modelagem
matemática e simulaçao computacional da não linearidade
de folga (backlash) em transmissões mecânicas do tipo fuso
(parafuso de potência), comuns no acionamento das juntas
prismáticas de robôs Gantry [1, 2, 3, 4]. Tais robôs têm
grande potencial de aplicação nas indústrias do setor metal
mecânico, principalmente devido à sua estrutura rígida, seu
amplo espaço de trabalho em mesas e a facilidade de
programação proveniente do desacoplamento dinâmico entre
o movimento de seus elos. Um dos problemas que
dificultam o controle preciso dos movimentos de um robô
Gantry é a não linearidade de folga no acionamento,
principalmente nas transmissões mais simples e baratas do
tipo fuso roscado.
Atualmente há duas formas de acionamento das juntas
de robôs industriais. Uma é o acionamento direto (directdrive), onde o motor é montado diretamente no eixo da junta
e que de acordo com Turner et al. [5] não é o ideal para
motores elétricos, pois a ausência de uma relação de redução
do movimento leva à necessidade de motores elétricos
especiais com menor rotação e maior torque, além de
sujeitá-lo aos efeitos dinâmicos do acoplamento. A outra
forma de acionamento, que é a mais tradicional e simples, é
a utilização de transmissões por engrenagens entre os
motores e as juntas, as quais possuem como vantagens a
menor carga no motor, maiores rotações no motor e a
facilidade de posicionamento deste no braço do robô. A
desvantagem deste tipo de acionamento é a presença de
atrito e a folga nas transmissões de engrenagem.
De acordo com Ross et al. [6], na seleção ótima de uma
transmissão por engrenagens para aplicações em
mecatrônica, a escolha do tipo depende de muitos fatores,
onde os mais importantes são velocidade de entrada, folga,
eficiência e custo. Em geral a transmissão de custo menor
tem a maior folga, então ou se aumenta o custo ou se
compensa a não linearidade de folga no esquema de
controle. O importante é se chegar a uma solução de
compromisso (trade-off), equilibrando os custos de
fabricação e os custos de implementação de controle com
compensação das não linearidades.
Valdiero [7] aponta a importância do estudo das não
linearidades dos sistemas mecânicos, os quais causam
limitações no desempenho do controle preciso, destacandose a zona morta, o atrito, histerese e a folga (backlash).
Dentro deste contexto, vários trabalhos [8, 9, 10, 11] têm
tratado da modelagem, da identificação e da compensação
da não linearidade de folga. Nordin e Gutman [8] comentam
que a folga é uma das mais importantes não linearidades que
limitam o desempenho do controle de posição e velocidade
em aplicações industriais e da robótica. A revisão
bibliográfica realizada por estes autores indica que ainda há
muita pesquisa a ser feita para síntese e análise da
compensação de folga no controle de sistemas mecânicos.
Vörös [10] apresenta uma nova forma analítica de
descrição do modelo matemático da não linearidade de folga
que utiliza funções de chaveamento e mostra os resultados
de simulação computacional da identificação dos
parâmetros.
Hägglund [11] descreve um novo método para detecção
e estimativa da não linearidade de folga em válvulas de
controle que sofreram desgaste. Ele utiliza como modelo a
função descritiva da folga e comenta que a facilidade de
compensação desta não linearidade depende de sua inversa.
Selmic e Lewis [12] apresentam um esquema de
compensação para folgas com inversão da dinâmica
utilizando a técnica do backstepping com redes neurais. Um
modelo geral da folga é usado e permite assimetria.
Cazarez-Castro et al. [13] apresenta uma combinação de
lógica fuzzy e algoritmos genéticos na busca pela solução do
problema de regulação da saída de servomecanismos com
não linearidade de folga. Os dados para simulação foram
obtidos a partir de uma bancada experimental de testes que
envolve um motor DC ligado a uma carga mecânica por
1
Proceedings of the 9th Brazilian Conference on Dynamics Control and their Applications
Serra Negra, SP - ISSN 2178-3667
214
MODELAGEM E SIMULAÇÃO COMPUTACIONAL DA NÃO LINEARIEDADE DE FOLGA EM UM ROBÔ GANTRY
Odair Menuzzi, Eduardo Padoin, Antonio Carlos Valdiero, Antonio Luis Rasia
meio de uma transmissão do tipo trem de engrenagens e
com folga.
Giri et al. [14] apresenta proposições para a
identificação de sistemas lineares com a presença da não
linearidade de folga a partir da parametrização apropriada
do sistema, a estimativa dos parâmetros pela técnica dos
mínimos quadrados e a especificação de padrões de sinais de
entrada.
Shahnazi et al. [15] propõe um controlador adaptativo
combinado com lógica fuzzy para melhorar a robustez do
controle feedback de sistemas com a presença de não
linearidades tais como sistemas mecânicos com folga no
acionamento.
Da mesma forma que Morales-Velazquez et al. [16]
propõe melhorias do controle de máquinas ferramenta com
controle numérico computadorizado (CNC) utilizando
plataformas de baixo custo e a identificação dos parâmetros
do modelo do servo sistema, o propósito deste trabalho é
apresentar uma proposta prática de modelagem matemática
e simulacão computacional dos parâmetros de folga em
transmissões mecânicas do tipo fuso (parafuso de potência)
para futura aplicação no controle e compensação de robôs
Gantry.
Este artigo se organiza de tal forma que na seção 2 é
apresentada a descrição do robô Gantry e do acionamento
tipo fuso de uma junta. A seção 3 apresenta a modelagem
matemática de uma junta robótica incluindo-se a não
linearidade de folga tal como proposta por Tao e Kokotovic
[17], na seção 5 é descrito a simulação computacional, que
contém alguns resultados numéricos obtidos no
Matlab/Simulink; e por fim apresentam-se as conclusões na
seção 6.
2. DESCRIÇÃO DO ROBÔ GANTRY E
ACIONAMENTO TIPO FUSO DE UMA JUNTA
DO
Fig. 1 – Manipulador robótico Gantry [4].
Esta seção descreve de forma sucinta o manipulador
robótico de estrutura cinemática tipo Gantry, cujo desenho
característico é mostrado na Fig. 1. O robô Gantry é
considerado o tipo de manipulador mais robusto. Tem a
cinemática mais simples entre os tipos comuns de robôs
industriais por utilizar três juntas prismáticas (J1, J2 e J3) e,
em alguns casos, uma junta rotativa (J4) para a orientação
do efetuador final (garra robótica ou ferramenta).
Um tipo de transmissão muito utilizada em juntas
prismáticas é o conjunto de fuso e porca (ou parafuso
também chamado parafuso de potência), mostrado na Fig. 2.
Este tipo de transmissão apresenta alta capacidade de carga,
sendo comum em manipuladores robóticos do tipo Gantry e
é o objeto de estudo da não linearidade de folga neste
trabalho. As transmissões de um robô têm papel muito
importante na precisão de posicionamento do manipulador,
muitas vezes é preciso reduzir ou amplificar o movimento
nos atuadores, visando-se obter a resposta desejada e
requerida na realização das tarefas programadas.
Existem diversas características não lineares na
dinâmica desses sistemas de transmissão mecânica que
dificultam o controle preciso e prejudicam seu desempenho,
entre as quais destacam-se o atrito dinâmico e a folga.
Fig. 2 – Transmissão tipo fuso utilizada no acionamento de juntas
prismáticas em manipuladores robóticos.
A Figura 3 mostra um desenho esquemático do
acionamento de uma junta prismática. O motor elétrico (1)
aplica um torque Tm no fuso (2) resultando num
deslocamento angular θm, medido por um encoder (3). Ao
girar o fuso o movimento de rotação do mesmo se converte
no deslocamento linear y de uma massa M.
2
Proceedings of the 9th Brazilian Conference on Dynamics Control and their Applications
Serra Negra, SP - ISSN 2178-3667
215
Fig. 3 – Acionamento tipo fuso de uma junta prismática do robô.
giro do fuso. O torque devido à força de reação da massa
deslocada sobre o fuso é dado por:
A não linearidade de folga acarreta fortes variações das
parcelas dinâmicas e resultam em efeitos de degradação do
desempenho do seguimento de trajetória. Na seção seguinte
apresenta-se a modelagem matemática para esta junta
robótica com a não linearidade de folga.
(4)
Da mesma forma, pode-se deduzir as equações da
dinâmica do movimento linear da massa:
3. MODELAGEM MATEMÁTICA
(5)
A formulação do modelo matemático de uma junta
prismática do robô Gantry pode ser obtida pelo método
Newton-Euler [2] a partir do equilíbrio dinâmico nos
diagramas de corpo livre do eixo-fuso e da porca-massa
deslocada. A Figura 4 mostra o diagrama de corpo livre do
eixo-fuso.
(6)
(7)
onde By é o coeficiente do atrito viscoso da massa, M é a
massa e y é o deslocamento linear da junta prismática.
Se não houvesse a imperfeição de folga no sistema
dinâmico, a relação entre o deslocamento linear da junta
prismática e o giro do eixo motor poderia ser escrita como:
(8)
Considerando o caso de não haver folga, poder-se-ia
substituir as derivadas da Eq. (8) em (7) e combinar este
resultado com a Eq. (3), resultando numa única equação
diferencial ordinária de segunda dada por:
Fig. 4 – Forças atuantes no fuso.
Pela aplicação das leis do equilíbrio dinâmico, obtem-se
as seguintes relações matemáticas:
(9)
(1)
(10)
(2)
Entretanto devido à existência da não linearidade de
folga, cada uma das equações diferenciais de segunda
ordem, Eq.s (3) e (7), não podem ser combinadas e
necessita-se de uma relação matemática que represente a
relação entre o deslocamento linear da junta, y, em função
do deslocamento angular do motor, θm , na presença da
folga. Uma revisão bibliográfica na literatura recente [8, 9,
(3)
é o torque motor, J é o momento de inércia de todo
onde
conjunto em rotação (fuso e eixo motor), Bθ é o coeficiente
do atrito viscoso do eixo, p é o passo do fuso, Fu é a força de
reação da massa deslocada sobre o fuso, m é o ângulo de
3
Proceedings of the 9th Brazilian Conference on Dynamics Control and their Applications
Serra Negra, SP - ISSN 2178-3667
216
MODELAGEM E SIMULAÇÃO COMPUTACIONAL DA NÃO LINEARIEDADE DE FOLGA EM UM ROBÔ GANTRY
Odair Menuzzi, Eduardo Padoin, Antonio Carlos Valdiero, Antonio Luis Rasia
10, 11, 12, 13, 14, 15, 17, 18], que trata da não linearidade
de folga, permitiu a formulação desta relação matemática
para a transmissão tipo fuso. Adaptando-se o modelo
proposto por Tao e Kokotovic [17], descreve-se a folga a
partir das seguintes equações:
4.
RESULTADOS
COMPUTACIONAL
DE
SIMULAÇÃO
Esta seção apresenta uma descrição detalhada da
metodologia utilizada na implementação da simulação
computacional do modelo matemático para uma junta
prismática de um robô Gantry com a presença da não
linearidade de folga, os parâmetros adotados para o sistema
e os resultados de simulação.
A simulação numérica do modelo proposto foi
implementada com o auxílio da ferramenta computacional
MatLab/Simulink, utilizando-se o método de integração
Runge-Kuta com passo de 0,0001 segundos..
Os parâmetros do modelo matemático da folga, descrito
pela Eq. (11), e utilizados nas simulações computacionais
foram determinados a partir de uma bancada experimental e
estão apresentados na Tab. 1.
(11)
onde m é a relação de transmissão, cl e cr são constantes, e vl
e vr são funções de projeções dadas pela equação (12).
(12)
A Figura 5 mostra um desenho esquemático da não
linearidade de folga e a representação gráfica do modelo
matemático dado pela Eq. (11).
Tabela 1- Parâmetros do modelo da folga obtidos de uma bancada
experimental.
Descrição dos Parâmetros
Passo do fuso p
Relação de transmissão m
Intervalo de folga à direita cr
Intervalo de folga à esquerda cl
Entrada posição angular θm
Posição inicial da carga y(t=0)
Valores
5 mm = 5 x 10-3 m
7,957 x 10-4 m/rad
1,57 rad
-1,57 rad
variando
1,25 x 10-3 m
Inicialmente foi realizada apenas a simulação do modelo
de folga, dado pela Eq. (11) e implementado por meio do
diagrama de blocos apresentado na Fig. 6, com interesse de
observar as características da não linearidade de folga da
saída do movimento (y) em relação às posições de entrada
(θm).
Fig. 5 – Não linearidade da folga: desenho esquemático e representação
gráfica do modelo proposto.
Fig. 6 – Diagrama de Blocos do modelo matemático da não linearidade de folga para uma transmissão tipo fuso.
4
Proceedings of the 9th Brazilian Conference on Dynamics Control and their Applications
Serra Negra, SP - ISSN 2178-3667
217
A Figura 7 é resultado da simulação computacional do
modelo matemático implementado no diagrama de blocos da
Fig. 6 sob às condições iniciais e parâmetros da Tab. 1.
Em seguida foram realizadas as simulações
computacionais do diagrama de blocos da Fig. 8 que
representa o acionamento de uma junta prismática tipo fuso
de um robô Gantry. Neste diagrama de blocos foram
implementadas as equações (9), (10) e (11). Na simulação
computacional foram utilizados os parâmetros da folga,
dados pela Tab. 1, e do braço robótico, dados pela Tab. 2.
15
teta(rad)
y(m)*1e3: sem folga
y(m)*1e3: com folga
erro(m)*1e3
10
Tabela 2- Parâmetros do Robô Gantry considerando o movimento de
uma junta prismática.
5
Descrição dos Parâmetros
Momento de Inércia do eixo
motor J
Massa da carga M
Coeficiente de amortecimento
viscoso do eixo motor Bo
Coeficiente de amortecimento
viscoso da massa By
Torque do motor Tm
0
-5
-10
-15
0
2
4
6
8
Tempo (s)
10
12
14
16
Valores
9,331 x 10-5 kg.m2
0,5 kg
1 N.m.s
1 N.s/m
Variando linearmente
e de forma alternada
Fig. 7 – Resultado de simulação computacional do modelo da folga.
Fig. 8 – Diagrama de Blocos do modelo dinâmico de uma junta prismática de um robô Grantry com a não linaeridade de folga.
5
Proceedings of the 9th Brazilian Conference on Dynamics Control and their Applications
Serra Negra, SP - ISSN 2178-3667
218
MODELAGEM E SIMULAÇÃO COMPUTACIONAL DA NÃO LINEARIEDADE DE FOLGA EM UM ROBÔ GANTRY
Odair Menuzzi, Eduardo Padoin, Antonio Carlos Valdiero, Antonio Luis Rasia
Os resultados numéricos da simulação dos movimentos
da junta robótica são apresentados na forma do gráfico da
Fig. 9.
teóricos a partir de modelos ideais, havendo uma lacuna
para pesquisa a partir da observação e validação
experimental com compensação da folga e minimização de
seus efeitos.
teta(rad)
y(m)*1e3: sem folga
y(m)*1e3: com folga
erro(m)*1e3
20
15
AGRADECIMENTOS
Os autores são agradecidos à UNIJUÍ pela estrutura
laboratorial disponível e às diversas agências que tem
apoiado finaceiramente a pesquisa, tais como a FAPERGS,
FINEP/MCT, SEBRAE, CNPq e CAPES.
10
5
0
REREFÊNCIAS
-5
[1] D. V. Hunt, “Industrial Robotics Handbook”, Industrial
Press, pag. 427, New York, 1983.
[2] L. Sciavicco and B. Siciliano, “Modeling And Control
of Robot Manipulators”, McGraw-Hill, Naples, 1996.
[3] A. Cupido, R. Sala and S. Milanesi, “Sistemi Ed
Automazione Industriale”, Vol. 3, Bologna, 1996.
[4] S. Paatz, “Anatomy of a Robot”, Engineering &
Technology, p. 42-44, 2008.
[5] P. J. Turner, P. Nigrowsky and P. Vines, “A New
Approach for the Design of Robot Joint Transmission”,
Mechatronics, 2001.
[6] F. Ross, H. Johansson and J. Wikander, “Optimal
selection of motor and gearhead in mechatronic
applications”, Mechatronics, p. 63-72, 2006.
[7] A. C. Valdiero, "Hydraulic Robot Control with Friction
Compensation" (In Portuguese), PhD Thesis,
Mechanical
Engineering
Department,
Federal
University of Santa Catarina, Brazil, 2005.
[8] M. Nordin and P. O. Gutman, “Controlling mechanical
systems with backlash _ A survey”, Automatica,
38(10), p. 1633-1649, 2002.
[9] R. Dong and Y. Tan, Y., “A Gradient Based Recursive
Identification of Mechanical Systems with Backlashlike Hysteresis”; 18th IEEE International Conference on
Control Applications Part of 2009 IEEE Multiconference on Systems and Control Saint Petersburg,
Russia, 2009.
[10] J. Vörös, “Modeling and identification of systems with
backlash”, Automatica, 2009.
[11] T. Hägglund, T., “Automatic on-line estimation of
backlash in control loops”, Journal of Process Control,
17(6), p. 489-499, 2007.
[12] R. R. Selmic and F. L. Lewis, “Neural net backlash
compensation with Hebbian tuning using dynamic
inversion”, Automatica, Vol. 37, p. 1269-1277, 2001.
[13] N. R. Cazares-Castro, L. Aguilar and O. Castilho,
“Fuzzy Logic Control with Genetic Membership
Function Parameters Optimization for the Output
Regulation of a Servomechanism with Nonlinear
Backlash”, Expert Systems with Applications, p. 3-6,
2009.
[14] F. Giri, Y. Rochdi, F. Z. Chaoui and A. Brouri,
“Identification of Hammerstein systems in presence of
hysteresis-backlash and hysteresis-relay nonlinearities”,
Automatica, p. 2-7, 2008.
[15] R. Shahnazi, N. Pariz and A. V. Kamyad, “Adaptive
fuzzy output feedback control for a class of uncertain
-10
-15
-20
0
2
4
6
8
Tempo (s)
10
12
14
16
Fig. 9– Resultado de simulação computacional do modelo matemático
da junta prismática do robô Gantry incluindo-se a não linearidade da
folga.
Os resultados mostrados nas figuras 7 e 9 permitem a
observação de algumas características importantes da não
linearidade de folga. Note que diante da periocidade da
entrada (θm), a saída do movimento (y) apresenta as
características fundamentais de atraso de fase e de perda de
movimento nos trechos de pico da entrada.
Diante dos resultados destas simulações do sistema
dinâmico em malha aberta, percebe-se a importância da
modelagem matemática e da identificação da folga em
transmissões mecânicas. O conhecimento das características
desta não linearidade nos sistemas mecânicos permite a
elaboração de esquemas de compensação nas estratégias de
controle e consequentemente a melhoria do desempenho nas
tarefas industriais que exigem precisão e repetibilidade.
5. CONCLUSÃO
Neste trabalho foram apresentadas a modelagem
matemática e as simulações computacionais do acionamento
de uma junta prismática de um robô tipo Gantry, onde
ocorre a presença da não linearidade de folga. Desenvolveuse o modelo matemático da junta robótica incluindo-se a não
linearidade de folga.
Os testes e simulações computacionais mostrados neste
trabalho ilustram o comportamento da não linearidade de
folga e suas principais características, tais como o erro de
seguimento de posição, o atraso de fase e a perda de
movimento nas inversões de velocidade. Os resultados
demonstram a importância da compensação da folga,
ressaltando os aspectos de desempenho do posicionamento.
Como perspectivas futuras, pretende-se realizar os testes
experimentais do protótipo de uma junta prismática tipo
fuso na bancada disponível na UNIJUÍ Campus Panambi e
estudar um procedimento de identificação desta não
linearidade com base nos trabalhos apresentados na
literatura internacional recente [9, 10, 11, 13, 14, 17, 18].
Entretanto estes trabalhos apresentam apenas resultados
6
Proceedings of the 9th Brazilian Conference on Dynamics Control and their Applications
Serra Negra, SP - ISSN 2178-3667
219
nonlinear systems with unknown backlash-like
hysteresis”, Commun Nonlinear Sci Numer Simulat, p.
6-10, 2009.
[16] L. Morales-Velazquez, R. J. Romero-Troncoso, R. A.
Osornio-Rios, G. Herrera-Ruiz and J. J. Santiago-Perez,
“Special purpose processor for parameter identification
of CNC second order servo systems on a low-cost
FPGA platform”, Mechatronics, 2009.
[17] G. Tao and P. V. Kokotovic, “Adaptative control of
systems with actuator and sensor nonlinearities”, John
Wiley & Sons, p. 294, New York, 1996.
[18] R. Dong, Y. Yonghong, 2009, “A Gradient Based
Recursive Identification of Mechanical Systems with
Backlash-like Hysteresis”; 18th IEEE International
Conference on Control Applications Part of 2009 IEEE
Multi-conference on Systems and Control Saint
Petersburg, Russia.
7
Proceedings of the 9th Brazilian Conference on Dynamics Control and their Applications
Serra Negra, SP - ISSN 2178-3667
220