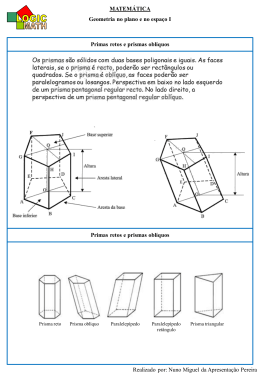
1
SÍNTESE DE CONTEÚDO – MATEMÁTICA
SEGUNDA SÉRIE - ENSINO MÉDIO
ASSUNTO : OS PRISMAS
NOME : ..............................................NÚMERO : ...... TURMA :.......
============================================================
OS PRISMAS
1) Conceito :
Dados dois planos paralelos α e β , um polígono convexo qualquer
contido em β e uma reta r concorrente com α e β , chamamos de
PRISMA o conjunto de todos os segmentos de reta paralelos a r , com
uma extremidade pertencente ao polígono e outra pertencente a α .
Exemplo :
Na figura abaixo , o polígono considerado , pertencente a β é um
pentágono . Observe como será a figura resultante : Parece uma caixa ,
é um prisma pentagonal .
2
Outros exemplos de prismas :
2) Elementos dos prismas :
Tomemos como exemplo o prisma abaixo para definirmos os elementos principais dos prismas em geral :
a) As bases são os dois polígonos congruentes contidos nos planos
paralelos que geraram o prisma : ABCDEF e A’B’C’D’E’F’ (hexágonos) .
3
b) As arestas são todos os segmentos que limitam o prisma . Então ,
temos arestas da base (AB , BC , CD , DE , EF , FA e A’B’ ,
B’C’ , C’D’ , D’E’ , E’F’ , F’A’ ) e as arestas laterais ( AA’ ,
BB’ , CC’ , DD’ , EE’ e FF’ ) .
c) Os vértices são todos os pontos onde as arestas se cruzam , ou seja
A , B , C , D , E , F , A’, B’, C’ , D’, E’ e F’ .
d) A altura é a distância entre as bases .
e) As faces laterais são os paralelogramos que têm como lados
opostos duas arestas das bases e duas arestas laterais . No nosso
caso : ABB’A’ , BCC’B’ , CDD’C’ , DEE’D’ , EFF’E’ e FAA’F’.
3) Classificação dos Prismas :
→ Se as arestas laterais de um prisma são perpendiculares aos planos das bases , então esse prisma é RETO . Se as arestas laterais
não são perpendiculares aos planos das bases , então o prisma é
INCLINADO ou OBLÍQUO .
Exemplos :
4
→ Um prisma é REGULAR quando é reto e tem base regular
( O que significa ter base regular ? ) :
Exemplos :
4) Prismas Notáveis : O paralelepípedo e o Cubo
a) O prisma cujas faces são paralelogramos é chamado de Paralelepípedo .
Exemplos :
5
b) Se num paralelepípedo todas as faces são quadradas , então esse paralelepípedo é um Cubo .
5) Cálculo da diagonal do paralelepípedo :
Observe que na figura temos um paralelepípedo cujo
comprimento ,largura e altura medem, respectivamente a ,
b e c , a diagonal do paralelepípedo mede D e digamos
que a diagonal da base inferior mede x . Então , temos pelo
teorema de pitágoras :
D2 = x2 + c2 , mas também x2 = a2 + b2 . Então , temos
D2 = a2 + b2 + c2 e , finalmente : D = a 2 + b 2 + c 2
6
Para o cubo teremos a = b = c
:
E como o cubo é um paralelepípedo , temos :
AG =
a2 + a2 + a2 =
3a 2 = a 3
Exemplos :
a) Calcule a diagonal do paralelepípedo mostrado na figura a seguir ,
Considerando que as medidas são dadas em metros :
Resolução :
Como a = 4 m , b = 3 m e c = 2 m , temos :
D=
(4) 2 + (3) 2 + (2) 2 =
16 + 9 + 4 = 29 m
b) Calcule a aresta de um cubo e a diagonal de uma de suas faces ,
sabendo que sua diagonal mede 75 cm .
7
Resolução :
Consideremos que a medida da aresta do cubo é a , a diagonal da face inferior é d1 e a diagonal do cubo é d = 75 cm . Então temos :
75 75 3
a) a 3 = 75 . Então a =
=
= 25 3 cm .
3
3
b) Aplicando o teorema de Pitágoras ao triângulo ABD :
d1 = a 2 + a 2 = 2a 2 Então d1 = a 2 = 25 3 . 2 = 25 6 cm
2
6) Áreas relacionadas aos prismas :
a) Área da base : É a área do polígono que representa a base .
Exemplos :
1) Se um prisma tem base triangular com as arestas da base medindo 2 cm , 5 cm e 6 cm , calcule a área da base do prisma .
5
2
6
A base é irregular , mas como as arestas
são conhecidas , podemos usar a fórmula
de Heron , vista no último trabalho :
Seja A b a área da base . Como o semi2 + 5 + 6 13
perímetro da base é p =
= cm ,
2
2
13 13
13
13
Temos : ( Ab)2 =
( − 2)( − 5)( − 6)
2 2
2
2
3 39
e Ab =
cm 2
4
8
2) Se um prisma regular tem base hexagonal com arestas da base
medindo 2 cm , então calcule a área da base desse prisma .
2 cm
Como a área do hexagono regular é dada em
função do lado pela fórmula já conhecida
3a 2 3
Ahex =
, temos no caso do prisma :
2
3(2) 2 3
Ab =
= 6 3 cm 2
2
b) Área Lateral :
Você já deve ter percebido que :
⇒ As faces laterais de um prisma oblíquo são paralelogramos , e
⇒ As faces laterais de um prisma reto são retângulos .
paralelogramo
retângulo
Então :
- No prisma reto : Área de uma face = Área de retângulo .
- No prisma oblíquo : Área de uma face = Área de paralelogramo
9
Área lateral de um prisma é a soma das áreas de todas as faces
laterais do prisma .
Exemplos :
1) A figura abaixo mostra um prisma hexagonal regular com aresta
com aresta da base medindo
= 8 cm e altura h = 10 cm .
Calcule a área da base e a área lateral do prisma .
→ A base é mostrada na figura da direita . Sua área é
3(8) 2 3
Ab =
= 96 3 cm 2
2
→ Como o prisma é regu –
lar , cada uma de suas faces
laterais é um retângulo xh
e tem área = 8.10 = 80 cm2.
Logo , como são 6 faces laterais , AL = 6. 80 =480cm2.
.
2) Calcule a área lateral do paralelepípedo mostrado na figura a
seguir , sabendo que o comprimento é o quíntuplo da altura , a
largura é o dobro da altura e a diagonal mede 2 30 cm .
a)Cálculo das dimensões do paralelogramo :Como a diagonal foi dada , te -
P
x
2x
Q
5x
mos: 2 30 = (5 x ) 2 + (2 x) 2 + ( x ) 2
Elevando ambos os lados ao quadrado ,
temos 120 = 30x2 de onde x = 2 cm .As
dimensões do paralelogramo são 10 cm ,
4cm e 2 cm .
b) Cálculo da área lateral do paralelepípedo : A área lateral compreende :
2 retângulos 10x2 e 2 retângulos 4x2 .
Então : AL= 2.10.2 + 2.4.2 = 40 + 16 =
= 56 cm2 .
10
c) Área total do prisma :
É a soma das áreas das bases com a área lateral . Então , temos :
AT = AL + 2. Ab
Exemplo : Calcule a área total do prisma reto abaixo .
1) Como a base é um triângulo retângulo isósceles ,
temos : (3 2 ) 2 = a2 + a2 ⇒ a 2 = 9 e a = 3 cm .
3.3
9
2) A b =
=
cm .
2
2
3) AL = 2. ( 3 . 6) + ( 3 2 . 6) = 36 + 18 2 cm2.
9
4) AT = AL + 2. Ab = (36 + 18 2 ) + 2. =
2
2
= 45 + 18 2 = 9( 5 + 2 2 ) cm .
EM ALGUNS CASOS ESPECIAIS
É POSSÍVEL CRIAR FÓRMULAS
GERAIS !
VEJA !
1) Se o prisma é regular com aresta da base a e altura h , podemos
ter : AL = n . ah e AT = n.ah + 2. Ab , onde n é o número de
arestas da base .
11
2) Num paralelepípedo retângulo , em geral , temos as dimensões indicadas na figura abaixo . Então vale a fórmula :
c
AT = 2.(ab + ac + bc)
b
a
3) No cubo , temos 6 faces quadradas e congruentes com arestas
de medida a . Vale então a fórmula :
AT = 6a2
a
a
a
12
7) VOLUME DOS PRISMAS :
A secção transversal de um prisma é a intersecção não vazia , desse prisma com qualquer plano , paralelo às suas bases . Veja figura :
Num prisma , todas as secções transversais têm mesma área já que
todas as secções transversais são paralelas às bases e as arestas laterais
são paralelas entre sí . Isso significa que , se você empilhar várias porções congruentes do plano , terá um sólido de volume equivalente às
áreas de todas as porções juntas , no caso do prisma , a área de um polígono várias vezes . Em outras palavras , podemos fatiar um prisma em
prismas congruentes de altura unitária :
13
Como todas as fatias têm altura unitária , e todas elas têm a mesma
área que é Ab , podemos enunciar o seguinte :
O VOLUME DE UM PRISMA É O PRODUTO
DA ÁREA DE SUA BASE POR SUA ALTURA*
*A
altura do prisma é a soma das alturas unitárias dos prismas menores (fatias) .
Em linguagem matemática teremos :
VPRISMA = Ab . h
Exemplos :
1) Calcule a área total e o volume do paralelepípedo retângulo
da figura a seguir : ( medidas dadas em cm )
A
B
D
C
13
E
F
5
H
3
G
Resolução :
a) O triângulo EGH é retângulo em H . Então :
(5)2 = (3)2 + (EH)2 , de onde sai que EH = 4 cm
b) O triângulo AEG é retângulo em E . Então :
(13)2 = (5)2 + (AE)2 , de onde sai que AE = 12 cm
c) AT = 2.( 3.4 + 3.12 + 4.12) = 192 cm2
d) V = Ab . h = 3.4.12 = 144 cm3
2) Na figura seguinte , a base do prisma regular está inscrito
na circunferência de perímetro igual 6π cm . Se a altura do
prisma é igual a 8 cm , calcule seu volume .
14
Resolução :
Sabemos que o perímetro de uma circunferência de raio r é igual a 2π
πr que ,
neste caso , é igual a 6π . Então : 2π = 6π , de onde
= 3 cm
Como a base é um hexágono regular , temos : A b =
Logo
V = Ab . h =
3(3) 2 3 27 3
cm 2
=
2
2
27 3
. 8 = 108 3 cm 3
2
3) Se a diagonal de um cubo mede 6 dm , calcule sua área total
e seu volume .
Resolução :
6 dm
a
a
Sabemos que a diagonal de um cubo com aresta a é
a 3 . Então temos a 3 = 6 ⇒ a = 2 3 dm
e teremos ainda :
a) AT = 6 . (2 3 ) 2 = 72 dm 2
b) V = Ab . h = a .a . a = a3 = (2 3 ) 3 = 24 3 dm3
a
AQUI TAMBÉM É
POSSÍVEL CRIAR
FÓRMULAS PARA OS
PARALELEPÍPEDOS
→ Como , nos paralelepípedos de dimensões a , b e c , a base pode
ter área ab , bc ou ac com alturas c , a ou b , respectiva –
mente , podemos registrar :
Vparal = abc
→ Então , para os cubos de aresta a , teremos
Vcubo = a3
15