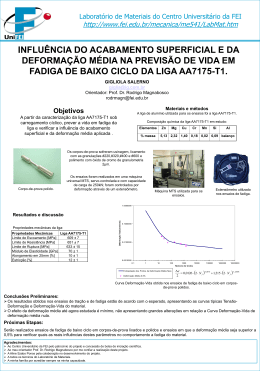
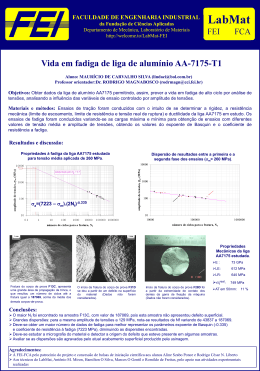
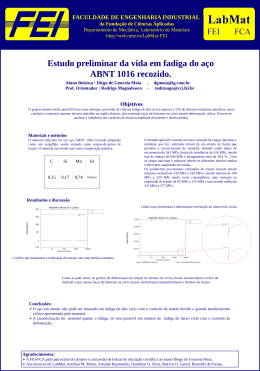
INFLUÊNCIA DA DEFORMAÇÃO MÉDIA NA
PREVISÃO DE VIDA EM FADIGA DE BAIXO
CICLO DA LIGA AA7175-T1.
www.fei.edu.br
AUTORA : Gigliola Salerno ([email protected])
Orientador: Prof. Dr. Rodrigo Magnabosco ([email protected])
Departamento de Engenharia Mecânica
Ensaios de Fadiga:
Introdução
Um material pode falhar sob esforços cíclicos com tensão abaixo
da máxima que suportaria em um carregamento estático. Este
processo é definido como fadiga.
Objetivos
A partir da caracterização da liga de alumínio AA7175-T1 sob
carregamento cíclico, prever a vida em fadiga desta liga,
verificando também a influência da deformação média aplicada.
Materiais e métodos
Composição química da liga AA7175-T1 em estudo.
Elemento Zn
Mg
Cu
Cr
Mn
Si
Al
Curva Amplitude de Deformação por Número de Ciclos a Fratura para
Deformação Média Nula.
800
Propriedades Mecânicas
Liga AA7175-T1
Expoente de Encruamento Cíclico, n’
0,038
Coeficiente de Resistência Cíclico, H’ [MPa]
783
Coeficiente de Resistência a Fadiga, σ'f [MPa]
814
Expoente de Resistência a Fadiga, b
-0,059
Coeficiente de Ductilidade a Fadiga, εf’
0,670
Expoente de Ductilidade a Fadiga, c
-1,184
[mm/mm]
Tensão Real [MPa]
Em corpos-de-prova da liga de alumínio AA7175-T1 foram
realizados ensaios de tração e de fadiga em uma máquina
universal de ensaios MTS com capacidade de carga de 250kN,
utilizando extensômetro de 25 mm de curso útil.
600
400
200
Monotônica
Cíclica
0,03
0,04
0
0
% massa 5,13 2,32 1,40 0,18 0,02 0,09 balanço
0,1
y = 0,295x-1,184
y = 0,011x
-0,059
y = 0,013x
-0,103
y = 0,012x
-0,065
y = 0,018x
-0,137
0,02
y = 0,005x
y = 0,342x-1,173
0,008
0,006
0,05
y = 0,004x-0,726
0,01
0,001
0,0001
0,00001
0,004
0,000001
1
10
100
1000
10000
1
10
100
Número de Ciclos a Fratura
Número de Ciclos a Fratura
Nula
Potência (Nula)
Extensômetro.
y = 0,642x-1,260
y = 0,476x-1,212
-0,006
Amplitude de Deformação Plástica
[mm/mm]
Amplitude de Deformção Elástica
[mm/mm]
0,01
Corpo-de-prova.
0,01
Deformação Real Uniforme [mm/mm]
0,5%
Potência (0,5%)
1,0%
Potência (1,0%)
1,5%
Potência (1,5%)
Nula
Potência (Nula)
2,00%
Potência (2,00%)
0,50%
Potência (0,50%)
1,00%
Potência (1,00%)
1000
1,50%
Potência (1,50%)
10000
2,00%
Potência (2,00%)
Curvas Amplitude de Deformação por Número de Ciclos a Fratura para
Deformação Média Diferente de Zero.
10000
Máquina universal de
ensaios MTS.
Estes corpos-de-prova foram usinados, lixados por lixas de
granulações: #80, #220, #320, #400 e #600 e polidos com óxido
de cromo de granulometria 2μm.
Rugosidade superficial dos corpos-de-prova após polimento.
segundo a norma JIS 1994.
1000
100
10
100
1000
Número de Ciclos até a Fratura
Transversal (µm) Longitudinal (µm)
0,50%
0,0350,015
0,0380,018
máxa E  662.5962Nf 
Tensão [MPa]
Módulo de Elasticidade, E [GPa]
71±1,8
700
Limite de Escoamento, σLE [MPa]
611±6,5
600
Limite de Resistência, σLR [MPa]
656±9,7
500
638±15
400
Limite de Ruptura, σf [MPa]
~
Tensão Real de Ruptura, f
300
Alongamento em 25 mm [%]
200
Estricção, RA [%]
100
Deformação Real de Ruptura,
[MPa]
0
0.05
Deformação [mm/mm]
0.06
0.07
0.08
13,2±2,5
f
[mm/mm]
0,142±0,025
Expoente de Encruamento, n
0,069
Coeficiente de Resistência, H
869
~
Deformação Real Uniforme,
Agradecimentos:
735±4,3
10±1,3
~
0.04
2%
 38.721.9802Nf 
1, 243
AA7175-T1
800
0.03
1,50%
Equação obtida pelo parâmetro SWT, que descreve o comportamento em
fadiga de baixo ciclo para a liga.
Propriedades Mecânicas
0.02
1%
0,118
Ensaios de Tração:
0.01
Nula
Curva obtida pelo parâmetro SWT
Resultados e discussão
0
10000
u
0,058±0,0085
Conclusões:
A liga apresenta comportamento misto (endurecimento e
amolecimento cíclico).
Os dados monotônicos não podem ser extrapolados para prever
a vida em fadiga deste material.
Os valores de b,c,f’ e f’ variam conforme a deformação média,
portanto a relação linear da equação de Morrow não é válida.
 A equação SWT é válida como parâmetro para determinar a
vida em fadiga do material independente da deformação média
aplicada.
 Ao Centro Universitário da FEI pelo patrocínio do projeto e concessão de bolsa de iniciação científica a aluna Gigliola Salerno.
 Ao meu orientador Dr. Rodrigo Magnabosco.
 A minha família.