ÁLGEBRA LINEAR ALGORÍTMICA
ESTUDOS DIRIGIDOS 2014
1
2
ESTUDOS DIRIGIDOS 2014
E STUDO DIRIGIDO 1
C ÔNICAS
Objetivo: obter as equações cartesianas da hipérbole a partir de sua definição como lugar
plano.
1. Originalmente as cônicas foram definidas pelos matemáticos gregos como as curvas
obtidas quando um cone reto é cortado por um plano. Neste curso vamos tomar como
ponto de partida para o estudo destas curvas as suas definições como lugares geométricos
planos, também descobertas pelos matemáticos da Grécia Antiga. Um lugar geométrico é
o conjunto de todos os pontos do plano que satisfazem uma determinada propriedade. Por
exemplo, uma circunferência é o lugar geométrico dos pontos do plano que são equidistantes de um ponto fixo, que chamamos de centro da circunferância. As cônicas podem ser
definidas como lugares geométricos da seguinte maneira:
Elipse: é o lugar geométrico dos pontos do plano cuja soma das distâncias a dois
pontos fixos é constante.
Hipérbole: é o lugar geométrico dos pontos do plano cuja diferença entre as distâncias a dois pontos fixos é constante.
Parábola: é o lugar geométrico dos pontos do plano que são equidistantes de um
ponto fixo e de uma reta fixa.
Os pontos fixos a que se referem as definições da elipse e da hipérbole são chamados de
focos. Já no caso da parábola, temos um ponto fixo, também chamado de foco, e uma
reta, conhecida como diretriz da parábola. Neste estudo dirigido vamos nos concentrar em
estudar as propriedades da hipérbole, as duas outras cônicas são tratadas em detalhe nas
notas de aula.
2. Para começar queremos determinar a equação cartesiana da hipérbole. Para isto precisamos fixar um sistema de eixos. Vamos escolhê-los da seguinte maneira:
• o eixo das abscissas será a reta que passa pelos dois focos;
• o eixo o das ordenadas será a reta que que passa no meio dos dois focos.
A orientação dos eixos é indiferente: a equação não é afetada pela orientação escolhida.
Como a origem, por construção, fica no ponto médio entre os focos, teremos que F1 =
[−c, 0]t e F2 = [c, 0]t , sob a identificação habitual entre um ponto e o vetor que vai da
origem a este ponto. Para que P = [x, y]t seja um ponto da hipérbole, deveremos ter que
(1)
kP − F2 k − kP − F1 k = ±d,
ÁLGEBRA LINEAR ALGORÍTMICA
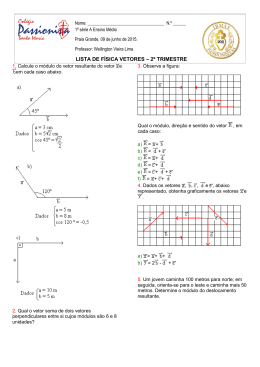
3
P
F1
F2
em que d é um número real fixo. Note que escrevemos ±d e não d porque não sabemos
qual é a maior das duas distâncias entre P e os focos. Levando em conta as coordenadas
de F1 , F2 e P , temos que
p
p
∆1 = kP − F1 k = (x − c)2 + y 2 e ∆2 = kP − F2 k = (x + c)2 + y 2
Assim, (1) pode ser escrito na forma ∆2 − ∆1 = ±d, que, elevado ao quadrado, nos dá
(2)
∆22 + ∆21 − 2∆1 ∆2 = d2 .
Para chegar à equação desejada, siga o seguinte roteiro:
Etapa 1: Supondo que a curva corta o eixo dos x nos pontos [±a, 0]t , verifique que
d = 2a e substitua este valor em (2).
Etapa 2: Calcule, separadamente, ∆22 , ∆21 e ∆1 ∆2 , substitua em (2) e simplique.
Etapa 3: Reescreva a expressão resultante da Etapa 2 como um radical igual a uma
expressão sem radical, eleve ambos os membros ao quadrado e simplifique.
Etapa 4: Ponha em evidência x2 e y 2 do lado esquerdo da equação e mova os termos
constantes para o lado direito.
Etapa 5: Substitua c2 − a2 por b2 no coeficiente de x2 e no termo constante.
Etapa 6: Dividindo toda a equação por a2 b2 você deve obter
x2 y 2
− 2 =1
a2
b
Como neste curso estamos permitindo apenas números reais, precisamos que c2 −a2 ≥ 0 para
poder escrevê-lo como o quadrado de um número na Etapa 6. Explique, a partir da definição
geométrica da hipérbole, porque c2 − a2 ≥ 0.

4
ESTUDOS DIRIGIDOS 2014
E STUDO DIRIGIDO 2
C LASSIFICAÇÃO DE CÔNICAS
Objetivo: determinar a qual das cônicas corresponde uma dada equação quadrática em
duas variáveis.
Neste estudo dirigido consideraremos apenas equações de grau dois sem termos lineares. A
presença de termos lineares indica ou que se trata de uma parábola, ou que a curva não tem
centro na origem, caso em que seria necessário efetuar uma translação, que não é uma transformação linear e, portanto, está fora do escopo deste curso.

1. Tendo em vista a observação acima, a equação de grau dois mais geral que consideraremos neste curso é da forma
(3)
ax2 + bxy + cy 2 + d = 0,
em que a, b, c, d ∈ R.
O polinômio de grau dois em duas variáveis ax2 +bxy+cy 2 é chamado de forma quadrática
e podemos escrevê-lo em forma matricial como v t Av, em que v = [x, y]t é um vetor cujas
entradas são as variáveis x e y e A é a matriz simétrica
"
#
a b/2
(4)
A=
b/2 c
que chamaremos de matriz associada à forma quadrática ax2 + bxy + cy 2 .
√
2
Exercício
1.
Determine
as
matrizes
associadas
às
formas
quadráticas
3x
+2
2xy +4y 2 ,
√
2
2
2
2
3x + 2 3xy + 5y
e x + 4xy − 2y .
2. A forma canônica das formas quadráticas associadas à elipse e à hipérbole podem ambas
ser escritas como
(
λ1 = 1/a2 e λ2 = 1/b2
para a elipse
λ1 x2 + λ2 y 2 em que
2
2
λ1 = 1/a e λ2 = −1/b para a hipérbole
Nosso objetivo é encontrar uma rotação que, aplicada à forma quadrática v t Av, transformea em sua forma canônica. Se a matriz que descreve esta rotação for Q, então devemos
ter v = Qv1 , em que v1 = [x1 , y1 ]t . Como a matriz associada a λ1 x21 + λ2 y12 é D =
diag(λ1 , λ2 ), desejamos obter Q de modo que
v t Av = (Qv1 )t A(Qv1 ) = v1t Qt AQv1 = v1t Dv1 , o que acontece se, e só se, Qt AQ = D.
Na aula anterior vimos que λ1 e λ2 são raízes, também conhecidas como autovalores, da
equação do segundo grau na variável t definida por
det(A − tI) = 0,
que é chamada de equação característica de A.
ÁLGEBRA LINEAR ALGORÍTMICA
5
Exercício 2. Calcule os autovalores das matrizes associadas às formas quadráticas do
Exercício 1 e determine a forma canônica de cada uma delas.

Note que a equação característica nos permite achar os autovalores de A sem jamais determinar qual é a rotação Q.
Exercício 3. Calcule a equação característica da matriz A definida em (4) em função de
a, b e c. Mostre que esta equação sempre tem raízes reais.
3. Finalmente, precisamos da rotação Q. Mas
Qt AQ = D = diag(λ1 , λ2 ),
de modo que
Qt AQe1 = De1 = λ1 e1 .
Multiplicando esta última equação à esquerda por Q, obtemos
AQe1 = λ1 Qe1 ;
isto é
(A − λ1 I)Qe1 = 0.
Em outras palavras, a primeira coluna (= Qe1 ) de Q é um vetor unitário u que satisfaz
(A − λ1 I)u = 0.
Exercício 4. Determine a segunda coluna de Q, quando sua primeira coluna for [c, s]t .
Exercício 5. Determine as matrizes de rotação que transformam cada uma das formas
quadráticas do Exercício 1 nas correspondentes formas canônicas.
Exercício 6. A matriz simétrica definida em (4) não é a única matriz que nos permite
escrever a forma quadrática ax2 + bxy + cy 2 em forma matricial. Por exemplo,
"
#" #
h
i a b x
v t Bv = x y
= ax2 + bxy + cy 2 .
0 c y
| {z }
B
Calcule a matriz B, definida acima, quando a forma quadrática é x2 +xy +y 2 , encontre os
seus autovalores e determine qual deveria ser a rotação correspondente. Explique porque
a resposta obtida não pode estar certa.
O problema do exercício 5 ocorre porque o procedimento que estudamos neste estudo dirigido
só funciona corretamente quando a matriz é simétrica. Para entender a razão disso teremos
que esperar até o final do curso.

6
ESTUDOS DIRIGIDOS 2014
E STUDO DIRIGIDO 3
O PERADORES ORTOGONAIS NO PLANO
Objetivo: caracterizar os possíveis operadores ortogonais no plano.
1. Seja R uma reflexão do plano cujo espelho é a reta r e seja v 6= 0 um vetor qualquer
do plano. Mostre como calcular um vetor diretor da reta a partir de v e R(v). Você deve
saber justificar sua resposta a partir das propriedades geométricas da reflexão. Esboçar um
desenho com as posições da reta r e dos vetores v e R(v) dá uma ideia de como achar o
vetor diretor.
2. Determine o espelho e a matriz da reflexão R do plano que satisfaz:
R([1, 3]t ) = −
1
[241, 477]t .
169
√
t
3. Determine
a
matriz
da
rotação
ρ
que
leva
o
vetor
v
=
[1,
2]
no
vetor
[(−4
2+
√
t
1)/3, (2 2 + 2)/3] . Qual o ângulo desta rotação? Ela é horária ou anti-horária?
4. Mostre que se T é um operador ortogonal, então hT (v)|T (w)i = hv|wi e kT (v)k = kvk
para todo vetor v do plano.
5. Determine quais das afirmações abaixo são verdadeiras e quais são falsas. Justifique
cuidadosamente suas respostas.
(a) existe uma rotação que leva o vetor [2, 1]t no vetor [3, 1]t ;
(b) existe uma rotação que leva [2, 1]t em [1, 2]t ;
(c) existe uma reflexão que leva o vetor [2, 1]t no vetor [3, 1]t .
6. Sejam Q uma matriz 2 × 2 e I a matriz identidade 2 × 2. Mostre que as seguintes
afirmações são equivalentes:
(a) Qt Q = I;
(b) os vetores Q(:, 1) e Q(:, 2) são unitários e ortogonais entre si.
ÁLGEBRA LINEAR ALGORÍTMICA
7
Dizemos que uma matriz que satisfaz as propriedades acima é ortogonal.
7. Um operador linear T do plano é ortogonal quando sua matriz relativamente a uma base
ortonormal ε do plano é ortogonal. Mostre que se T é ortogonal e se ε = {e1 , e2 } é uma
base ortonormal do plano, então {T (e1 ), T (e2 )} também é uma base ortonormal do plano.
8. Seja [a, b]t a primeira coluna de uma matriz ortogonal Q.
(a) Quanto vale a2 + b2 ?
(b) Mostre, usando 6(b), que há duas escolhas possíveis para a segunda coluna de Q e
escreva as matrizes correspondentes.
(c) Mostre que é possível distinguir entre as escolhas para a segunda coluna de Q
calculando apenas o determinante de Q.
9. Seja Q a matriz obtida no exercício 8 cujo determinante é igual a 1. Mostre que Q é a
matriz de uma rotação.
10. Seja Q a matriz obtida no exercício 8 cujo determinante é igual a −1.
(a) Calcule os autovalores de Q.
(b) Use (a) para mostrar que Q é a matriz de uma reflexão.
(c) Determine o vetor diretor do espelho de Q em função de a e b.
11. Mostramos acima que todo operador ortogonal do plano é uma rotação ou uma reflexão.

Como veremos mais adiante não é verdade que todo operador ortogonal do espaço é uma
rotação ou uma reflexão.
Preenchendo a tabela abaixo você terá vários critérios para distinguir se um dado operador
ortogonal representa uma rotação ou uma reflexão.
Tipo do operador ortogonal Determinante Autovalores Matriz simétrica?
Rotação
Reflexão
TABELA 1. Distinguindo a matriz ortogonal que descreve uma rotação da
que descreve uma reflexão
8
ESTUDOS DIRIGIDOS 2014
E STUDO DIRIGIDO 4
S ISTEMAS LINEARES
Objetivo: aplicar eliminação gaussiana na solução de sistemas lineares.
Lembrete: Sejam i > j inteiros positivos e a ∈ R:
• Cij (α) é a matriz quadrada que difere da matriz identidade apenas na posição ij,
cuja entrada é igual a α;
• Fij é a matriz obtida quando trocamos a linha i com a linha j na matriz identidade.
Chamaremos as C’s de matrizes elementares e as F ’s de flips.
1. Considere os sistemas:


x + 2y + 4z
2x + 5y + 13z

4x + 8y + 19z
=7
= 23
= 43
e


2x + 3y + z
6x + 9y + 8z

10x + 39y + 25z
=3
= 24 ,
= 51
(a) Escreva o sistema em forma matricial.
(b) Determine a matriz aumentada A do sistema.
(c) Determine a forma escada de A, indicando, em cada etapa, as matrizes elementares
e flips utilizados.
(d) Resolva o sistema triangular superior obtido.
2. Para cada um dos sistemas abaixo, determine os valores de k para os quais o sistema é
(a) determinado, (b) indeterminado e (c) impossível.




=7
x
+
y
+
z
=
7
x + y + z

e
kx + ky + (k + 1)z = 7k + 2
3x + 4y + (k + 3)z
= 32


2x + (k + 2)y + 7z = 22
2x + 5y + (4k + 1)z = k 2 + 46
ÁLGEBRA LINEAR ALGORÍTMICA
9
E STUDO DIRIGIDO 5
D ETERMINANTES E INVERSÃO DE MATRIZES
Determinantes e inversão de matrizes
Objetivo: estudar aplicações da eliminação gaussiana ao cálculo de determinantes e à
inversão de matrizes.
1. Ao longo de todo este estudo dirigido denotaremos por M uma matriz genérica m × m
e por I a matriz identidade de mesmo tamanho. Suporemos, também, que








1 2 3
2
14 3
1
2
3
2
3
4








A = 6 13 23 , B = −2 −7 2 , C = −2 −4 −4 e D = −4 −6 −6 .
7 17 37
−4 −14 5
−2 −3 −1
−4 −6 −1
Determine a matriz escada obtida a partir de A, de B, de C e de D pelo algoritmo de eliminação gaussiana, indicando, as matrizes elementares utilizadas em cada etapa do processo.
O determinante de uma matriz satisfaz as seguintes propriedades:
• o determinante de um produto de matrizes é o produto dos seus determinantes;
• o determinante de uma matriz triangular (superior ou inferior) é igual ao produto
das posições ao longo da diagonal;
• se trocarmos duas linhas (ou colunas) de uma matriz o seu determinante muda de
sinal.
2. Seja U a matriz escada obtida através da aplicação da eliminação gaussiana a uma matriz
M . Supondo que nenhum flip foi utilizado ao longo do processo de eliminação, mostre que
det(M ) = det(U ). Use este método para calcular o determinante das matrizes A, B e D.
Ao contrário das matrizes elementares, os flips têm determinante igual a −1. Por isso, não
será verdade que det(M ) = det(U ) se, além das matrizes elementares, for necessário utilizar
flips no cálculo de U .

3. Qual será o valor de det(M ), em função de det(U ), se forem executados r flips no processo de eliminação gaussiana usado para achar U ? Use isto para calcular o determinante
da matriz C.
10
ESTUDOS DIRIGIDOS 2014
4. Suponha que, usando matrizes elementares e flips, você reduziu a matriz [M, I] (de
tamanho m × 2m) à forma [U, S], em que U é uma matriz escada.
(a) Qual a relação entre S e as matrizes elementares e flips utilizadas para achar U ?
(b) Qual é a matriz SM ?
(c) Reduza [A, I], [B, I], [C, I] e [D, I] à forma escada por eliminação gaussiana.
Dados inteiros i 6= j e um número real α, a matriz elementar Cij ((α)) é a matriz quadrada que difere da identidade apenas na posição ij, que está preenchida com α.
5. Até aqui as matrizes elementares que utilizamos foram todas triangulares inferiores;
isto é, foram da forma Cij (α) com i > j. Contudo, para inverter matrizes, precisaremos
também das que são triangulares superiores. Suponha, então, que i < j e que U é uma
matriz triangular superior sem nenhum posição nula na diagonal.
(a) Qual o efeito de multiplicar uma matriz M , à esquerda, for Cij (α)?
(b) Explique como achar uma matriz T , que é um produto de matrizes elementares, tal
que T U = I.
6. Dada uma matriz M , considere o seguinte algoritmo:
Etapa 1: reduza [M, I] à forma escada [U, L] usando matrizes elementares e flips;
Etapa 2: multiplique [U, L] à esquerda por D−1 em que D = diag(diag(U ));
Etapa 2: reduza [D−1 U, D−1 L] à forma [I, S] usando matrizes elementares;
Saída: retorne S.
Note que as matrizes elementares na Etapa 1 são todas triangulares inferiores e as da
Etapa 3 são todas triangulares superiores. Explique:
• porque não é necessário usar flips na Etapa 3;
• como inverter D na Etapa 2 quando não há zeros na diagonal;
• o que fazer quando há zeros na diagonal de D.
Explique porque o algoritmo acima retorna a inverse de M quando det(M ) 6= 0 e use-o
para calcular as inversas das matrizes A, B e C.
ÁLGEBRA LINEAR ALGORÍTMICA
11
E STUDO DIRIGIDO 6
P ROJEÇÕES EM n DIMENSÕES
Objetivo: estudar os operadores lineares que definem projeções do Rn .
1. Seja π o hiperplano do R3 cuja equação cartesiana é x + y + z = 0.
Determine dois vetores não colineares v1 e v2 em π.
Determine um número real α tal que v1 e w = v2 − αv1 são ortogonais entre si.
Determine as normalizações u1 e u2 de v1 e w e mostre que hv1 , v2 i = hu1 , u2 i.
Usando u1 e u2 , calcule a matriz P da projeção ortogonal do R3 sobre π.
Mostre que se v ∈ R3 e w = P v, então as coordenadas de w, relativamente ao
sistema definido pelos vetores u1 e u2 , são ut1 v e ut2 v.
(f) Determine as coordenadas de cada vértice da projeção do cubo definido por
(a)
(b)
(c)
(d)
(e)
[0, 0, 0]t , [1, 0, 0]t , [0, 1, 0]t , [0, 0, 1]t , [1, 1, 0]t , [1, 0, 1]t , [0, 1, 1]t , [1, 1, 1]t ,
no plano π usando o sistema de coordenadas determinado pelos vetores unitários
u1 e u2 e desenhe a projeção do cubo relativamente a este sistema.
2. Seja u um vetor unitário do Rn e seja r a reta gerada por u. Considere a matriz P = uut
que define a projeção do Rn sobre r.
(a) Mostre que P é simétrica e calcule P 2 .
(b) Determine o conjunto dos vetores v ∈ Rn que satisfazem P v = 0.
3. Seja u um vetor unitário do Rn e seja H o hiperplano normal a u. Considere a matriz
P = I − uut que define a projeção do Rn sobre H.
(a) Mostre que P é simétrica e calcule P 2 .
(b) Determine o conjunto dos vetores v ∈ Rn que satisfazem P v = 0.
4. Seja T um operador linear do Rn cuja matriz é simétrica e satisfaz T 2 = T . Prove que,
se apenas os múltiplos escalares de um vetor unitário u são levados no zero por T , então T
define a projeção sobre o hiperplano normal a u.
12
ESTUDOS DIRIGIDOS 2014
E STUDO DIRIGIDO 7
S UBESPAÇOS E GERADORES
Objetivo: familiarização com os conceitos de subespaços e geradores.
1. Considere os seguintes subconjuntos do R4 . Se o subconjunto for um subespaço, determine seus geradores; caso contrário, indique qual (ou quais) das propriedades de subespaço
falha para aquele conjunto.
(a)
(b)
(c)
(d)
(e)
(f)
{[x, y, z, w]t | x − y + z − w = 0};
{[x, y, z, w]t | x − y + z − w = 2};
{[x, y, z, w]t | x − y + w = x − z − 5w = 3x − 2y − z − 3w = 0};
{[x, y, z, w]t | y − x2 = 0};
{[x, y, z, w]t | x2 + y 2 = 0};
união de dois hiperplanos.
2. Considere os seguintes subconjuntos do conjunto das matrizes 3 × 3. Se o subconjunto
for um subespaço, determine seus geradores; caso contrário, indique qual (ou quais) das
propriedades de subespaço falha para aquele conjunto.
(a) o conjunto das matrizes simétricas;
(b) o conjunto das matrizes ortogonais;
(c) o conjunto das matrizes A que satisfazem AB = BA em que


1 0 1


B = 0 1 3 ;
0 0 1
(d) o conjunto das matrizes A que satisfazem A2 = 0.
ÁLGEBRA LINEAR ALGORÍTMICA
13
E STUDO DIRIGIDO 8
D EPENDÊNCIA E INDEPENDÊNCIA LINEAR
Objetivo: familiarização com os conceitos de dependência e independência linear de vetores.
1. Seja V um espaço vetorial e S = {v1 , v2 , v3 , v4 , v5 } um conjunto de vetores linearmente
independentes contidos em V . Quais dos conjuntos abaixo são linearmente dependentes, e
quais são independentes?
(a)
(b)
(c)
(d)
(e)
(f)
S1 = {v1 , v3 , v4 };
S2 = {v1 + av3 , v2 , v3 , v4 , v5 };
S3 = {v1 − v3 , v2 − v3 , v4 − v3 , v5 − v3 };
S4 = {v1 − v3 , v2 , v3 , v4 − v5 , v5 − v4 + v3 − v2 };
S5 = {v1 − a2 v2 − a3 v3 − a4 v4 − a5 v5 , v2 , v3 , v4 , v5 };
S6 = {v1 + a2 v2 + a3 v3 + a4 v4 + a5 v5 , v2 + b3 v3 + b4 v4 + b5 v5 , v3 + c4 v4 + cv5 , v4 +
d5 v5 , v5 };
em que os a’s, b’s, c’s e d’s são números reais.
2. Sejam m ≤ n números inteiros positivos e A uma matriz triangular superior de tamanho m × n que não tem posições nulas ao longo da diagonal.Mostre que as linhas de A,
consideradas como vetores em Rn , são necessariamente linearmente independentes.
3. Ache bases para os seguintes subespaços do R5 :
(a) {[x, y, z, w, u]t | x − y + z − w + u = 0};
(b) {[x, y, z, w, u]t | x − y + z − w = u − y};
(c) {[x, y, z, w, u]t | x − y + w = x − z − 5w = 3x − 2y − z − 3w = 0}.
14
ESTUDOS DIRIGIDOS 2014
E STUDO DIRIGIDO 9
I NTERSEÇÕES DE SUBESPAÇOS VETORIAIS
1. Seja V um espaço vetorial e sejam U e W dois subespaços de V . Prove que
U ∩ W = {v ∈ V | v ∈ U and v ∈ W }
também é um subespaço de V .
2. Sejam A e B matrizes de tamanhos k × n e ` × n, respectivamente, e considere os
subespaços
U = {v ∈ Rn | Av = 0} e W = {v ∈ Rn | Bv = 0}.
Determine um sistema linear cujo conjunto solução é U ∩ W .
3. Sejam U e W os seguintes subespaços de R4 :
U = {(x, y, u, w, z) | x + y − w + z = x − y + 6w + z = 0};
W = {(x, y, u, w, z) | x + y − w = 0}.
Determine uma base e a dimensão de U ∩ W .
4. Determine um sistema homogêneo do qual o subespaço
W 0 = h[1, 0, 1, 0]t , [0, 1, −1, 1]t , [0, 0, 1, −1]t , [1, 1, 1, 0]t i
seja o conjunto solução.
D ICA : Se ax + by + cz + dw = 0 for uma equação do sistema, então substituindo as
coordenadas de cada um dos vetores no lugar das variáveis x, y, z e w obtemos um sistema
homogêneo em a, b, c e d. Basta resolvê-lo e você obterá os valores de a, b, c e d como
solução do sistema.

O sistema em a, b, c e d é obviamente indeterminado: por quê?
4. Calcule uma base e a dimensão da interseção do subespaço W 0 do exercício anterior
com o subespaço U 0 gerado pelos vetores [1, 1, 1, 1]t e [1, 2, 1, 0]t .
ÁLGEBRA LINEAR ALGORÍTMICA
15
E STUDO DIRIGIDO 11
S OMAS E COMPLEMENTOS ORTOGONAIS
1. Seja V um espaço vetorial e sejam U e W dois subespaços de V e considere o conjunto:
U + W = {u + w ∈ V | u ∈ U and w ∈ W }.
(a) Mostre que U + W é um subespaço de V .
(b) Mostre que se U = hu1 , . . . , um i e W = hw1 , . . . , wn i, então U +W = hu1 , . . . , um , w1 , . . . , wn i.
(c) Dê um exemplo de dois subespaços U e W do R3 com a seguinte propriedade: se
BU é uma base de U e BW uma base de W , então BU ∪ BW não é uma base de
U + W.
2. Sejam U1 e U2 os seguintes subespaços de R4 :
U1 = {(x, y, u, z) | x + y − w + z = x − y + 6w + z = x + y − z = 0};
U2 = {(x, y, u, z) | x + y − w = y − 2z = 0}.
Determine uma base e a dimensão de U1 + U2 .
3. Seja U um subespaço do Rn e considere: U ⊥ = {v ∈ Rn | hv|ui = 0 para todo u ∈
U }.
(a) Mostre que U ⊥ é um subespaço do Rn .
(b) Se U = hu1 , . . . , um i, descreva uma matriz A tal que U ⊥ é o conjunto solução do
sistema AX = 0.
(c) Mostre que U ⊥ ∩ U = {0}.
4. Considere o subespaço do R4 definido por
U3 = h[1, 0, 1, 0]t , [0, 1, −1, 1]t , [0, 0, 1, −1]t , [1, 2, 2, −1]t , [1, 1, 2, −1]t i.
(a) Calcule uma base e a dimensão de U3 .
(b) Calcule uma base e a dimensão de U3⊥ .
(c) Determine um sistema linear cujo conjunto solução é U3 .
16
ESTUDOS DIRIGIDOS 2014
E STUDO DIRIGIDO 12
E SPAÇOS VETORIAIS & C IA
1. Seja G = {[1, 0, 0, 1]t , [0, 1, 2, 0]t , [0, 1, −1, 0]t }. Escreva cada um dos vetores abaixo
como combinação linear dos vetores de G: u = [2, 1, 3, 2]t , v = [3, 5, 10, 3]t e w =
[2, 1, 3, 7]t .
2. Determine se os seguintes subespaços de R4 são iguais ou diferentes:
U1 = h[1, −1, −3]t , [3, −2, −8]t , [2, 1, −3]t i
e
U2 = h[1, 1, −1]t , [2, 3, −1]t , [3, 1, −5]t i.
3. Considere os seguintes subespaços de R4 :
U = {[x, y, z, w]t ∈ R4 | x+z = y−w = 0} e W = h[1, 3, 11, 5]t , [1, 4, 17, 7]t , [3, 10, 27, 13]t i.
Determine:
(a)
(b)
(c)
(d)
(e)
(f)
(g)
(h)
bases para U e W ;
as dimensões de U e W ;
um sistema linear cujo conjunto solução seja W ;
uma base de R4 que contenha uma base de U ;
uma base de U + W e sua dimensão;
uma base de U ∩ W e sua dimensão;
uma base do complemento ortogonal U ⊥ de U e sua dimensão;
um subespaço U 0 tal que U + U 0 = R4 .
4. Considere os seguintes subespaços de R4 :
U = {(x, y, z, w) ∈ R4 | x − y + z = x + y − z + w = 0};
W = {(x, y, z, w) ∈ R4 | y + z − w = x + ky − w = 0}.
Determine os valores reais de k para os quais: (a) dim(U ∩W ) = 1 e (b) dim(U +W ) = 3.
ÁLGEBRA LINEAR ALGORÍTMICA
17
G ABARITO DO E STUDO D IRIGIDO 12
1. Vou fazer as contas para o vetor u = [2, 1, 3, 2]t e dar a resposta para os outros. Para
saber se u é combinação linear dos vetores de G precisamos resolver o sistema obtido ao
tomarmos
[2, 1, 3, 2]t = x[1, 0, 0, 1]t + y[0, 1, 2, 0]t + z[0, 1, −1, 0]t
que nos dá o sistema
x − 2 = z + y − 1 = −z + 2y − 3 = x − 2 = 0
cuja solução é
x = 2, y = 4/3
e
z = −1/3.
Portanto, u pode ser escrito na forma
1
4
2[1, 0, 0, 1]t + [0, 1, 2, 0]t − [0, 1, −1, 0]t .
3
3
Fazendo o mesmo para os outros dois vetores, obtemos
[3, 5, 10, 3]t = 3 · [1, 0, 0, 1]t + 0 · [0, 1, 2, 0]t + 5 · [0, 1, −1, 0]t
ao passo que [2, 1, 3, 7]t não pode ser escrito como combinação linear dos vetores de G.
2. Para saber se dois espaços vetoriais U1 e U2 são iguais, temos que mostrar que todos
os geradores de U1 pertencem a U2 e vice-versa. Mas os geradores de U1 estão em U2 se
podem ser escritos como combinação linear dos geradores de U2 . A maneira mais óbvia
de fazer isto é usar a estratégia do exercício anterior. Contudo, para verificar que cada um
dos geradores de U1 é combinação linear dos geradores de U2 precisamos resolver de um
sistema linear para cada gerador de U1 e, para verificar a inclusão U2 ⊆ U1 precisamos
resolver um sistema linear para cada vetor em U1 . Portanto, no caso do exercício precisaríamos resolver 6 sistema lineares em três variáveis. Por sorte, há uma maneira mais rápida
de fazer isto usando eliminação gaussiana. Para entender porque, digamos que queremos
saber se v ∈ Rn é combinação linear dos vetores G = {u1 , . . . , um } ⊂ Rn . Para isto
montamos a matrix (m + 1) × n cujas primeiras m linhas são os elementos de G e cuja
última última linha é v. Em seguida aplicamos eliminação gaussiana a A buscando obter
uma matriz em forma escada, mas sem nunca aplicar flips à última linha. Se a última linha
de forma escada de A só contiver zeros, então v é linearmente dependente dos vetores de
G.
Você deveria ser capaz explicar porque este método funciona, baseando-se nos resultados
provados em sala, e também encontrados nas notas de aula, relativos à eliminação gaussiana
e à dependência linear de vetores.

18
ESTUDOS DIRIGIDOS 2014
À primeira vista, mesmo usando este método, teríamos que aplicar eliminação gaussiana
a seis matrizes diferentes: uma para cada gerador de U1 relativamente aos geradores de U2
e vice-versa. Contudo, podemos executar a eliminação à matriz B de tamanho 6 × 3 cujas
3 primeiras linhas são os geradores de U1 e as três seguintes são os geradores de U2 e sem
nunca aplicar flips às últimas três linhas. Se as últimas três linhas da matriz escada de B
são nulas então cada gerador de U2 é combinação linear dos geradores de U1 e podemos
concluir que U2 ⊆ U1 . Em seguida, trocamos de posição os geradores de U1 com U2 para
determinar se U1 ⊆ U2 . No caso deste exercício, descobrimos que a forma escada de

1 −1 −3


3 −2 −8


2 1 −3


1 1 −1 é igual a




2 3 −1
3 1 −5



1 −1 −3


1
0 1


0 0
0



0 0
0




0 0
0
0 0
0
de modo que, não só os geradores de U2 são combinações lineares dos de U1 , mas o vetor
[2, 1, −3]t é combinação linear dos outros dois geradores de U1 , já que a eliminação foi
feita em dois passos sem nunca efetuar um flip. Aplicando, agora eliminação, sem nunca
usar flips que movam as últimas três linhas, à matriz


1 1 −1


2 3 −1


3 1 −5


1 −1 −3 é igual a




3 −2 −8
2 1 −3

1

0

0

0


0
0

1 −1

1 1

0 0

0 0


0 0
0 0
o que nos permite concluir que U1 ⊆ U2 . Combinando as duas inclusões, obtemos U1 =
U2 .
3. Resolvendo o sistema x + z = y − w = 0 verificamos que x = −z e y = w, de modo
que se [x, y, z, w]t ∈ U , então
[x, y, z, w]t = [−z, w, z, w]t = z[−1, 0, 1, 0]t + w[0, 1, 0, 1]t .
Logo,
BU = {[−1, 0, 1, 0], [0, 1, 0, 1]}
ÁLGEBRA LINEAR ALGORÍTMICA
é uma base de U e
gaussiana à matriz

1 3

1 4
3 10
19
dim(U ) = 2. Passando ao outro subespaço, aplicamos eliminação



11 5
1 3 11
5



17 7  obtendo a forma escada 0 1 6
2 .
27 13
0 0 −12 −4
Portanto, não há vetores redundantes no conjunto de geradores dados para U2 . Temos,
assim, que tanto
{[1, 3, 11, 5]t , [1, 4, 17, 7]t , [3, 10, 27, 13]t } quanto {[1, 3, 11, 5]t , [0, 1, 6, 2]t , [0, 0, −12, −4]t }
e dim(W ) = 3. Para achar um sistema linear cujo conjunto solução é W , devemos construir as equações em a, b, c, d obtidas a partir de ax+by+cz+dw = 0, quando substituímos
em x, y, zw as coordenadas dos vetores [1, 3, 11, 5]t , [0, 1, 6, 2]t , [0, 0, −12, −4]t . As equações são
a + 3b + 11c + 5d = b + 6c + 2d = −12c − 4d = 0.
Note que escolhemos a base em “forma escada” de W para obter o sistema porque ela
já provê um sistema triangular superior que podemos resolver por substituição reversa,
obtendo
d = −3c, b = 0 e a = 4c.
Logo, as equações lineares satisfeitas pelos vetores de W são todas da forma 4cx + cz −
3cw = 0; isto é, são todas múltiplos de 4x + z − 3w = 0. Podemos, portanto, escrever
W = {[x, y, z, w]t ∈ R4 | 4x + z − 3w = 0}
Para obter uma base do R4 que contenha uma base de U , basta completar BU com dois
vetores, de modo que o conjunto de quatro vetores resultantes seja linearmente independente. Como [−1, 0, 1, 0]t e [0, 1, 0, 1]t estão em forma escada, adicionamos vetores de
modo a produzir uma matriz 4 × 4 em forma triangular superior e sem zeros na diagonal.
Por exemplo,
{[−1, 0, 1, 0]t , [0, 1, 0, 1]t , [0, 0, 1, 0]t , [0, 0, 0, 1]t }
é uma base que satisfaz a propriedade desejada. Sabemos do Estudo Dirigido anterior que,
juntando geradores de U com geradores de W obtemos geradores para U + W . No caso
deste exercício, temos que
U + W = h[−1, 0, 1, 0]t , [0, 1, 0, 1]t , [1, 3, 11, 5]t , [0, 1, 6, 2]t , [0, 0, −12, −4]t i
O conjunto de geradores para U + W obtido juntando-se geradores com geradores de W não
é necessariamente uma base de U + W , mesmo quando os geradores que escolhemos para
U e W são bases de U e de W , respectivamente. No caso deste exemplo os vetores têm que ser
linearmente dependentes porque a quantidade máxima de vetores linearmente independentes em
um dado espaço vetorial é a sua dimensão, que neste caso é 4.

20
ESTUDOS DIRIGIDOS 2014
Aplicando, então, eliminação gaussiana à matriz


−1 0 1
0


0 1 0
1



 1 3 11
5




2
0 1 6
0 0 −12 −4
cujas linhas são os geradores de U + W , descobrimos que apenas uma linha se anula, de
forma que existem 4 vetores linearmente independentes em U + W . Em outras palavras,
U + W tem dimensão 4 e coincide com o R4 . Para obter U ∩ W precisamos resolver o
sistema obtido reunindo as equações que definem U com aquelas que definem W , que em
nosso caso corresponderia ao sistema linear
x + z = y − w = 4x + z − 3w = 0
cuja matriz é


1 0 1 0


0 1 0 −1 .
4 0 1 −3
Aplicando eliminação gaussiana a esta matriz, obtemos


1 0 1
0


0 1 0 −1 ,
0 0 −3 −3
que corresponde ao sistema triangular
x + z = y − w = −z − w = 0.
Resolvendo este sistema por substituição reversa, temos que z = −w, y = w e x = w;
donde
[x, y, z, w]t = [w, w, −w, w]t = w[1, 1, −1, 1]t .
Portanto, uma base para U ∩ W é {[1, 1, −1, 1]t } e dim(U ∩ W ) = 1. Observe que não
precisaríamos de calcular uma base para U ∩ W para descobrir sua dimensão, porque,
como vimos anteriormente,
dim(U + W ) = dim(U ) + dim(W ) − dim(U ∩ W ),
de modo que
dim(U ∩ W ) = dim(U ) + dim(W ) − dim(U + W ) = 2 + 3 − 4 = 1.
Passando ao complemento ortogonal de U , sabemos que U é definido como o conjunto
solução do sistema linear x + z = y − w = 0, que podemos escrever na forma
h[1, 0, 1, 0]t |[x, y, z, w]t i = h[0, 1, 0, −1]t |[x, y, z, w]t i = 0.
ÁLGEBRA LINEAR ALGORÍTMICA
21
Portanto,
U ⊥ = h[1, 0, 1, 0]t , [0, 1, 0, −1]t i.
Como estes vetores são claramente independentes, eles formam uma base de U ⊥ . Logo,
dim(U ⊥ ) = 2. Como
dim(U ) = dim(U ⊥ ) = 2,
e U ∩ U ⊥ = 0, a união de uma base de U com uma base de U ⊥ é uma base de U + U ⊥ .
Logo, dim(U + U ⊥ ) = 4. Mas, um subespaço de dimensão 4 em R4 tem que coincidir
com todo o R4 , o que nos dá U + U ⊥ = R4 . Portanto, podemos tomar U 0 = U ⊥ .
4. O subespaço U ∩ W é igual ao conjunto solução do sistema linear
x − y + z = x + y − z + w = y + z − w = x + ky − w = 0,
que equivale ao sistema trinagular
4z − 3w = 4y − w = 2x + w = (k − 6)w = 0.
Logo, se k 6= 6, então resta
4z = 4y = 2x = w = 0,
de modo que, se k 6= 0, então U ∩ W = {0}. Por outro lado, se k = 6, então
1
1
3
z = w, y = w, e x = w.4z − 3w = 4y − w = 2x + w =
4
4
2
t
e teremos que [x, y, z, w] ∈ U ∩ W se, e somente se,
1
[x, y, z, w]t = w[−2, 1, 3, 4]t
4
Portanto, dim(U ∩ W ) = 1 quando k = 6. Para descobrir o que acontece com U + W no
caso em que k = 6, precisamos conhecer as dimensões de U e W . Aplicando eliminação,
reduzimos o sistema que define U à forma triangular, obtendo
x − y + z = 2y − 2z + w = 0.
Como os elementos de U dependem de dois parâmetros livres, temos que dim(U ) = 2.
No caso de W , o sistema já está em forma triangular e tem duas equações, de modo que
dim(W ) = 2. Como já vimos que dim(U ∩ W ) = 0 quando k = 6, obtemos
dim(U + W ) = dim(U ) + dim(W ) − dim(U ∩ W ) = 2 + 2 − 1 = 3.
Como já vimos que dim(U ∩ W ) = 0 quando k 6= 6, obtemos
dim(U + W ) = dim(U ) + dim(W ) − dim(U ∩ W ) = 2 + 2 − 0 = 4.
Resumindo, quando
k 6= 6: dim(U ∩ W ) = 0 e dim(U + W ) = 4;
k = 6: dim(U ∩ W ) = 1 e dim(U + W ) = 3.
22
ESTUDOS DIRIGIDOS 2014
E STUDO DIRIGIDO 13
T RANSFORMAÇÕES LINEARES E MATRIZES
Objetivo: definir transformação linear e mostrar que, uma vez fixadas bases nos espaços
de partida e chegada, é possível descrever uma transforma linear através de uma matriz.
Definição. Seja V um espaço vetorial do qual B = {v1 , . . . , vn } é uma base. Por definição,
qualquer vetor v ∈ V pode ser escrito como combinação linear dos vetores de B. Se
v = α1 v1 + · · · + αn vn em que α1 , . . . , αn ∈ R,
então dizemos que α1 , . . . , αn são as coordenadas de v relativamente à base B e escrevemos (v)B = [α1 , . . . , αn ]t .
Note que a ordem em que os vetores aparecem listados em uma base é essencial na determinação das coordenadas de um vetor relativamente àquela base. Infelizmente o uso consagrou
o uso de chaves para escrever uma base, como se elas fossem conjuntos (em que a ordem não
importa); quando, na verdade, são listas de vetores.

Exercício 1: Calcule as coordenadas dos vetores [1, 2, 3, 4]t e [4, 0, 1, 7]t , relativamente à
base B = {[1, 1, 1, 1]t , [0, 1, 1, 1]t , [0, 0, 1, 1]t , [0, 0, 0, 1]t }.
Exercício 2: Seja B = {u1 , . . . , un } uma base ortonormal do Rn . Mostre que se v ∈ Rn ,
então (v)B = [hv | u1 i, . . . , hv | un i]t
Exercício 3: Calcule as coordenadas dos vetores [1, 2, 3, 4]t e [4, 0, 1, 7]t , relativamente à
base
1
1
1
1
t
t
t
t
β = √ [1, 0, 1, 0] , √ [0, 1, 0, 1] , √ [−1, 0, 1, 0] , √ [0, 1, 0, −1] .
2
2
2
2
Definição. Sejam V e W espaços vetoriais. Uma transformação linear de V em W é uma
aplicação T : V → W que satisfaz
T (v + v 0 ) = T (v) + T (v 0 )
e
T (λv) = λT (v),
quaisquer que sejam os vetores v, v 0 ∈ V e o escalar λ ∈ R. Quando V = W dizemos que
a transformação é um operador linear.
Exercício 4: Suponha que:
• V é um espaço vetorial cuja base é β = {v1 , v2 , v3 };
ÁLGEBRA LINEAR ALGORÍTMICA
•
•
•
•
23
W é um espaço vetorial cuja base é γ = {w1 , w2 , w3 , w4 };
T : V → W é uma transformação linear;
v ∈ V tem coordenadas (v)β = [α1 , α2 , α3 ]t ;
(T (vj ))γ = [aj , bj , cj , dj ]t para j = 1, 2 e 3.
(a) Use as propriedades que definem uma transformação linear para calcular (T (v))γ
em função das coordenadas de V relativamente à base β e das coordenadas de
T (v1 ), T (v2 ) e T (v3 ) relativamente à base γ.
(b) Determine uma matriz A de tamanho 4 × 3 tal que (T v)γ = A · (v)β .
Definição Suponha que T : V → W é uma transformação linear entre dois espaços vetorias V e W e que β é uma base de V e γ é uma base de W . A matriz da transformação T
relativamente às bases β e γ é


|
|
···
|


(T )βγ = T (v1 )γ T (v2 )γ · · · T (vn )γ  ,
|
|
···
|
cujas colunas são formadas pelas coordenadas de T (v1 )γ , . . . , T (vn )γ . Esta matriz satisfaz
a equação (T v)γ = (T )βγ (v)β .
Exercício 5: Calcule a matriz (T )αβ da transformação linear T : R3 → R4 definida por
T (x, y, z) = [x − y, x + y, x + z, z − w]t relativamente à base α do R3 cujos vetores são
[1, 1, 1]t , [1, 2, 4]t e [1, 3, 9]t e à base β do R4 definida no Exercício 3.
Exercício 6: Calcule a matriz (S)Bε da transformação linear S : R4 → R3 definida por
T (x, y, z, w) = [x + z − w, x + y + z, x + z − w]t relativamente à base B do R4 definida
no Exercício 1 e à base canônica ε do R3 .
Exercício 7: Calcule a matriz (S)Bε da transformação linear S : R4 → R3 definida por
T (x, y, z, w) = [x + z − w, x + y + z, x + z − w]t relativamente à base B do R4 definida
no Exercício 1 e à base canônica ε do R3 .
Exercício 8: Calcule a matriz (S)εγ da transformação linear S : R4 → R3 definida por
T (x, y, z, w) = [x + z√− w, x + y + z, x√+ z − w]t relativamente à base canônica do R4 e
à base γ = {[1, 0, 1]t / 2, [1, 0, −1]t / 2, [0, 1, 0]t } do R3 .
E STUDO DIRIGIDO 14
M UDANÇA DE BASE
24
ESTUDOS DIRIGIDOS 2014
Objetivo: descrever de que forma o conhecimento da matriz de uma transformação linear
em uma dada base nos permite obter a matriz do mesmo operador em uma base diferente.
Cenas do episódio anterior. No episódio anterior de Álgebra Linear Algorítmica vimos
que se T : V → W é uma transformação linear entre dois espaços vetorias, β é uma base
de V e γ uma base de W , então (T )βγ (matriz de T relativamente às bases β e γ) é a matriz
de tamanho dim(W ) × dim(V ) cujas colunas são T (v1 )γ , . . . , T (vn )γ . Esta matriz satisfaz
(T v)γ = (T )βγ (v)β
(5)
que é a equação mais importante desta parte do curso, já que quase tudo que faremos será
baseado nela.
Definição. Seja V um espaço vetorial do qual B = {v1 , . . . , vn } e B 0 = {v10 , . . . , vn0 } são
bases. Aplicando a fórmula (5) ao operador identdade id : V → V e tomando β = B e
γ = B 0 , obtemos
(v)B 0 = (id)BB 0 (v)B .
A matriz (id)BB 0 é chamada de matriz de mudança de base entre as bases B e B 0 , porque
ela converte as coordenadas de um vetor relativamente à base B nas coordenadas do mesmo
vetor na base B 0 .
Exercício 1: Descreva as colunas de (id)BB 0 em termos dos vetores de B e B 0 .
Exercício 2: Determine a matriz de mudança de base (id)βε , quando β é a base do R5
formada pelos vetores
v1 = [a1 , b1 , c1 , d1 , e1 ]t , . . . , v5 = [a5 , b5 , c5 , d5 , e5 ]t
e ε é a base canônica do R5 .
Exercício 3: Considere as bases do R4 dadas abaixo:
α = {{[1, 1, 1, 1]t , [0, 1, 1, 1]t , [0, 0, 1, 1]t , [0, 0, 0, 1]t }
1
1
1
1
t
t
t
t
β = √ [1, 0, 1, 0] , √ [0, 1, 0, 1] , √ [−1, 0, 1, 0] , √ [0, 1, 0, −1] .
2
2
2
2
Detemine as matrizes de mudança de base (id)αβ , (id)αε , e (id)εβ , em que ε é a base
canônica do R4 .
ÁLGEBRA LINEAR ALGORÍTMICA
25
Exercício 4: Seja B1 = {[1, 0, 1]t , [1, 1, 0]t , [0, 1, 1]t }. Determine B2 , sabendo-se que é
uma base de R3 e que a matriz de mudança de base


1 1 1


(id)B2 B1 = 1 2 4 .
0 3 9
Exercício 5: Seja V um espaço vetorial e sejam B e B 0 bases de V . Substituindo
(v)B 0 = (id)BB 0 (v)B
na fórmula
(v)B = (id)B 0 B (v)B 0
determine (id)B 0 B (id)BB 0 . Qual a relação entre estas duas matrizes?
L EMBRETE : se A1 e A2 são matrizes n × n tais que A1 v = A2 v para todo vetor v ∈ Rn ,
então A = B.
Exercício 6: Seja B1 = {[1, 0, 1]t , [1, 1, 0]t , [1, 1, 1]t }. Determine B2 , sabendo-se que é
uma base de R3 e que a matriz de mudança de base (id)B1 B2 é


1 1 −1


(id)B1 B2 = 0 1 1  .
0 0 1
Exercício 7: Sejam β = {v1 , . . . , vn } uma base ortonormal e ε a base canônica do Rn .
(a) Mostre que a matriz (id)βε é ortogonal.
(b) Calcule (id)εβ .
Exercício 8: Calcule (id)εβ em que β é a base definida no Exercício 3.
E STUDO DIRIGIDO 15
M UDANÇA DE BASE E ROTAÇÕES
As hipóteses: Sejam:
• T : V → W uma transformação linear entre dois espaços vetoriais V e W ;
• α e γ bases de V ;
• β e η bases de W .
26
ESTUDOS DIRIGIDOS 2014
Matriz de uma transformação linear: A matriz de T relativamente às bases α e β é a
matriz (T )αβ , de tamanho dim(W ) × dim(V ), cujas colunas são T (v1 )β , . . . , T (vn )β , em
que α = {v1 , . . . , vn }.
Fórmula chave: A matriz de T relativamente às bases α e β satisfaz:
(T v)β = (T )αβ (v)α
Mudança de base em vetores: Aplicando a fórmula chave com V = W , β = γ e T = id,
obtemos:
(v)γ = (id)αγ (v)α ,
em que (id)αγ é conhecida como a matriz de mudança de base.
Mudança de base em transformações lineares: Combinando a fórmula chave com a
mudança de base para vetores, obtemos
(T )γη = (id)βη (T )αβ (id)γα ,
que nos permite calcular a matriz de T relativamente às bases γ e η, quando conhecemos a
matriz de T relativamente às bases α e β.

Lembre-se que (id)αγ = (id)−1
γα .
Exercício 1: Mostre que se β é uma base ortonormal do Rn , então a matriz de mudança
de base (id)βε é ortogonal; isto é, (id)tβε · (id)βε = I.
Exercício 2: Dado o operador T do R4 definido por
T (x, y, z, w) = [x − y + 2z,
4x + 2y + 6z,
y + z,
3x − z]t
e a base
1
t 1
t 1
t 1
t
β = √ [1, 0, 1, 0] , √ [1, 0, −1, 0] , √ [0, 1, 0, 1] , √ [0, 1, 0, −1] ;
2
2
2
2
determine as matrizes (T )βε , (T )εβ , (T )εε e (T )ββ .
Exercício 3: Seja
β=
1
1
√ [1, 1, 0]t , √ [1, −1, 0]t , [0, 0, 1]t
2
2
uma base de R3 . Determine:
(a) as matrizes de mudança de base (id)βε e (id)εβ ;
ÁLGEBRA LINEAR ALGORÍTMICA
27
(b) a equação cartesiana, em relação às coordenadas na base β, do plano gerado pelos
vetores [1, 0, 1]t e [0, 1, 1]t .
Exercício 4: Determine matriz da rotação de ângulo π/3 e eixo [1, 1, 1]t , relativamente à
base canônica.
Exercício 5: Seja ρ uma rotação de eixo ` em R3 e v = [1, 1, 1]t um vetor ortogonal a `.
Sabendo-se que ρ(v) = [1, −1, 1]t , determine:
(a) o cosseno do ângulo de rotação de ρ;
(b) o eixo da rotação ρ;
(c) a matriz de ρ na base canônica.
Exercício 6: Seja ρ uma rotação de eixo [1, 1, 0]t em R3 . Sabendo-se que ρ([1, 1, 1]t ) =
[1, 5, −1]t /3, determine:
(a) o cosseno do ângulo de rotação de ρ;
(b) a matriz de ρ na base canônica.
O ângulo de rotação é medido sobre o plano ortogonal ao eixo. Como [1, 1, 1]t e [1, 1, 0]t não
são perpendiculares, então o ângulo entre [1, 1, 1]t e ρ([1, 1, 1]t ) não é o ângulo de rotação.
Para achar o ângulo de rotação correto, projete [1, 1, 1]t e ρ([1, 1, 1]t ) sobre o plano ortogonal ao
eixo e calcule o cosseno do ângulo entre estes vetores.

28
ESTUDOS DIRIGIDOS 2014
G ABARITO DO E STUDO D IRIGIDO 15
E STUDO DIRIGIDO 15
M UDANÇA DE BASE E ROTAÇÕES
As hipóteses: Sejam:
• T : V → W uma transformação linear entre dois espaços vetoriais V e W ;
• α e γ bases de V ;
• β e η bases de W .
Matriz de uma transformação linear: A matriz de T relativamente às bases α e β é a
matriz (T )αβ , de tamanho dim(W ) × dim(V ), cujas colunas são T (v1 )β , . . . , T (vn )β , em
que α = {v1 , . . . , vn }.
Fórmula chave: A matriz de T relativamente às bases α e β satisfaz:
(T v)β = (T )αβ (v)α
Mudança de base em vetores: Aplicando a fórmula chave com V = W , β = γ e T = id,
obtemos:
(v)γ = (id)αγ (v)α ,
em que (id)αγ é conhecida como a matriz de mudança de base.
Mudança de base em transformações lineares: Combinando a fórmula chave com a
mudança de base para vetores, obtemos
(T )γη = (id)βη (T )αβ (id)γα ,
que nos permite calcular a matriz de T relativamente às bases γ e η, quando conhecemos a
matriz de T relativamente às bases α e β.

Lembre-se que (id)αγ = (id)−1
γα .
ÁLGEBRA LINEAR ALGORÍTMICA
29
Exercício 1: Mostre que se β é uma base ortonormal do Rn , então a matriz de mudança
de base (id)βε é ortogonal; isto é, (id)tβε · (id)βε = I.
Exercício 2: Dado o operador T do R4 definido por
T (x, y, z, w) = [x − y + 2z,
4x + 2y + 6z,
y + z,
3x − z]t
e a base
1
t 1
t 1
t 1
t
β = √ [1, 0, 1, 0] , √ [1, 0, −1, 0] , √ [0, 1, 0, 1] , √ [0, 1, 0, −1] ;
2
2
2
2
determine as matrizes (T )βε , (T )εβ , (T )εε e (T )ββ .
Exercício 3: Seja
β=
1
1
√ [1, 1, 0]t , √ [1, −1, 0]t , [0, 0, 1]t
2
2
uma base de R3 . Determine:
(a) as matrizes de mudança de base (id)βε e (id)εβ ;
(b) a equação cartesiana, em relação às coordenadas na base β, do plano gerado pelos
vetores [1, 0, 1]t e [0, 1, 1]t .
Exercício 4: Determine matriz da rotação de ângulo π/3 e eixo [1, 1, 1]t , relativamente à
base canônica.
Exercício 5: Seja ρ uma rotação de eixo ` em R3 e v = [1, 1, 1]t um vetor ortogonal a `.
Sabendo-se que ρ(v) = [1, −1, 1]t , determine:
(a) o cosseno do ângulo de rotação de ρ;
(b) o eixo da rotação ρ;
(c) a matriz de ρ na base canônica.
Exercício 6: Seja ρ uma rotação de eixo [1, 1, 0]t em R3 . Sabendo-se que ρ([1, 1, 1]t ) =
[1, 5, −1]t /3, determine:
(a) o cosseno do ângulo de rotação de ρ;
(b) a matriz de ρ na base canônica.
O ângulo de rotação é medido sobre o plano ortogonal ao eixo. Como [1, 1, 1]t e [1, 1, 0]t não
são perpendiculares, então o ângulo entre [1, 1, 1]t e ρ([1, 1, 1]t ) não é o ângulo de rotação.
Para achar o ângulo de rotação correto, projete [1, 1, 1]t e ρ([1, 1, 1]t ) sobre o plano ortogonal ao
eixo e calcule o cosseno do ângulo entre estes vetores.

30
ESTUDOS DIRIGIDOS 2014
G ABARITO DO E STUDO D IRIGIDO 15
Exercício 1: Se β = {u1 , . . . un } é uma base ortonormal do Rn , então


| | ··· |


(id)βε = v1 v2 · · · vn  ,
|
|
···
|
de modo que
(id)tβε (id)βε



−− v1t −−


| | ···
−− v2 −− 
=
..
.. 
 ..
 · · v1 v2 · · ·
.
.
. 

| | ···
−− vnt −−

v1t v1 v1t v2 · · ·
 t
|
v2 v1 v2t v2 · · ·
 

vn  =  .
..
..
.
.
 ..
|
vnt v1 vnt v2 · · ·


v1t vn

v2t vn 
.. 
.
. 
vnt vn
Como a base é ortonormal, temos que
(
1
vit vj = hvi | vj i =
0
se i = j
,
se i 6= j
de modo que (id)tβε · (id)βε é a matriz identidade n × n.
Exercício 2: As matrizes

1 −1 2

4 2
6
(T )εε = 
0 1
1

3 0 −1

0

0

0

0

e
(T )βε

3 −1 −1 −1


10 −2 2
2
1 


=√ 
1
0
20 1

3 0 −1 0
podem ser calculadas facilmente a partir da definição.
mudança de base, que nos dá

1

1 1
(T )εβ = (id)εβ (T )εε = √ 
2
7
1
e também

(T )ββ = (id)εβ (T )εε (id)βε
Para as outras duas é melhor usar
0
−2
2
2
3
1
5
7

0

0

0

0

4 −2 0
0



2
0
−2
−2
1
.
= 

2 12 2
2
2

8 −6 2
2
ÁLGEBRA LINEAR ALGORÍTMICA
31
Lembre-se que, como a base β é ortonormal, então (id)εβ = (id)tβε .
Exercício 3: As matrizes de mudança de base são


1 1 0
1 

(id)βε = √ 1 −1 0 e
2
0 0 1
(id)εβ = (id)tβε .
As coordenadas na base β dos vetores v1 = [1, 0, 1]t e v2 = [0, 1, 1]t são:
h p
i
h p
i
p
p
(id)εβ (v1 )β = 1/ (2) 1/ (2) 1 (id)εβ (v2 )β = 1/ (2) −1/ (2) 1 .
Para achar a equação cartesiana precisamos de um vetor normal a estes dois. Para isto
basta resolver o sistema
h
ih p
i h
ih p
i
p
p
x y z 1/ (2) 1/ (2) 1 = x y z 1/ (2) −1/ (2) 1 = 0
√
que tem como solução os múltiplos do vetor [− 2, 0, 1]. Logo, a equação cartesiana do
plano desejado é
√
− 2x0 + z 0 = 0
em que x0 , y 0 e z 0 representam coordenadas na base β.
Exercício 4: A matriz da rotação de ângulo π/3 e eixo [1, 1, 1]t relativamente à base ortonormal
1
t 1
t 1
t
β = √ [1, 1, 1] , √ [1, −1, 0] , √ [−1, −1, 2]
3
2
6
é


1
0
0
√ 

(T )β = 0 1/2 − 3/2 .
√
3/2
1/2
0
Portanto,
(T )εε = (id)βε (T )ββ (id)εβ ,
em que
√1
3
 √1
 3
√1
3

(id)βε =
pois β é base ortonormal do R3 .
√1
2
− √12
− √16
0
√2
6


− √16 
e
(id)εβ = (id)tβε ,
32
ESTUDOS DIRIGIDOS 2014
Exercício 5: O cosseno do ângulo de rotação θ é
cos(θ) =
hv | ρ(v)i
1
= .
kvkkρ(v)k
3
Como é dito que v é ortogonal ao eixo de rotação, então o mesmo vale para ρ(v), de modo
que o eixo será ao longo da reta solução do sistema
h[x, y, z]t |[1, 1, 1]t i = h[x, y, z]t |[1, −1, 1]t i = 0;
que tem como vetor diretor [1, 0, −1]t . Para determinar a matriz (ρ)ε , precisamos primeiramente achar a√matriz desta rotação relativamente a uma base ortonormal cujos vetores
são [1, 0, −1]t / 2 e dois vetores no plano gerado por v e ρ(v). Como v e ρ(v) não são
ortogonais, aplicaremos Gram-Schimdt para ortonormalizá-los. Se
v
1
u1 =
= √ [1, 1, 1]t ,
kvk
3
então
1
w = [1, −1, 1] − [1, 1, 1]t = [2, −4, 2]t
3
de modo que
1
u2 = √ [1, −2, 1]t ,
6
é o segundo vetor de uma base ortonormal do plano perpendicular ao eixo da rotação; de
modo que podemos tomar
1
t 1
t 1
t
β = √ [1, 0, −1] , √ [1, 1, 1] , √ [1, −2, 1] .
2
3
6
Para poder escrever a matriz de T na base β ainda precisamos achar o seno do ângulo de
rotação. Como


1
0
0


(ρ)β = 0
1/3
− sen (θ) ,
0
sen (θ)
1/3
basta achar a coordenada de ρ(u1 ) relativamente à base β, porque isto nos dá o valor da
entrada na terceira linha e segunda coluna da matriz (ρ(beta)). Contudo,
v
1
u1 =
= √ [1, 1, 1]t ,
kvk
3
de modo que
ρ(v)
1
ρ(u1 ) =
= √ [1, −1, 1]t .
kvk
3
Como β é uma base ortonormal, a coordenada desejada é igual a
4
hρ(u1 ) | u2 i = √ .
3 2
ÁLGEBRA LINEAR ALGORÍTMICA
33
Assim,


1 0
0


(ρ)β = 0 1/3 − 3√4 2 
0
4
√
3 2

e
√1
2

(id)βε =  0
1/3
√1
2
√1
3
√1
3
√1
3
√1
6

− √26 
√1
6

de modo que
(ρ)εε = (id)βε (ρ)ββ (id)tβε ,
já que β é ortonormal.
Exercício 6: Como o ângulo de rotação é medido sobre o plano ortogonal ao eixo e [1, 1, 1]t
não é perpendicular a [1, 1, 0]t , então o ângulo entre [1, 1, 1]t e ρ([1, 1, 1]t ) não é o ângulo
de rotação. Para achar o ângulo de rotação correto, projetamos [1, 1, 1]t e ρ([1, 1, 1]t )
sobre o plano ortogonal ao eixo e calculamos o cosseno do ângulo entre estes dois vetores.
Começamos determinando a matriz P da projeção sobre o plano ortogonal a [1, 1, 0]t , que
é


1/2 −1/2 0


P = I − uut = −1/2 1/2 0
0
0
1
√
em que u = [1, 1, 0]t / 2. Projetando os vetores [1, 1, 1]t e ρ([1, 1, 1]t ), obtemos
1
1
t
t
[1, 5, −1] = [−2, 2, −1]t .
P [1, 1, 1] = [0, 0, 1] e P
3
3
Portanto, o cosseno do ângulo de rotação θ é
cos(θ) =

h[0, 0, 1] | [−2, 2, −1]i
−1
=
3
3
Como dois vetores quaisquer nas direções de P [1, 1, 1]t e P (ρ([1, 1, 1]t ) formam o mesmo
ângulo entre si, escolhi vetores cujas entradas facilitassem os cálculos.
Como no exercício anterior precisamos de uma base ortonormal formada por um vetor
unitário ao longo do eixo e uma base ortonormal do plano perpendicular ao eixo. Procedendo como no exercício anterior, obtemos
1
t
t 1
t
β = √ [1, 1, 0] , [0, 0, 1] , √ [1, −1, 0] .
2
2
Nesta base,


1
0
0


(ρ)β = 0 −1/3 − sen (θ) ,
0 sen (θ)
−1/3
34
ESTUDOS DIRIGIDOS 2014
de forma sen (θ) é igual à terceira coordenada de [0, 0, 1]t relativamente à base β. Como β
é uma base ortonormal, a coordenada desejada é igual a
1
−4
t
t 1
√ [1, −1, 0] | [−2, 2, −1] = √ .
3
2
3 2
Assim,


 √
√ 
1
0
0
1/ 2 0 1/ 2
√ 
√ 

 √
(ρ)β = 0 −1/3 4/3 2 , e (id)βε = 1/ 2 0 −1/ 2
√
0 −43 2 −1/3
0
1
0
de modo que
(ρ)εε = (id)βε (ρ)ββ (id)tβε ,
já que β é ortonormal.