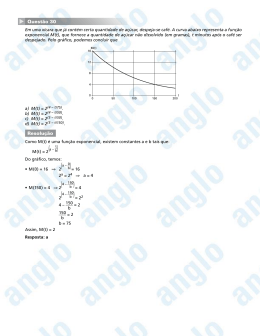
COMPOSIÇÕES DE FUNÇÕES GERATRIZES
E A FÓRMULA EXPONENCIAL
Grande parte do poder de funções geratrizes vêm de composição delas!
Observação. Sejam
F (x) =
X
fn xn
n≥0
G(x) =
X
gn xn
n≥0
duas séries formais. A composição F (G(x)) é bem definida desde que g0 = 0.
Exemplo 0.1. Dada uma função f : N → C, vamos calcular
X
g(n) =
f (a1 )f (a2 ) . . . f (ak )
onde a soma percorre todas as composições a1 + a2 + . . . + ak = n, onde
ai ≥ 1, e k ≥ 1. Por exemplo
g(3) = f (3) + f (1)f (2) + f (2)f (1) + f (1)f (1)f (1)
Seja
F (x) =
X
f (n)xn
n≥1
G(x) = 1+
X
g(n)xn
n≥1
Observe que
G(x) =
1
1 − F (x)
Use o exemplo acima para resolver os seguintes problemas.
Exercício 1. Mostre que
X
a1 a2 . . . ak = F2n
onde a soma é sobre todas as composições a1 +. . .+ak = n, e F• é a sequência
de Fibonacci.
Exercício 2. Mostre que
X
(2a1 −1 − 1) . . . (2ak −1 − 1) = F2n−2
onde a soma é sobre todas as composições a1 + . . . + ak = n.
Exercício 3. Mostre que
X
2{#i | ai =1} = F2n+1
onde a soma é sobre todas as composições a1 + . . . + ak = n.
Date: Terça Feira, 26 de Junho de 2012.
1
2
G. BUJOKAS
1. Significado combinatório
A partir dessa seção, nós vamos precisar de funções geratrizes exponenciais. Vamos usar a seguinte notação. Para uma função f : N → C, nós
associamos
X
xn
f (n)
Ef (x) =
n!
n≥0
Dada duas funções f, g, nós queremos entender qual é o significado de
Ef (Eg (x)) (essa expressão é bem definida se g(0) = 0).
Vamos usar a seguinte notação. Para um conjunto finito S, seja
#S = o número de elementos de S
P(S) = o conjunto de todos os subconjuntos não vazios de S
Π(S) = {{S1 , . . . , Sk } ⊂ P(S) | S1 ∪ S2 ∪ . . . ∪ Sk = S e Si ∩ Sj = ∅ para i 6= j}
O conjunto Π(S) vai ser chamado o conjunto de partições de S. Observe que o conjunto de partições de {1, 2, . . . , n} não é igual ao conjunto de
partições do inteiro n. Por exemplo
Π({1, 2, 3}) = {{{1, 2, 3}}, {{1, 2}, {3}}, {{1}, {2, 3}}, {{1, 3}, {2}}, {{1}, {2}, {3}}}
Teorema 1.1. Dadas funções f, g, defina uma função h satisfazendo
X
h(#S) =
g(k)f (#S1 )f (#S2 ) . . . f (#Sk )
{S1 ,...,Sk }∈Π(S)
para qualquer conjunto finito S. Então
Eh (x) = Eg (Ef (x))
Exemplo 1.1. Suponha que f (#S) é o números de maneiras de dar uma
“estrutura F” nos elementos de S, e g(#S) para uma “estrutura G”. Então
h(#S) é o número de maneiras de dividir os elementos de S em grupos, e
aplicar uma estrutura F em cada grupo, e uma estrutura G no conjunto de
grupos.
Figura 1. “Filas organizadas em círculo”
A FÓRMULA EXPONENCIAL
3
Por exemplo, considere o seguinte problema. Nós queremos dividir um
conjunto de n pessoas em grupos, colocar cada grupo em um fila, e organizar
os as filas em um círculo (como na figura 1). Qual é o número an de maneiras
de fazer isso?
Seja f (n) = n! o número de maneiras de colocar n pessoas em uma fila, e
g(n) = (n − 1)! o número de maneiras de colocar n elementos em um círculo.
Então
X xn X
x
=
Ef (x) =
xn =
n!
n!
1−x
n≥1
n≥1
Eg (x) = 1 +
X
(n − 1)!
n≥1
X xn
xn
=1+
= 1 − log(1 − x)
n!
n
n≥1
Pelo teorema 1.1,
Ea (x) = Eg (Ef (x))
= 1 − log 1 −
x
1−x
= 1 − log(1 − 2x) − (− log(1 − x))
X
xn
=1+
(2n − 1)
n
n≥1
=1+
X
(2n − 1)(n − 1)!
n≥1
xn
n!
Portanto, an = (2n − 1)(n − 1)!.
Exercício 4. Prove que an = (2n − 1)(n − 1)! usando uma bijeção.
Exercício 5. Algumas crianças brincam assim: elas se dividem em grupos,
e em cada grupo uma criança fica no centro, e as outras crianças do grupo
formam uma roda em volta dela. A roda pode ter apenas uma criança (nesse
caso, ela segura suas próprias mãos), mas sempre tem que ter uma criança no
centro. Seja c(n) o número de configurações que n crianças podem formar.
Calcule a função geratriz exponencial de c(n).
Calcule também a função geratriz exponencial
XX
xn
ck (n)tk
n!
n≥0 k≥0
onde ck (n) é o número de configurações com exatamente k rodas.
2. A fórmula exponencial
As aplicações mais comuns de mais comum do teorema 1.1 são com g(n) =
1, isso é, com
X xn
Eg (x) = exp(x) =
n!
n≥0
É tão comum que merece ser enunciado como um corolário:
4
G. BUJOKAS
Corolário 2.1 (Fórmula exponencial). Dada uma função f , defina uma
função g satisfazendo
X
f (#S1 )f (#S2 ) . . . f (#Sk )
g(#S) =
{S1 ,...,Sk }∈Π(S)
para qualquer conjunto finito S. Então
Eg (x) = exp(Ef (x))
Exemplo 2.1. A intuição é que várias estruturas são formadas por componenn
tes conexas. Por exemplo, o número g(n)(= 2( 2 ) ) de grafos com n vértices, e
o número f (n) de grafos conexos. Ou o número g(n) de florestas, e o número
f (n) de árvores. Usando a fórmula exponencial, a gente consegue construir
uma sequência da outra.
Por exemplo, uma permutação w é uma união disjunta de ciclos. Seja
c(n) = (n − 1)! o número de maneiras de colocar n objetos em um ciclo.
Então
X
xn X xn
Ec (x) =
(n − 1)!
=
= − log(1 − x)
n!
n
n≥1
n≥1
Se b(n) = n! é o número de permutações, então
Eb (x) = exp(Ec (x)) = exp(− log(1 − x)) =
X xn
1
=
n!
1−x
n!
n≥0
o que é coerente.
Exercício 6. Seja an o número de permutações de n elementos em que todos
os ciclos tem tamanho 2 ou 1 (isso é, w é uma involução).
(a) Calcule a função geratriz exponencial de an .
(b) Seja In ⊂ Sn o subconjunto de involuções (então an = #In ), e Fix(w) o
número de pontos fixos de w ∈ Sn . Calcule
X X
xn
tFix(w)
n!
n≥0 w∈In
(c) Conclua que para qualquer n ≥ k,
X Fix(w)
w∈In
k
n
=
an−k
k
(d) Prove essa identidade usando uma bijeção.
Exemplo 2.2. A gente pode usar a idéia acima para construir a seguinte
função geratriz. Dada uma permutação w de n elementos, seja
ck (w) = o número de ciclos de tamanho k
e defina
c (w) c (w)
C(w) = t11 t22 . . . tncn (w)
o monomial indicador de ciclos. Seja Sn o conjunto de todas as permutações
de um conjunto de n elementos. Vamos compactar toda a informação dos
monômios indicadores na seguinte função geratriz:
X X
xn
F (x, t1 , t2 , . . .) =
C(w)
n!
n≥0 w∈Sn
A FÓRMULA EXPONENCIAL
5
A fórmula exponencial nós dá a seguinte identidade:
x
x2
x3
+ t2 + t3 + . . .)
1
2
3
Exercício 7. Seja a(n) o número de permutações w ∈ Sn que admitem uma
raiz quadrada, isto é, existe u ∈ Sn tal que u2 = w. Mostre que
F (x, t1 , t2 , . . .) = exp(t1
a(2n + 1) = (2n + 1)a(2n)
Exercício 8. Seja f (n) o número de maneiras de escolher um subconjunto
S ⊂ {1, . . . , n} e uma permutação w ∈ Sn tal que
w(i) 6∈ S se i ∈ S
Mostre que f (n) = Fn+1 n!.
Exercício 9. Seja k ≥ 2. Mostre que o número de permutações w ∈ Sn tal
que todos os ciclos têm tamanho múltiplo de k é
12 ×2×3×. . .×(k−1)×(k+1)2 ×. . .×(2k−1)×(2k+1)2 ×(2k+2) . . .×(n−1)
Exercício 10. Prove que o número de pares (u, v) ∈ Sn tal que u2 = v 2 é
igual a p(n)n!, onde p(n) é o número de partições de n.
Exercício 11. Agora faça os exercícios 7, 8, 9 e 10 com bijeções!
3. Referências
A melhor referência que eu conheço é o excelente Enumerative Combinatorics do Richard Stanley. Esse material está no volume 2.
E-mail address: [email protected]