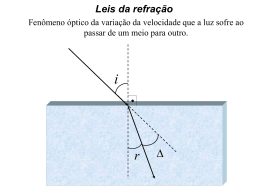
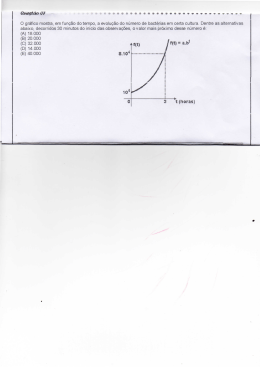
Física
QUESTÃO 04
Na figura a seguir, está esquematizado um aparato experimental que é utilizado para estudar o aumento do
número de bactérias numa solução líquida (meio de cultura), através de medidas de ângulos de refração. Um
feixe de luz monocromático I, produzido por um laser, incide do ar para a solução, fazendo um ângulo θi com a
normal à superfície líquida.
Na figura a seguir, está esquematizado um aparato experimental que é utilizado para
estudar o aumento do número de bactérias numa solução líquida (meio de cultura),
através de medidas de ângulos de refração. Um feixe de luz monocromático I,
produzido por um laser, incide do ar para a solução, fazendo um ângulo Ti com a
normal à superfície líquida.
A densidade absoluta inicial da solução, quando as bactérias são colocadas nela, é 1,05 g/cm³. Para esse valor
da densidade absoluta, o ângulo de refração medido é θr = 45°. O índice de refração da solução, Ns, varia em
função da densidade absoluta ρ de acordo com a expressão Ns = C (ρ)1/2.
a) Com base na expressão para ns acima, encontre uma unidade para a constante C.
A densidade absoluta inicial da solução, quando as bactérias são colocadas nela, é
b) À medida
em que
o tempo
passa, oabsoluta,
número de
bactérias
assim como
1,05 g/cm³.
Para esse
valor
da densidade
o ângulo
de aumenta,
refração medido
é Tr a densidade da solução. Num
certo
instante,
mede-se
o
ângulo
de
refração
em
relação
à
normal
e
encontra-se
o valor 30°, para o mesmo
= 45°. O índice de refração da solução, Ns, varia em função da densidade absoluta U
1/2
ângulo
de
incidência
do
feixe.
Calcule
a
densidade
absoluta
da
solução
neste
instante.
de acordo com a expressão Ns = C (U) .
a) Resolução:
Com base na expressão para Ns acima, encontre uma unidade para a
constante C.
a)
b)
À medida em que o tempo passa, o número de bactérias aumenta, assim
M=Massa
b) À
medida em que o tempo passa, o número de bactérias aumenta, ass
como a densidade da solução. Num certo instante, mede-se o ângulo de
L=Comprimento
a densidade da solução. Num certo instante, mede-se o ângulo de refra
refração em relação à normal e encontra-se o valor 30°, para o mesmo ânrelação
à normal e encontra-se o valor 30°, para o mesmo ângulo de in
gulo de incidência do feixe. Calcule a densidade absoluta da solução neste
do
feixe.
>N @
-1
instante. Calcule a densidade absoluta da solução neste instante.
>c@ = s12 = > Ns @>ȡ@ 2
>ȡ @
1)
> Ns @ =1
>ȡ@ =M.L-3
>c@ =1. ª¬ M.L-3 º¼
>c@ =M
-1
2
1
c ȡ
Sen i Nr
Sen i
Sen i c. 1.05
c
=
o
=
o
=
o Sen i= . 2.1
Sen r Ni
Sen 450
1
1
2
22
2
3
.L 2
2)
Sistema Internacional S.I M o Kg
>c@ =Kg
>c@ =
-1
Lom
2
.m
3
2
c
2,1 c ȡ
Sen i Nr
2
=
=
o
o ȡ=2,1g cm3
o
Sen r Ni
Sen 30
1
m3
Kg
7