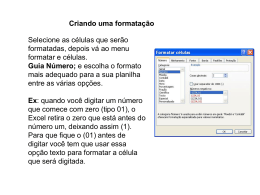
INF01040
Introdução à Programação
•
•
O computador como ferramenta de trabalho do
engenheiro
Planilha Eletrônica
Profa. Patrícia A. Jaques
Adaptado – Prof. Valter Roesler
Lâminas cedidas pela Profa. Maria Aparecida M. Souto
Sumário
• O computador como
ferramenta de
trabalho do
engenheiro
– Planilha eletrônica
– MatLab
– Linguagens de
programação
• Planilha eletrônica
– Conceito
– Elementos básicos
– Tipos de dados que
podem ser inseridos
– Selecionando células
– Formatando células
• Numéricas
• Texto
– Trabalhando com
fórmulas
• Referência relativa
• Referência absoluta
– Atividade dirigida
2
3
Elementos Básicos de uma
Planilha
• Linha: 1-16384
• Coluna: A-Z, AA ... IK  256 colunas
• Célula:
– Intersecção de uma coluna c/ uma linha
– É referenciada pela letra da coluna seguida
pelo número da linha
– Exemplo: C4
• Faixa ou Intervalo:
– Bloco de uma ou mais células que formam uma
área retangular
4
Faixas:
(A4:E4)
(B6:E14)
(A17:A21)
5
Tipos de Dados que Podem
ser Inseridos na Planilha
• Números
• Texto
• Fórmulas
– Expressão matemática
– Fica oculta sob a célula
– Na célula em si aparece o resultado da
fórmula
– Exemplo: =(A1+B1)/2
6
Prática
• Digitar planilha exemplo. Inserir bordas diferenciadas,
cores (fundo e frente), título
7
Selecionando Células
•
•
•
•
•
Uma célula
Uma faixa
Faixas não-adjacentes
Linha
Coluna
8
Faixas:
(A4:E4)
(B6:E14)
(A17:A21)
9
Formatando Células
• Fonte (A, B, C, D, ...)
•
•
•
•
Tamanho do fonte (A, B, C, D, ...)
Cor do fonte (A, B, C, D, ...)
Efeitos (negrito, itálico, sublinhado, etc.)
Inserção de
– Bordas
– Padrões
• Como?
– Menu Formatar  Células
10
Formatando Células de Texto
Total em Estoque
Total em
Estoque
11
Formatando Células Numéricas
5.690,00
R$
34.140,00
12
Formatando Células Numéricas
11-mai-04
9:10:35
13
Alargando colunas
14
Mesclando células
15
Copiar, Colar, Cortar
recortar
copiar
colar
16
Trabalhando com Fórmulas
• Uma fórmula consiste de uma combinação
de:
– Valores constantes (numérico ou texto)
– Referências à células (A1) ou função (Soma(),
Media(), Máximo(), etc.)
– Operadores aritméticos (+, -, *, /)
– Operadores de comparação (=, <>, >, <, >=, <=)
– Operador de concatenação (&)
• DEVE SER PRECEDIDA PELO SINAL DE
IGUAL “=“
17
Trabalhando com Fórmulas
• Exemplos:
=18+20
=F27/12*30
=Soma(A1:A10)
=Se(B5>=6,0; “Aprovado”;”Reprovado”)
18
Trabalhando com Fórmulas
• Qual a melhor forma para definir uma fórmula?
• Por quê?
• Porque permite RECÁLCULO rapidamente
19
Prática
• Criar fórmulas para calcular as
colunas:
– Valor em US$
– Quantidade em Estoque
• Formatar coluna Total em Estoque
para Moeda.
20
Trabalhando com Fórmulas
• Replicação de uma fórmula
– É possível copiar uma fórmula para uma
faixa de células
– Neste caso, o programa ajusta as
fórmulas de modo que funcionem
perfeitamente na nova localização
21
Replicando Fórmulas
Barra de fórmula
Ao copiar a fórmula
da célula D6 para o
intervalo D7...D14, a
referência à célula
D6 automaticamente
é atualizada para:
=C7/3,05
=C8/3,05
=C9/3,05
= ...
22
Replicando Fórmulas
• Por que a replicação de fórmulas
funciona ajustando a referência às
células nelas contidas?
– Porque a ferramenta trabalha com:
• Referência de célula relativa
• Referência de célula absoluta
23
Referência Relativa
• Indica posicionamento relativo
– Exemplos
• Uma linha para baixo na mesma coluna
• Duas linhas para cima e três colunas para a
direita
• Exemplo:
– =C4 + A3
24
Prática
• Criar uma célula que representa a
cotação do dólar no dia.
25
Referência Absoluta
• Indica posicionamento absoluto
• Usada quando é necessário BLOQUEAR
uma referência de célula de modo que ela
não se altere quando você COPIAR ou
MOVER a fórmula
• Como indicar uma referência absoluta?
– Normalmente se utiliza o símbolo $
– O símbolo $ diz: “não mude isso”
– Exemplo: $A$2
26
Bordas
• Menu Formatar -> Células
– orelha Borda
27
Trabalhando com Funções
• Os programas de planilha têm funções predefinidas
que auxiliam a escrever fórmulas freqüentemente
usadas e/ou complexas
• Ao invés de fazer:
=B2+B3+B4+B5+B6
• É mais fácil trabalhar
com a função SOMA
=SOMA(B2:B6)
28
Trabalhando com Funções
• Cuidado:
Lê-se: “até”
=SOMA(B2:B6)  Soma das células que
estão na faixa B2 até B6
=SOMA(B2;B6)  Soma B2 e B6, somente!
Lê-se: “e”
=SOMA(B4:B10;C8:C20;E12:G20)
29
Trabalhando com Funções
• Partes componentes de uma função
–
–
–
–
Nome  obrigatório
Abre parêntese  obrigatório
Argumentos  opcional
Fecha parêntese  obrigatório
• Um argumento pode ser:
– Um número, um texto, uma referência a célula, uma referência
a célula em outra planilha/pasta uma lista (= um ou mais
argumentos separados por ponto_e_vírgula)
• Exemplos:
– HOJE()
– MÉDIA(E6:E14; 7,5; SOMA(A1:D1))
– SE(teste-lógico; valor se verdadeiro; valor se falso)
30
Algumas funções ...
=ABS(número)  retorna valor absoluto
=PI()  retornas as 14 primeiras casas decimais do nro. Pi
=INT(número)  retorna parte inteira de número
=ALEATÓRIO()  retorna 0<=número<1
=SE(HOJE()=DATA(2005;4;10);"é domingo"; "não é domingo")
 retorna "é domingo“ se verdade e "não é domingo“ se
falso
=CONTAR.VAZIO(intervalo)  retorna número de células em
branco do intervalo
31
Mais funções ...
• Se A1:A5 contiver os números 10, 7, 9, 27
e 2, então:
– SOMA(A1:A5) é igual a 55
• soma todos os valores
– OU(1+1=1;2+2=5) é igual a FALSO
• verifica se um dos argumentos é verdadeiros
– MÉDIA(A1:A5) é igual a 11
• Média aritmética
– MÁXIMO(A1:A5) é igual a 27
• retorna maior valor
– MÍNIMO(A1:A5) é igual a 2
• retorna menor valor
32
Mais funções
• SE(teste_lógico;valor_se_verdadeiro;valor
_se_falso)
– SE(B2>C2;"Acima do orçamento";"OK") é igual a
"Acima do orçamento”
• CONT.NÚM(valor1;valor2; ...)
33
Mais funções ...
• CONT.SE(intervalo;critérios)
– Suponha que A3:A6 contenha "maçãs", "laranjas",
"pêras", "maçãs", respectivamente.
• CONT.SE(A3:A6;"maçãs") é igual a 2
– Suponha que B3:B6 contenha 32, 54, 75, 86,
respectivamente.
• CONT.SE(B3:B6;">55") é igual a 2
• ÉCÉL.VAZIA(VALOR)
– ÉCÉL.VAZIA(B3) é igual a FALSO
• ARRED(num; num_digitos)
• ARRED(2,15; 1) é igual a 2,2
• ARRED(2,149; 1) é igual a 2,1
• ARRED(-1,475; 2) é igual a -1,48
34
Funções aninhadas
• =SE(ÉCÉL.VAZIA(D9); "-";
SE(D9<=$B$5;“Desclassif.";“Classif."))
35
Funções financeiras: exemplo 1
(cedido pelo Prof. Roberto Cabral de M. Borges)
• Deseja-se fazer uma poupança de R$ 300,00
por mês, durante 20 meses. A taxa de juros
mensal é de 2,5% ao mês. Qual o valor total
poupado no fim do período?
Sintaxe:

Pr estação 1  taxa

VF 
taxa

VF(taxa ; período ; prestação)
= VF (2,5% ; 20 ; -300) ----> R$

período

 1

7.663,40
37
Funções financeiras: exemplo 2
(cedido pelo Prof. Roberto Cabral de M. Borges)
• Uma loja oferece um refrigerador em 10
parcelas de R$ 120,00. A loja informa que a taxa
e juros é de 4,5% ao mês. Qual o valor à vista do
produto ?
período 

Pr estação 1 1 taxa



Sintaxe: VP 
taxa


VP(taxa ; período ; prestação)
= VP (4,5% ; 10 ; -120) ----> R$ 949,53
38
Funções financeiras: exemplo 3
(cedido pelo Prof. Roberto Cabral de M. Borges)
• Qual a taxa de juros de um financiamento em
que o valor à vista é de R$ 3000,00, e vai ser
pago em 15 parcelas de R$ 340,00?
Sintaxe:


1


 período 


 ValorFuturo 

TAXA  


Valor Presente
1
TAXA(Período ; prestação ; valor presente)
= TAXA (15 ; 340 ; -3000) ----> 8 %
39
Funções financeiras: exemplo 4
(cedido pelo Prof. Roberto Cabral de M. Borges)
• Qual o valor da prestação que se pagará para
juntar R$ 8000,00 em 30 meses, a uma taxa de
juros de 3,6% ao mes?
Sintaxe:
PGTO 
Valor Pr esente * Taxa

1  1 Taxa

 período
PGTO(taxa ; período ; valor presente)
= PGTO (3,6% ; 30 ; -8000) ---->
R$ 440,44
40
Funções financeiras: exemplo 5
(cedido pelo Prof. Roberto Cabral de M. Borges)
• Quanto tempo será necessário para juntar R$ 5.000,00,
poupando R$ 250,00 por mes, a uma taxa de juros de 3,3 % ao
mes?
 

Sintaxe:
NPER 
ValorFuturo *Taxa 
ln 1  



Pr estação

 

ln 1 Taxa

NPER(taxa ; prestação ; valor presente ;valor futuro)
Se os R$5.000,00 for valor de hoje:
= NPER (0,033 ; 250 ; -5000) ----> 33,22768 ou
34 meses
Se os R$5.000,00 for o valor a se atingir:
= NPER (0,033 ; 250 ; ; -5000) ----> 15,61 ou
16 meses
41
Localizando funções
• Menu Inserir  função ou clicar em:
42
Localizando funções
• Inserindo argumentos para a função
“ARRED”
Clique aqui e c/ o
auxílio do mouse
selecione célula(s)
da planilha
43
Exercícios:
•
•
•
•
Criar uma planilha para permitir a entrada de 10 números
e calcular a quantidade de números no intervalo [10,20]
Gerar em uma planilha os 10 primeiros termos da Série de
Fibonacci, sabendo-se que os 2 primeiros termos tem
valor 0 e 1, e os demais são calculados pela expressão:
tn  tn1  tn2
Gerar em uma planilha 100 números aleatórios entre 1 e
100 e determinar a porcentagem de números pares e a
porcentagem de números ímpares
Considere a série sen(1)+sen(2)+sen(3)+...+sen(100).
Gere uma planilha com os elementos da série e calcule o
valor da série.
44
Trabalhando com Gráficos
• São criados a partir dos dados da
planilha
• Tipos de gráficos
–
–
–
–
Colunas e Barras
Linha e Dispersão (XY)
Área Empilhada, Colunas e Barras
Pizza
45
Partes de um Gráfico
Eixo de valores (y ou vertical)
Linhas de grade
Piores e Melhores casos
Área de Plotagem
Média da Prova
Melhor Tempo
ro
va
3a
.P
ro
va
Pior Tempo
2a
.P
1a
.P
ro
va
10,00
8,00
6,00
4,00
2,00
0,00
Legenda
Eixo das categorias (x ou horizontal)
Área do Gráfico
46
Gráfico
de Colunas
•São úteis quando a altura de
Um ponto específico é mais
Importante que a tendência
•Evite-os se tiver muitas
Seqüências a serem plotadas
Total em Estoque
R$ 12.000,00
R$ 10.000,00
R$ 8.000,00
R$ 6.000,00
R$ 4.000,00
R$ 2.000,00
R$ Office
2000
Windows Norton Missão
XP
AntiVírus Resgate
Guerra
nas
Estrelas
47
Gráfico de Barras
Total em Estoque
Guerra nas Estrelas
Missão Resgate
Norton AntiVírus
Windows XP
Office 2000
R$ -
R$
2.000,00
R$
4.000,00
R$
6.000,00
R$
R$
R$
8.000,00 10.000,00 12.000,00
48
Gráfico de Dispersão (XY) e
Linha
Gráfico de Dispersão
•São úteis quando tiver
muitos dados e nenhuma
Tendência específica
40,0
30,0
carvão
20,0
gasolina
óleo
10,0
0,0
1975
1980
1985
1990
1995
•O gráfico de dispersão trata
Os dados como números
2000
Gráfico de Linha
40,0
30,0
carvão
20,0
gasolina
óleo
10,0
0,0
1980 1985 1990 1995 1996 1997
49
Gráfico de Área Empilhada e
Coluna
Gráfico de Área Empilhada
•Mostram a acumulação e a
Contribuição dos dados
100,0
80,0
óleo
60,0
gasolina
40,0
carvão
20,0
0,0
1980
1985
1990
1995
1996
1997
Gráfico de Coluna Empilhada
100,0
80,0
óleo
60,0
gasolina
40,0
carvão
20,0
0,0
1980 1985 1990 1995 1996 1997
50
Gráfico de Torta
•São úteis para plotar uma
única seqüência de dados
•Permite comparar o todo e
•Suas partes
Consumo de Energia U.S. - 1997
28%
carvão
44%
gasolina
óleo
28%
51
Criando um Gráfico
• Selecione o intervalo de células que contém
os dados a serem plotados
• Selecione o tipo de gráfico
• Selecione o formato
• Inclua título, legenda, títulos p/ os eixos X
eY
• O gráfico pode ser criado:
– Incorporado à planilha
– Como um documento gráfico
52
Help no Excel
54
Exercício:
• Calcular e “plotar” os valores das
funções:
f1 ( x )  ax 2  bx  c
f 2 ( x )  ax  bx  c
para valores de x em [0,3] e valores de
a, b e c variáveis
2
55