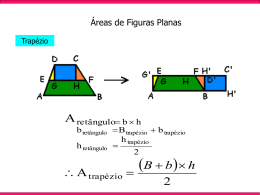
Alguns processos e procedimentos matemáticos pertinentes a atividade:
• Pensamento algébrico e espacial;
• Diferentes modos de resolução;
• Expressão escrita matemática.
Objetivos:
• Desenvolver estratégias para decompor figuras planas em várias figuras
planas congruentes;
• Relacionar o perímetro e a área de figuras planas com a representação
algébrica;
• Produzir argumentações algébricas como elemento integrador da
comunicação matemática.
1) Divida a área do trapézio retângulo, em quatro áreas congruentes.
x
x
2x
Modelos da
geométricas:
figura
original
para
realizar
algumas
investigações
1) Divida a área do trapézio retângulo, em quatro áreas congruentes.
x
x
2x
Modelos da
geométricas:
figura
original
para
realizar
algumas
investigações
Agora responda:
A) Como podemos obter a área do trapézio retângulo, sem fazer uso de
uma fórmula? Obtenha a expressão algébrica que representa esta área e
explique os procedimentos utilizados.
B) Escreva o monômio que representa a medida do lado oblíquo aos lados
paralelos do trapézio retângulo. Explique o procedimento utilizado.
C) Escreva a expressão algébrica que representa o perímetro do trapézio
retângulo.
D) Descreva pelo menos dois procedimentos para a obtenção da área de
um dos polígonos resultantes da divisão do trapézio retângulo.
Agora responda:
E) Escreva a expressão algébrica que representa o perímetro de um dos
polígonos resultantes da divisão do trapézio.
F) Verifique se existe alguma relação entre o perímetro do polígono
resultante da divisão do trapézio com o perímetro do trapézio retângulo. Em
caso afirmativo, explique tal relação.
G) Investigue outras divisões possíveis de serem realizadas com a área do
trapézio retângulo dado, mantendo a congruência entre as figuras. Com
base nestas divisões, responda: existe alguma relação entre a maior divisão
possível (menor fração de área) e as demais divisões?
Agora responda:
A) Como podemos obter a área do trapézio retângulo, sem fazer uso de
uma fórmula? Obtenha a expressão algébrica que representa esta área e
explique os procedimentos utilizados.
Dividindo-o por exemplo em um
quadrado mais meio quadrado.
x
x
x2
x2/2
2x
Área = x2 + x2/2
Área = 3x2 /2
B) Escreva o monômio que representa a medida do lado oblíquo aos lados
paralelos do trapézio retângulo. Explique o procedimento utilizado.
x
x
2x
C) Escreva a expressão algébrica que representa o perímetro do trapézio
retângulo.
Perímetro = x + x + 2x +
Perímetro = 4x +
D) Descreva pelo menos dois procedimentos para a obtenção da área de
um dos polígonos resultantes da divisão do trapézio retângulo.
1) Área = (3x2 /2) : 4 = 3x2 /8
2) Área = (x /2)2 + (x2 /2)2 / 2 = x2 /4 + x2 /8 = 3x2 /8
x /2 x /2
x /2
x /2
Agora responda:
E) Escreva a expressão algébrica que representa o perímetro de um dos
polígonos resultantes da divisão do trapézio.
F) Verifique se existe alguma relação entre o perímetro do polígono
resultante da divisão do trapézio e o perímetro do trapézio retângulo. Em
caso afirmativo, explique tal relação.
G) Investigue outras divisões possíveis de serem realizadas com a área do
trapézio retângulo dado, mantendo a congruência entre as figuras. Com
base nestas divisões, responda: existe alguma relação entre a figura
original e uma das figuras resultante da divisão?
E) Escreva a expressão algébrica que representa o perímetro de um dos
polígonos resultantes da divisão do trapézio.
x/2
x /2
x/2
Perímetro = (4x/2) +
= 2x +
x /2
F) Verifique se existe alguma relação entre o perímetro do polígono
resultante da divisão do trapézio e o perímetro do trapézio retângulo. Em
caso afirmativo, explique tal relação.
Perímetro = 2x +
Perímetro = 4x +
O perímetro do polígono resultante da divisão do trapézio
é a metade do perímetro do trapézio retângulo.
2P = 2. 2p
G) Investigue outras divisões possíveis de serem realizadas com a área do
trapézio retângulo dado, mantendo a congruência entre as figuras. Com
base nestas divisões, responda: existe alguma relação entre a figura
original e uma das figuras resultante da divisão?
2p = x +
2p = 4x +
Neste caso, não existe
relação entre os dois
perímetros.
2p = 2x +
2p = 4x +
Neste caso, não existe
relação entre os dois
perímetros.