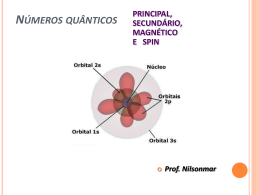
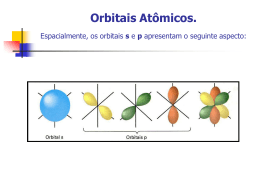
ÁTOMOS:
ESTRUTURA ELETRÔNICA
O que fazem os elétrons?
Como eles se mantém em órbita?
As leis da física eram insatisfatórias para descrever
movimento de partículas tão pequenas quanto os átomos.
Bohr propôs a elucidação da estrutura atômica pelo estudo
da natureza da luz emitida pelas substâncias a temperatura
alta ou sob influência de descarga elétrica
Melhor maneira de investigar a estrutura atômica - estudo
da interação dos átomos com a radiação eletromagnética
Propriedades das Ondas
•Todas as ondas têm um comprimento de onda
característico, , e uma amplitude, A.
•A frequência, , de uma onda é o número de ciclos que
passam por um ponto em um segundo.
•A velocidade de uma onda, v, é dada por sua
frequência multiplicada pelo seu comprimento de onda.
•Para a velocidade da luz = c = 2,99x108 m.s-1.
λ é geralmente expresso em metros (m) ou nm (visível)
ν é expressa em s-1 (hertz – Hz)
Natureza Ondulatória
Natureza Ondulatória
•A radiação eletromagnética se movimenta através do
vácuo com uma velocidade de 2,99 x 108 m/s.
•As ondas eletromagnéticas têm características
ondulatórias semelhantes às ondas que se movem na
água.
Natureza Ondulatória
Energia e Fótons
• Planck: a energia só pode ser liberada (ou absorvida) por átomos
em pacotes, chamados quantum (mais tarde denomidos fótons).
• A relação entre a energia de um fóton e a frequência é Eh

onde h é a constante de Planck (6,626  10-34 J s).
• O efeito fotoelétrico fornece evidências para a natureza de
partícula da luz - “quantização”.
Para entender a quantização, considere a subida em uma rampa
versus a subida em uma escada:
Para a rampa, há uma alteração constante
na altura, enquanto na escada há uma
alteração gradual e quantizada na altura.
Energia Quantizada e Fótons
Einstein supôs que a luz trafega em pacotes de energia
denominados fótons.
A energia de um fóton:
E  h 
hc

À medida que frequência aumenta , energia aumenta
À medida que comprimento de onda aumenta, energia diminui
PROBLEMAS NUMÉRICO
1-Os aparelhos de CD (compact disc) operam com lasers que
emitem luz vermelha com o  de 685 nm. Qual é a energia de um
fóton desta luz? h = 6,63x10-34 J.s
(nm)
( m)
2- A luz violeta tem =410nm. Qual a sua frequência? Qual é a
energia de um fóton de luz violeta? Qual a energia de 1,0 mol de
fótons violeta? Compare a energia do fóton de luz violeta com a
energia de um fóton de luz vermelha. Qual tem mais energia? Por
qual fator?
Modelo de Bohr
Bohr propôs alguns postulados:
• O elétron se move em torno de um núcleo em uma órbita fixa.
• As órbitas do elétron são restritas, isto é, nem todas órbitas são
permitidas em qualquer situação
• Os elétrons em órbita NÃO emitem energia eletromagnética.
Emissão de energia (ou absorção) ocorre somente na passagem
de níveis.
• Cada órbita tem uma energia associada, e a diferença de
energia entre dois níveis é igual à energia emitida/absorvida na
mudança.
h  E2  E1
O comportamento
ondulatório da matéria
• Sabendo-se que a luz tem uma natureza de partícula, parece
razoável perguntar se a matéria tem natureza ondulatória.
• Utilizando as equações de Einstein e de Planck, De Broglie propôs
que todo tipo de matéria apresenta propriedades ondulatórias:
h

mv
O momento, mv, é uma propriedade de partícula, enquanto λ é uma
propriedade ondulatória.
• De Broglie resumiu os conceitos de ondas e partículas, com efeitos
notáveis se os objetos são pequenos.
• Considere uma bola (0,150 Kg) se movendo a 41,6 m/s
6,626x1034 J / s

(0,150Kg )(41,6m / s )
J  Kgm2 s  2
6,626x1034 Kgm2 s  2 / s

 1,06x1034 m Fora do espectro
(0,150Kg )(41,6m / s )
eletromagnético
• Um elétron na mesma velocidade:
6,626x1034 J / s

(9,109x1031 Kg )(41,6m / s )
J  Kgm2 s  2
6,626x1034 Kgm2 s  2 / s
5


1
,
75
x
10
m Região IV
31
(9,109x10 Kg )(41,6m / s )
O princípio da incerteza
O princípio da incerteza de Heisenberg: na escala de massa
de partículas atômicas, não podemos determinar exatamente a
posição, a direção do movimento e a velocidade
simultaneamente.
•Para os elétrons: não podemos determinar seu momento e sua
posição simultaneamente.
Nova abordagem da estrutura atômica leva em conta natureza
ondulatória do elétron, seu comportamento é descrito em
termos apropriados para ondas.
Modelo descreve precisamente a energia do elétron e define
sua localização em termos de probabilidades.
Mecânica quântica e
orbitais atômicos
• Schrödinger propôs uma equação que contém os termos onda e
partícula.
• A resolução da equação leva às funções de onda (ψ).
• A função de onda fornece o contorno do orbital eletrônico.
• O quadrado da função de onda fornece a probabilidade de se
encontrar o elétron, isto é, dá a densidade eletrônica para o átomo.
Mecânica quântica e
orbitais atômicos
Mecânica quântica e
orbitais atômicos
Orbitais e números quânticos
•
•
•
Se resolvermos a equação de Schrödinger, teremos as funções de
onda e as energias para as funções de onda.
Chamamos as funções de onda de orbitais.
A equação de Schrödinger necessita de três números quânticos:
1. Número quântico principal, n. Informa a respeito da energia
do orbital. À medida que n aumenta, o orbital torna-se maior
e o elétron passa mais tempo mais distante do núcleo. n pode
ser qualquer número inteiro de 1 a 
Mecânica quântica e orbitais atômicos
Mecânica quântica e orbitais atômicos
Orbitais e números quânticos
•
•
•
Os orbitais podem ser classificados em termos de energia para
produzir um diagrama de Aufbau.
Observe que o seguinte diagrama de Aufbau é para um
sistema de um só elétron.
À medida que n aumenta, o espaçamento entre os níveis de
energia torna-se menor.
Mecânica quântica e orbitais atômicos
Orbitais e números quânticos
Representações dos orbitais
Orbitais s
•
•
Todos os orbitais s são esféricos.
À medida que n aumenta, os orbitais s ficam maiores.
Representações dos orbitais
Orbitais p
•
•
•
•
•
•
Existem três orbitais p, px, py, e pz.
Os três orbitais p localizam-se ao longo dos eixos x-, y- e z- de um
sistema cartesiano.
As letras correspondem aos valores permitidos de ml, -1, 0, e +1.
Os orbitais têm a forma de halteres.
À medida que n aumenta, os orbitais p ficam maiores.
Todos os orbitais p têm um nó no núcleo.
Representações dos orbitais
Orbitais p
Representações dos orbitais
Orbitais d e f
•
•
•
•
•
Existem cinco orbitais d e sete orbitais f.
Três dos orbitais d encontram-se em um plano bissecante aos eixos
x-, y- e z.
Dois dos orbitais d se encontram em um plano alinhado ao longo
dos eixos x-, y- e z.
Quatro dos orbitais d têm quatro lóbulos cada.
Um orbital d tem dois lóbulos e um anel.
Representações dos orbitais
Representações dos orbitais
•
Elétron comporta-se como se tivesse uma rotação, como a Terra.
•
A descrição completa de um elétron em um átomo requer quatro
números quânticos: n, l, ml, ms
Atribuição dos elétrons
Configuração eletrônica dos íons
• Para formar um cátion a partir de um átomo neutro, um ou
mais elétrons de valência são removidos:
Na: 1s2 2s2 2p6 3s1
Na+: [1s2 2s2 2p6 ]+ eÁtomos e íons com elétrons desemparelhados são
paramagnéticos (podem ser atraídos por um campo
magnético). Do contrário são ditos diamagnéticos.
• Exercícios
1- Dê a configuração eletrônica do enxofre, usando as notações spdf, do gás
nobre e de orbitais em caixas. Z=16
2- Dê a configuração eletrônica do cobre, e dos seus íons +1 e +2. Algum
desses é paramagnético? Quantos elétrons desemparelhados há em cada
um deles? Z=29
3- Utilizando a configuração eletrônica condensada para elétrons mais internos
e de quadrículas para elétrons de valência, determine o número de elétrons
desemparelhados nos seguintes átomos:
Ti - (Z=22)
Ga - (Z=31)
Rh - (Z=45)
I - (Z=53)
4- Dê a configuração de orbitais em caixas para K+ e Cl-.