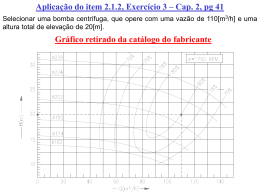
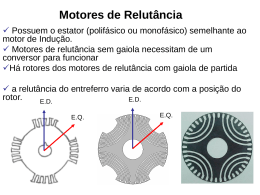
Equação Fundamental para
máquinas hidráulicas
As aletas do rotor impõem uma variação da quantidade de
movimento angular do escoamento de líquido, que reage exercendo
um torque sobre o rotor. O rotor gira a velocidade angular constante (nrpm), o que implica na existência de uma potência disponível;
  T,
W
T é o torque e é a velocidade angular do rotor (radiano/tempo), igual a
(2n) sendo n a rotação, número giros na unidade de tempo.
No desenvolvimento da Equação Fundamental para as turbinas ou
bombas serão usadas "equações idealizadas", que não representarão
os processos reais do escoamento do fluido (e da transferência de
energia) através do rotor.
No desenvolvimento da Equação Fundamental para as turbinas
ou bombas serão usadas "equações idealizadas", que não
representarão os processos reais do escoamento do fluido (e da
transferência de energia) através do rotor.
Hipóteses:
•
No processo de transferência de energia do rotor ao fluido de
trabalho, não há qualquer tipo de perda, sejam elas, perdas
hidráulicas, volumétricas ou mecânicas.
W  W
 útil  T ,
toda a potência de eixo do rotor da bomba é potência útil, ou seja,
é efetivamente transferida ao fluido de trabalho.
W
 gH  gQ H

m
útil
onde
E combinando as duas equações tem-se:

H
T

mg

  ρQ
m
Da Equação de Conservação do Momento Angular, temos que, para um
escoamento permanente, o fluxo líquido de quantidade de movimento
angular através de uma superfície de controle é igual a um torque, portanto
para se obter uma equação para o toque T deve-se aplicar esta equação à
um Volume de Controle que envolva o rotor da bomba.
• O rotor da bomba é formado por infinitas aletas, que têm espessura
desprezível, isto é, z =  e s 0, sendo z o número de aletas do
rotor de uma bomba e s a espessura média destas aletas;
A idéia é a de que o escoamento relativo do fluido de trabalho,
sendo unidimensional, seja determinado exatamente pela curvatura
das aletas, em todo o seu percurso através do rotor;
Pode-se, então, afirmar que o vetor velocidade relativa do fluido
de trabalho é sempre tangente à aleta, em qualquer ponto do
escoamento através do rotor.
Para se aplicar a Equação de Conservação do Momento Angular, é
necessário conhecer a velocidade absoluta do escoamento através do rotor.
A velocidade relativa do escoamento é conhecida (em direção e sentido), em
qualquer posição radial entre as arestas de entrada e saída do rotor, assim como a
velocidade do rotor (velocidade tangencial, u), desde que a velocidade angular seja
especificada, assim como as dimensões geométricas do rotor.
Consequentemente, a velocidade absoluta do fluido de trabalho, C, pode
ser obtida da composição vetorial das velocidades relativa w, do fluido, e
absoluta u, do rotor, em posições radiais genéricas
Onde:
– W é a velocidade relativa do fluido de trabalho;
– C sua velocidade absoluta.
– A região da entrada do rotor está indicada pelo subscrito 4 e a de saída,
pelo subscrito 5.
– Assim, u4, W4, e C4, são as velocidades na entrada do rotor e u5 W5, e
C5, são as velocidades na saída do rotor;
–  o ângulo entre a velocidade relativa e a direção tangencial, medido em
sentido oposto ao giro do rotor;
–
o ângulo entre a velocidade absoluta e a direção tangencial.

Esta composição vetorial forma os triângulos de velocidade do escoamento
na entrada e saída do rotor.
w
1
w4
w4
w1
4
4


4
u1
u4
vv5
2
w2
w5
5
4
u1
u4
vv5
2 w
2
w5

5

5
u5
u2
5
u2
u5

está fixado a partir do momento em que se define a curvatura das pás (o
projeto do rotor) das aletas, da entrada até a saída do rotor. O ângulo , é função
das características operacionais da bomba (rotação e vazão, entre outras). Isto é,
se há variação de rotação da bomba, há variação do ângulo  , pois a alteração
da velocidade tangencial do rotor, ou a vazão da bomba, altera o triângulo de
velocidades.
Com a definição das velocidades do escoamento, e os ângulos que elas
formam, pode-se então formular uma equação para o torque da bomba, em função
das variáveis operacionais e características de projeto do rotor da bomba.
Aplicando-se Equação da Conservação da Quantidade de Movimento
Ângular, temos que:
 C5 r5 cosα5  C4 r4 cosα4
Tm
Como: H 

T

mg
Então:
H

g
m
C r cosα  C r

m
5
5
5
4

cos α4  
4



cos α   C r
C
r
g
5
5
5
4
4

cos α4 
Como o escoamento é idealizado, devemos mudar a nomenclatura da
altura de elevação real para altura de elevação teórica infinita:
H  Ht 
Onde, o subscrito t indicando um processo sem perdas (1ª idealização), e
 representando o escoamento através do rotor com número infinito
o subscrito
de aletas, com espessura muito pequena (2ª idealização).
H
t


g
m


 C5 r5 cosα5   C4 r 4 cosα4   
m

g
C r
5
5

cosα5   C4 r 4 cosα4 
Lembrando que + representa máquinas geradas e – representa
máquinas motoras.
A equação acima, estabelece que a energia específica que o rotor transfere
ao fluido varia proporcionalmente com a velocidade angular (quanto mais
rapidamente gira o rotor, maior a quantidade de energia transferida). Os dois
termos entre parênteses têm sinal invertido, e suas contribuições à quantidade
de energia transferida são opostas assim a quantidade de energia específica
transferida ao fluido será máxima quando o termo negativo for nulo, isto ocorre
quando o ângulo α4, for igual a 90º.
Geralmente não é o que ocorre na região de entrada do rotor, nos
escoamentos reais, mas o ângulo α4 é, quase sempre, muito próximo de 90º,
fazendo com que o termo negativo, seja próximo de zero, podendo ser
desprezado quando comparado ao fluxo de quantidade de movimento angular na
saída do rotor
Com α1 próximo de 90º, a equação simplifica-se para:
H
t

u

,
C
g  u5 
5
Onde Cu5 = C5 cosα5 (componente tangencial da velocidade absoluta do fluido
de trabalho na aresta de saída do rotor).
Assim, quanto maior a velocidade angular de rotação do rotor de uma
bomba, e quanto maior o rotor da bomba maior será u5, e consequentemente
maior será C5u , fazendo com que a altura de elevação H t da bomba seja
maior.
De forma similar ao que acontece numa bomba, numa turbina se tivermos
α5 com valor próximo de 90º, a equação para a turbina, simplifica-se para:
H
t

u  ,
g C
4
u4
Estas são formas idealizadas e simplificadas da Equação Fundamental
de bombas, turbinas e ventiladores em geral. Entretanto, a formulação
resultante não mostra, explicitamente, características de projeto do rotor, e
mesmo condições operacionais das máquinas de fluxo em geral).
A componente tangencial da velocidade absoluta, Cu5, pode ser escrita
em termos da componente radial, Cm5, conforme o triângulo de velocidades,
assim como Cu4, pode ser escrita em termos da componente radial, Cm4:
Do Triângulo de Velocidades temos que:
C
U5
 u5  Wu5  u5  Cm5 ctg β
5
Substituindo na Equação Fundamental torna-se:
H
t

u   u  
g C
g u C
5
5
u5
5
m5
ctgβ
5

Cm5 pode ser expressa em termos da vazão em volume que a bomba
descarrega, Q , aplicando-se a Equação de Conservação da Massa ao mesmo
Volume de Controle.
Aplicando a Equação da Conservação da Massa, a vazão é dada por:
Q  2  π  r4  b 4  f 3 Cm4  2  π  r5  b 5  f 6 Cm5
Onde b4 e b5 são as alturas na aresta de entrada e saída do rotor, e f3 e f6 são
os coeficientes de estrangulamento na entrada e saída do rotor.
b5
canal do rotor
aresta de saída
r5
r4
aresta de entrada
largura b4
eixo da bomba
Com isso Cm4 e Cm5 podem ser expressos por:


Q
Q
C m5 
C m4 
2  π  r5  b 5
2  π  r4  b 4
E a Equação Fundamental será escrita como:
H t


u5 
Q
  u 5 
 ctgβ 5 
g 
2  π  r5  b 5

Como o ângulo β5 determina a forma da dependência: se é uma
dependência direta, ou uma dependência inversa, então se β5 > 90º, a altura de
elevação aumenta linearmente com o aumento da vazão em volume; se β5 <
90º, a altura de elevação diminui linearmente com a diminuição da vazão e se
b5 = 90º , a altura de elevação não varia com a vazão.
A curva característica de uma máquina de fluxo é, por definição, a
curva que representa a dependência que existe entre a quantidade de
energia transferida pela máquina (real ou idealizada) e a vazão do fluido de
trabalho.
Para a equação idealizada tem-se 3 possibilidades de acordo com o valor
do ângulo β 5, está mostrada na curva característica idealizada, a seguir.
Htoo
r , b e n dados
5 5
> 90º
5
u2
5 /g
= 90º
5
< 90º
2
Q
( 2 r 5 b 5 u 5 ) / ctg 
5
À medida em que a vazão aumenta, é de se esperar que, nos escoamentos
reais (viscosos), a energia dissipada (em perdas hidráulicas, por exemplo)
aumente com o quadrado da vazão. Assim, uma parcela substancial da potência
disponível no eixo é irreversivelmente dissipada em perdas, e a energia
específica transferida não pode, aumentar, ou mesmo se manter constante, com
o aumento da vazão.
A influência da magnitude do ângulo β5 sobre a curva característica da
bomba, e sobre as formas construtivas dos das aletas dos rotores, deve ser
objeto de análise.
As bombas centrífugas quase sempre apresentam rotores de aletas
curvadas para trás em relação ao sentido de rotação do rotor, isto é, β5 < 90º, e
os valores usuais estão por volta dos 30º.
Em ventiladores, por outro lado, dependendo das características
operacionais exigidas pela instalação, pelo porte do equipamento, pela
responsabilidade da instalação, etc, encontram-se as mais variadas
configurações de aletas, curvadas para trás, curvadas para a frente, retas e
inteiramente radiais, e aletas curvadas com ângulo de saída β5 = 90º.
Nos triângulos de velocidade, que as componentes radiais da
velocidade absoluta de saída têm aproximadamente a mesma magnitude,
se a largura do rotor for a mesma para todos os casos, a vazão
descarregada por cada um deles é aproximadamente a mesma.
Assim, se as grandezas geométricas são semelhantes, e as
características operacionais (vazão e rotação) são aproximadamente iguais,
a maior velocidade C5 do rotor, que tem β5 > 90º, resulta somente do seu
desenho (curvatura). E quanto maior a velocidade, maior a dissipação
viscosa do escoamento, implicando em menor eficiência no processo de
transferência de energia no rotor da bomba. Consequentemente, da
potência de eixo da bomba, uma parcela considerável será dissipada em
perdas hidráulicas se o rotor tiver β5 > 90º.
Equação fundamental ou de
Euler
Hipóteses
•
•
•
•
•
Infinitas pás.
Espessura das pás infinitesimal.
Fluido incompressível.
Fluido ideal, sem atrito.
Entrada sem choque do escoamento sobre as
pás.
• Escoamento permanente.
• Escoamento irrotacional.
• Escoamento mono-dimensional .
Considerações
• Escoamento unidimensional (apenas a componente “x” da força).
• Vazão “dQ”.
• aplicando o principio das quantidades de movimento na linha média
LL´(momento angular).
Figura
b2
canal do rotor
aresta de saída
r2
r1
aresta de entrada
largura b1
eixo da bomba

dVX
dFx  dm
dt
Desenvolvimento da fórmula
• 1º-Após substituir m= Vvol e dQ= dVvol /dt o volume será dado por
dVvol =dQ dt.Portanto a massa será dm =  dQ dt

dV
dVX
dFx  dm X  ρ dQ dt
dt
dt
• 2º-Integrando esta equação com relação à velocidade desde os
pontos 4 e 5, onde ela passará a se chamar de C4 e C5, tem-se

5
dFx  ρ dQ  dVx  ρ dQ(C5  C 4 )
4
• 3º-Aplicando o momento angular da quantidade de movimento
em relação ao eixo do rotor

dM  dFx L  ρ dQ(L5C5  L4 C4 )
• 4º-Integrando-se novamente
Mt   ρ Q(L5C5  L4C4 )
• Para se obter a potência multiplicamos pela velocidade angular.
Pt  w.M t   wρ Q(L5 C5  L 4 C4 )
A partir da figura , L5= r5cos5 e L4= r4cos4
Pt  wρ Q(L5 C5  L 4 C4 )  wρ Q(C5 cosα 5 r5  C4 cosα 4 r4 )
C5.cos5= Cu5
wr5 = u5
C4.cos4= Cu4
wr4 = u4
Pt  wρ Q(C5 cosα 5 r5  C4 cosα 4 r4 )  ρ Q(Cu5 u 5  Cu4 u 4 )
Pt  ρ Q(Cu5 u 5  Cu4 u 4 )  γQHt
Finalmente a equação de Euller onde o sinal de + é para
máquinas motoras e o sinal de menos é para geradoras.(vale para
máquinas axiais e radiais.
1
H t   (u 5 C u5  u 4 C u4 )
g
Maquinas Hidráulicas Motoras
• Procura-se tender o Cu5 a zero e α5=90°
1
Ht   u 4Cu 4
g
1  C 24  C 52
Ht   
g 
2
  u 24  u 52

  2
 
  W52  W42

 
2
 




Maquinas Hidráulicas Geradoras
• Procura-se tender o Cu4 a zero e α4=90°
(quando utilizamos aletas direcionais na
entrada, o α4 pode ser diferente de 90°)
1
Ht   u 5Cu 5
g
1  C 52  C 24   u 52  u 24   W42  W52


Ht   


 
g 
2
2
2
 
 




Utilizando Bernoulli
• Sinal “+” para máquinas geradoras e “-” para máquinas
motoras.
p p C C
H   ρg  2g  Z5  Z4 
5
4
2
2
5
4
t
COMPARANDO a equação de Bernoulli com a de Euller e
fazendo Z4=Z5 temos:
ΔHest   
p p
5
ρg
4
1  u 52  u 24
   g  2

1  C 52  C 24
  
din
g 
2
ΔH




  W42  W52

 
2
 




A forma do rotor e o grau de reação
• A forma do rotor e suas aletas influi diretamente no grau de reação.
• O grau de reação ( representa a fração da energia total que é
transferida no rotor sob a forma de variação de pressão.
• Rearranjando a equação para Z4=Z5 tem-se:
H
p p C C


2
t
1
ρg
2
2
5
4
2g
 ΔH est  ΔH din
Hest (altura de pressão) , Hdin (altura dinâmica)
• Dividindo-se todos os termos da equação acima por Ht e
rearranjando temos o grau de reação.
ρ t  Hest  1  Hdin  1 -
H
t
H
t
Para maquinas geradoras
CU5
2U5
ρ t  Hest  1  Hdin  1 -
H
t
H
t
CU4
2U4
Para maquinas motoras
Máquinas de Ação e Reação
Utilizando a equação da altura de pressão
ΔHest   
p p
5
4
ρg

Para máquinas Geradoras : O grau de reação varia 0  t  1
• Hest = 0 p5 = p4 máquina de ação (sem aplicação)
• Hest  0
máquina de reação (bombas axiais e radiais)
Para máquinas Motoras : O grau de reação varia 0  t  1
• Hest = 0
• Hest  0
p5 = p4 máquina de ação (turbina pelton)
p5 ≠ p4 máquina de reação (turbina francis/kaplan)
Diferença quadrática das velocidades
• Desenvolvendo a equação do grau de reação, e expressando em
termos das características geométricas do rotor temos:
C5  C4  Cu5  Cm5  cu4  cm4
2
2
2
2
2
2
• Considerando b4 = 90º , Cu4 = 0 (máquinas de fluxo)
C5  C4  Cu5  Cm5  cm4
2
2
2
2
2
• Mantendo-se a velocidade meridional constante ou canais de seção
transversal do rotor constantes (Cm4 = Cm5)
C C  C
2
2
2
5
4
u5
• Desenvolvendo a equação do grau de reação chegamos a uma
nova equação.(para Cm4 = Cm5 , b4 = 90º e Cu4 = 0)
 H
H
ρ t
est
t
C 2 u5
 12gH t
• Desde que Cu5  u5  Cm5 ctg β5 podemos reescrever a equação da
seguinte forma:
H
H
est
t
 1 C
2u
u5
5

1 
C
m5 
 1 
,
2
tg
 u 5 β5 
ANÁLISE:
• Quanto maior (cm5/u5 ) e menor o ângulo β5 , maior será o grau
de reação da bomba.
• Quanto menor o ângulo β5 maior será a taxa de transferência de
energia cinética, ocasionando maiores velocidades na saída do
rotor, o que gera perdas viscosas reduzindo a eficiência.Neste caso
o grau de reação da bomba é reduzido.
Neste caso, tem-se maiores velocidades do
escoamento na saída do rotor, o que implica em
maiores perdas viscosas, e menor eficiência do
equipamento, como já se discutiu (volte aos triângulos
de velocidade característicos de cada forma do rotor e
curvatura das aletas)
O grau de reação de uma máquina de fluxo está assim
associado à forma do rotor, e à eficiência no processo
de transferência de energia:
Ângulo de saída, 2
90º
= 90º
90º
Grau de reação,
Hp/Ht
1/2
= 1/2
1/2