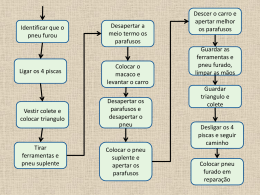
Estruturas de Dados,
Algoritmos e Complexidade
Katia Guimarães
Algoritmos
Algoritmo é um processo sistemático para a
resolução de um problema.
Algoritmo é uma seqüência finita de passos bem
definidos que levam à execução de uma tarefa.
Exemplo clássico: Receita culinária
 Note que a noção de “bem-definido” é em si
mesmo vaga. Ex: Mexer até ficar consistente.
 A palavra algoritmo não tem acento.
Ex: Algoritmo para Trocar um Pneu
1. Folgar os parafusos do pneu a ser trocado
2. Instalar o macaco e levantar o carro do lado
do pneu a ser trocado.
3. Remover completamente os parafusos do
pneu e retirá-lo do suporte.
4. Remover o pneu estepe do local onde é
guardado, colocar o pneu no suporte e
recolocar os parafusos.
5. Baixar o carro ao nível da rua.
6. Apertar os parafusos.
7. Guardar o pneu retirado, o macaco e demais
ferramentas.
Algoritmos
Note
1. Pré-suposições do algoritmo
Existem operações que você já sabe fazer, que
podem ser básicas ou mais elaboradas.
2. Nível de detalhamento
PASSO 2: Instalar o macaco e levantar o carro do
lado do pneu a ser trocado.
1. Tire o macaco da mala.
2. Instale o macaco sob o carro próximo ao pneu
a ser trocado.
3. Se o carro está em local ladeiroso, colocar um
suporte de madeira para evitar que ele se mova.
4. Alavanque o macaco até que haja espaço para o
pneu estepe entrar.
Algoritmos Computacionais
Entrada: Dados inicialmente conhecidos, os quais
permitem encontrar a solução do problema.
Saída: Resultado obtido pelo processamento de uma
entrada específica (instância).
Entrada
Algoritmo
Saída
Definição alternativa de Algoritmo Computacional:
Procedimento que transforma dados em informação.
Algoritmos Computacionais
Aspectos Básicos
1. Correção: Consiste em verificar a exatidão do
método, o que é realizado através de uma prova
usando as premissas do problema.
Ex. - Todos os valores da entrada são positivos;
- A entrada está em ordem alfabética.
2. Complexidade: Visa a obtenção de parâmetros que
possam avaliar a eficiência do algoritmo em termos
de recursos computacionais (tempo de execução,
memória ocupada, no. de nós se processamento
distribuído).
Algoritmos versus Programas
1. Especificação do problema: Entendimento das relações
existentes entre os dados que são relevantes para o problema
(estruturação lógica).
2. Projeto em alto nível: Que transformações deverão ser
efetuadas - algoritmo - para resolver o problema.
3. Refinamento e codificação: Refinar o item 2 em termos dos
mecanismos disponíveis na linguagem em que o programa
será codificado.
4. Verificação de Comportamento: Avaliar o programa obtido
para ver se satisfaz as especificações do problema e se tem bom
desempenho (tempo e memória), modificando-o, se for o caso.
Algoritmos e Estruturas de Dados
versus Complexidade
A escolha de estruturas de dados e das operações
realizadas são fatores decisivos na eficiência do
programa final.
O conhecimento de princípios de complexidade
computacional é requisito básico para a escolha
correta das estrutura de dados e dos algoritmos
mais adequados a cada problema.
Como Avaliar a Eficiência?
• Métodos Empíricos - O tempo de execução é
obtido através da execução propriamente dita
do algoritmo, considerando-se entradas diversas.
(Depende fortemente de tecnologia.)
• Métodos Analíticos – O tempo de execução é
expresso através de expressões matemáticas que
traduzem o comportamento do algoritmo em
termos do tamanho da entrada. Entre entradas de
mesmo tamanho que usam tempos de execução
diferentes, considera-se sempre o pior caso.
O Que é Tamanho da Entrada?
• Ordenação: Número de itens a ordenar.
(Tamanho n do vetor para ordenar).
• Multiplicação de 2 inteiros: Número total
de bits necessários para representar a
entrada em notação binária.
• Multiplicação de matrizes: Número de
linhas e de colunas das duas matrizes.
Exemplo de Análise de Complexidade
Algoritmo Somatório(A: array de inteiros, tam=n)
Início
|
soma = 0;
| Tempo constante
i = n;
repetir os comandos
| Trecho realizado
soma = soma + A[i];
| algumas vezes.
i = i - 1;
| Quantas?
n
até que i = 0;
output (soma) | Tempo constante
Fim
Tempo execução = Cte. + _______________________
(tsom+tatr+tsub+tcomp) * n
Cte.2
Outro Exemplo de Análise
Algoritmo Inversão de seqüência
Entrada: Elementos armazenados no vetor S[i], i=1..n.
Saída: Sequência invertida dos elementos de S[i].
Início
Para i = 1 .. n/2 faça
temp = S[i]
i
1 2
3
4 …
S[i] = S[n–i+1]
n–i+1 n n-1 n-2 n-3 …
S[n–i+1] = temp
Fim
Laço é executado n/2 vezes.
A cada iteração é feita uma troca.
Ao final a seqüência está invertida.
Tempo de execução: (toperações) * n/2.
Observando os Tempos de Execução
Algoritmo Somatório:
Cte. + (tsom+tatr+tsub+tcomp) * n = C1 + C2 * n
Algoritmo Inversão de Seqüência
(toperações) * n/2 = C3 * n/2
O que importa:
Ambos os algoritmos são LINEARES
Observando os Tempos de Execução
Gostaríamos de substituir as funções encontradas
por uma função mais simples, que tenha o mesmo
crescimento assintótico.
C1 + C2 * n
 n
C3 * n / 2
 n
Se a função tem termos de ordem diferente,
gostaríamos de capturar o termo de mais
alta ordem: 6 n3 + 4n + 9  n3
Notação que Captura esta Noção
Em complexidade computacional usamos
uma notação que em funções do tipo
C1 + C2 * n ou
C3 * n/2
ignora as constantes
- Aditivas (como C1)
- Multiplicativas (como C2, C3 e 1/2)
Ex: Se número de passos = 3n
dizemos que o tempo de execução é O(n).
Notação que Captura esta Noção
Esta notação também despreza termos de
ordem menor.
Ex: Se número de passos = n2 + n
dizemos que o tempo de execução é O(n2).
O objetivo é ressaltar o termo
que domina a curva da função.
Notação O - Definição Formal
Sejam f e h funções positivas de variável inteira n.
Diz-se que f é O(h), escrevendo-se f = O(h),
quando existirem
- Uma constante c > 0 e
- Um valor inteiro n0, tais que:
n > n0  f (n)  c . h(n)
Dois detalhes:
1. n > n0  A definição desconsidera entradas
de tamanho pequeno.
2. Para entradas arbitrariamente grandes, a
diferença entre o valor das duas funções é
no máximo uma constante multiplicativa c.
Detalhe 1: O significado de n0
n > n0  A definição desconsidera
entradas de tamanho pequeno.
90
5n+3
80
n+30
70
60
50
40
30
20
10
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
Detalhe 2: O Significado de c
140
120
n+18
4n
n^2
4(n^2)
100
4 vezes
80
60
40
20
4 vezes
0
1
2
3
4
5
6
7
Detalhe 2: O Significado de c
140
120
n+18
4n
n^2
4(n^2)
100
4 vezes
80
60
40
20
4 vezes
0
1
2
3
4
5
6
7
Note que, embora
aparentemente a
distância entre as
curvas rosa e azul
no início não seja
grande, quando n
cresce
arbitrariamente, a
distância entre elas
não pode ser
definida por uma
constante.
Como identificar se há existe uma tal constante ou não?
Calculando lim (f(n)/g(n)) e lim (g(n)/f(n)).
n→∞
n→∞
Exemplos de Notação O
f = n2 – 1  f = O(n2)
f = n2 – 1  f = O(n3)
f = 403
 f = O(1)
f = 3n + 5 log n + 2  f = O(n)
f = 52n + 5n10 
f = O(2n)
Uso da Notação O
Limite superior para o tempo de execução de um
algoritmo.
INTERPRETAÇÃO: “Algoritmo A executa em
tempo (f) no máximo uma constante vezes h.”
Relembrando a definição:
Sejam f e h funções positivas de variável inteira n.
Diz-se que f é O(h) quando existirem
- Uma constante c > 0 e
- Um valor inteiro n0, tais que:
n > n0  f (n)  c . h(n)
A Notação Simétrica Ω
Definição (notação  ): Sejam f e h funções
positivas de variável inteira n. Diz-se que f é (h),
escrevendo-se f = (h), quando existirem
- Uma constante c > 0 e
- Um valor inteiro n0, tais que:
n > n0  f(n)  c . h(n)
Uso da notação Ω:
Limite inferior para o tempo de execução.
“O problema X requer pelo menos tempo h.”
A Notação Ω
Ex:
f = n2 – 1
 f = (n2)
f = (n)
f = (1)
Mas não vale: f = (n3)
A Notação Θ
Se f = O(h) e f = Ω(h), dizemos que f = Θ(h),
ou seja, f é da ORDEM EXATA de h.
“Algoritmo A executa em tempo no máximo h.”
e
“O problema X requer pelo menos tempo h.”
Logo, o tempo de execução é ótimo.
Pior Caso
Muitas vezes o tempo de execução de um
algoritmo não depende apenas do tamanho
da entrada, mas depende também do
conteúdo da entrada.
Se um algoritmo toma tempos diferentes para
entradas do mesmo tamanho, em geral
consideramos sempre o pior caso, ou seja,
o tempo que o algoritmo gasta na pior
entrada de tamanho n.
Caso Médio
Para alguns algoritmos em particular, o tempo
de execução de um algoritmo não depende
muito do conteúdo da entrada.
Nestes casos, muitas vezes nós consideramos
o tempo médio de execução, ou seja, a
média dos tempos de execução para todas as
entradas de um mesmo tamanho.
Leitura Sugerida
 Cap. 3 de Udi Manber:
Analysis of Algorithms
Sugestão: Faça exercício 3.5.
 Caps. 1 e 2 de T. Cormen et al.
1. Introduction (Analysing Algorithms)
2. Growth of Functions