Estruturas de Dados,
Algoritmos e Complexidade
Katia Guimarães
Conteúdo Programático
• Conceitos básicos: Algoritmos, procedimentos,
funções, compilação vs. Interpretação,
complexidade de computação, notação
assintótica.
• Algoritmos em grafos – Conectividade, biconectividade, árvore geradora de peso mínimo,
distâncias, fluxo, problemas NP-completos
(Clique, cobertura, etc.)
• Caracterização e abordagens para problemas
NP-completos
Conceitos Básicos
• Algoritmos - Processo sistemático para a solução
de um problema.
• Procedimentos – Algoritmos curtos, visando a
execução de tarefas simples, muitas vezes
repetitivas. Ex:
• Funções - Procedimentos que retornam valores.
Ex: Fatorial(n)
Conceitos Básicos
• Linguagem de programação
Linguagem bem menos sofisticada que a
linguagem natural (Ex. Português), capaz de
expressar os comandos que se deseja executar
de forma que o computador possa compreender.
Característica importante: Não ambigüidade
• Compilação vs. Interpretação
Algoritmos
Algoritmo é um processo sistemático para a
resolução de um problema.
Algoritmo é uma seqüência finita de passos bem
definidos que levam à execução de uma tarefa.
Exemplo clássico: Receita culinária
 Note que a noção de “bem-definido” é em si
mesmo vaga. Ex: Mexer até ficar consistente.
 A palavra algoritmo não tem acento.
Algoritmos
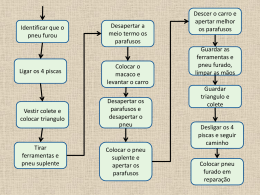
Ex: Algoritmo para trocar um pneu
1. Folgar os parafusos do pneu a ser trocado
2. Instalar o macaco e levantar o carro do lado do
pneu a ser trocado.
3. Remover completamente os parafusos do pneu e
retirá-lo do suporte.
4. Remover o pneu estepe do local onde é guardado,
colocar o pneu no suporte e recolocar os parafusos.
5. Baixar o carro ao nível da rua.
6. Apertar os parafusos.
7. Guardar o pneu retirado, o macaco e demais
ferramentas.
Algoritmos
Note
1. Pré-suposições do algoritmo
Existem operações que você já sabe fazer, que
podem ser básicas ou mais elaboradas.
2. Nível de detalhamento
PASSO 2: Instalar o macaco e levantar o carro do
lado do pneu a ser trocado.
1. Tire o macaco da mala
2. Instale o macaco sob o carro próximo ao pneu
a ser trocado.
3. Se o carro está em local ladeiroso, colocar um
suporte de madeira para evitar que ele se mova.
4. Alavanque o macaco até que haja espaço para o
pneu estepe entrar.
Algoritmos Computacionais
Entrada: Informações inicialmente conhecidas e que
permitem encontrar a solução do problema.
Saída: Resultado obtido pelo processamento de uma
entrada específica (instância).
Entrada
Algoritmo
Saída
Definição alternativa de Algoritmo Computacional:
Procedimento que transforma dados em informação.
Algoritmos Computacionais
Aspectos Básicos
1. Correção: Consiste em verificar a exatidão do
método, o que é realizado através de uma provas
formais usando as premissas do problema.
Ex. - Todos os valores da entrada são positivos;
- A entrada está em ordem alfabética.
2. Complexidade: Visa a obtenção de parâmetros que
possam avaliar a eficiência do algoritmo em termos
de recursos computacionais (tempo de execução,
memória ocupada, no. de nós se o processamento
for distribuído).
Algoritmos vs. Programas
1. Especificação do problema: Entendimento das relações
existentes entre os dados que são relevantes para o problema
(estruturação lógica).
2. Projeto em alto nível: Que operações/transformações deverão
ser efetuadas pelo algoritmo para resolver o problema.
3. Análise de alternativas.
4. Refinamento e codificação: Refinar o item 2 em termos dos
mecanismos disponíveis na linguagem em que o programa
será codificado.
5. Verificação de Comportamento: Avaliar o programa obtido
para ver se satisfaz as especificações do problema e quanto ao
desempenho (tempo e memória), modificando-o se for o caso.
Três Pontos Importantes
1. Estruturas de Dados
Representam os dados, retratando as relações
lógicas entre eles (como um modelo matemático
para a realidade do problema).
2. Operações
Manipulam estas estruturas de dados gerando
novas estruturas
3. Estruturas auxiliares
Armazenam dados relevantes para a solução
do problema. (Servem como um bloco de notas.)
Conclusão
A escolha de estruturas de dados, suas operações
e representações podem ser fatores decisivos na
eficiência do programa final.
Complexidade vs. Algoritmos e Estruturas de Dados
O conhecimento de princípios de complexidade computacional é requisito básico para a escolha correta
da estrutura de dados adequada a cada problema.
Como medir ?
• Métodos Empíricos
Obtemos o tempo de execução através da execução
propriamente dita do algoritmo, considerando-se
entradas diversas. (Muito dependente de máquina)
• Métodos Analíticos
Obtemos uma ordem de grandeza do tempo
execução através de expressões matemáticas que
traduzam o comportamento de um algoritmo.
Um exemplo simples
Considere o trecho de código:
prod = 0;
cont = x;
repetir os comandos
prod = prod + y;
cont = cont - 1;
ate que cont=0
Que parâmetros usar nas expressões matemáticas
que representam o custo de um algoritmo?
Usamos o tamanho da entrada,
que depende do problema.
Exemplos
Ordenação: Número de itens da entrada
(Tamanho n do vetor a ordenar).
Multiplicação de 2 inteiros: Número total de bits
necessários para representar a entrada em notação binária.
Grafos: Número de vértices e arestas do grafo.
IDÉIA CENTRAL
Tempo de execução = No. de passos efetuados pelo algoritmo
Exemplo
Algoritmo Inversão de sequência
Entrada: sequência de elementos armazenados no vetor
S[i], i = 1 .. n.
Saída: sequência invertida dos elementos de S[i].
Início
Para i := 1, ..., n/2 faça
temp := S[i]
S[i] := S[n – i + 1]
S[n – i + 1] := temp
Fim
Classificação (complexidade de tempo)
Notação:
A - um algoritmo.
E = {E1,...,Em} – conjunto de entradas possíveis de A.
ti = No. de passos efetuados por A com entrada Ei.
Definição:
Complexidade de pior caso = Max (Ei  E) {ti},
Complexidade do caso médio = Σ (1 <= i <= m)(pi * ti)
onde pi é a probabilidade de ocorrência da entrada Ei.
As Notações O, Ω e Θ
Definição (notação O) = Limite superior para o tempo de
execução.
Definição (notação Ω) = Limite inferior para o tempo de
execução.
Definição (notação Θ) = Tempo de execução exato.
Tempo de execução =
No. de passos dominantes efetuados pelo algoritmo.
Obs: Nas definições de complexidade desprezamos
as constantes aditivas ou multiplicativas.
Ex:
Número de passos = 3n  Aproximado = n
Obs: Também desprezamos os termos de menor grau.
Ex: No. de passos = n2 + n
 Aproximado = n2
No. de passos = 6n3 + 4n – 9  Aproximado = n3
Por que? Porque o interesse é assintótico.
Definição (notação O):
Sejam f,h funções positivas de variável inteira n.
Diz-se que f é O(h), escrevendo-se f = O(h),
quando existirem (1) uma constante c > 0 e
(2) um inteiro n0, tais que:
n > n0 => f(n)  c . h(n)
Ex:
f = n2 + 1
f = n2 + 1
f = 403
f = 3n + 5 log n + 2
f = 5 · 2n + 12 · 5n10





f = O(n2) (c=3, n0 = 4)
f = O(n3) (c=3, n0 = 4)
f = O(1) (c= ?, n0 = ?)
f = O(n)
f = O(2n)
Definição (notação  ):
Sejam f,h funções positivas de variável inteira n.
Diz-se que f é (h), escrevendo-se f = (h),
quando existir uma constante c > 0 e um valor
inteiro n0, tal que:
n > n0 => f(n)  c . h(n)
Ex:
 f = (n2)
f = (n)
f = (1)
Mas não vale: f = (n3)
f = n2 – 1
Definição (notação  ):
Sejam f e h funções positivas de variável inteira.
Diz-se que f é (h), escrevendo-se f = (h),
quando ambas as condições acontecem:
f = O(h) e f = (h).
Referência Bibliográfica
Introduction to Algorithms
Cormen, Leiserson, Rivest
- Capítulo 1: Introduction (págs. 1 a 11)
- Capítulo 2: Growth of Functions (págs 23 a 29)