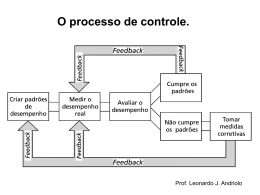
UNIVERSIDADE GAMA FILHO
PROCET – DEPARTAMENTO DE ENGENHARIA CONTROLE E
AUTOMAÇÃO
Professor Leonardo Gonsioroski
Definição
O termo “resposta em frequência” significa resposta em regime estacionário de
um sistema com entrada senoidal.
Um sistema LIT sujeito a uma entrada senoidal, produzirá em regime
estacionário uma saída senoidal com a mesma frequência da entrada, mas sua
amplitude e fase serão diferentes do sinal senoidal de entrada.
Professor Leonardo Gonsioroski
Definição
Podemos verificar essa afirmação, aplicando transformadas de Laplace.
Aplicando Frações parciais
Y s  
a
b

s  j  s  j 
Y s   Gs X s 
Então:
 A 
A  G j 
A


a  Gs  2
s

j



2




Y s   G
s
A

G
s
s  2
2j
s   2 s  j s  j s  j 
b  Gs 
 A
A  G j 


s

j


s2   2
2j
s   j
Frações Parciais – Rever Aula 3 – Transformadas
de Laplace e Equações Diferenciais
Professor Leonardo Gonsioroski
A  G  j  A  G  j 
2j
2j
Y s  

s  j 
s  j 
Fazendo: G  j   G  j   e j
G  j   G  j   e  j
A  G j   e j A  G j   e  j
2j
2j
Y s  

s  j 
s  j 
Aplicando transformada inversa teremos:
yt  
A  G j   e j
2j
 e jt 
A  G j   e j
2j
 e jt
e j t    e  j t  
yt   A  G j 
2j
yt   A  G j  sent   
Professor Leonardo Gonsioroski
Diagrama de Bode
Os Diagramas de Bode são 2 gráficos traçados em relação à frequência em
escala logarítmica:
 Um gráfico do Módulo em dB da Função de Transferência
 Um gráfico do ângulo de fase da Função de Transferência
Professor Leonardo Gonsioroski
Ganho em Decibel
Fase em Graus
Frequência em Escala Logarítimica
Professor Leonardo Gonsioroski
Diagrama de Bode
Uma Função de Transferência normalmente é composta por um ou mais dos
fatores básicos mencionados abaixo:
• Ganho K
• Fatores puramente integral e derivativo (jω)±1
• Fatores de primeira ordem (1+jωT)±1
• Fatores quadráticos [1+2ξ (jω / ωn)+(jω / ωn)2]±1
Professor Leonardo Gonsioroski
Ganho K
Quando o Ganho é um número maior que uma unidade, ele irá possuir um
valor positivo em decibéis.
Quando o Ganho for um número menor que uma unidade, ele irá possuir
um valor negativo em decibéis.
A curva de módulo em dB de um ganho constante K é uma reta horizontal
de valor 20 log K decibéis.
O ângulo de fase do ganho K é zero.
Por Exemplo: A representação em Diagramde de Bode de um Ganho K = 3
Professor Leonardo Gonsioroski
Professor Leonardo Gonsioroski
Fator Integral e Fator Derivativo
O valor do Módulo em dB do fator Integral é:
O ângulo de fase do fator integral é:
Professor Leonardo Gonsioroski
Fator Integral
Módulo do fator Integral em dB
Ângulo de fase do fator integral
Professor Leonardo Gonsioroski
Fator Derivativo
Como é de se esperar o Módulo
e a fase do fator derivativo serão:
Módulo do fator derivativo em dB
Ângulo de fase do fator derivativo
Professor Leonardo Gonsioroski
Fator de primeira ordem tipo integral
O módulo em dB para o fator de primeira ordem 1/(1+jT) é:
Professor Leonardo Gonsioroski
Fator de primeira ordem tipo integral
Analisando o módulo para o fator de primeira ordem 1/(1+jT)
temos:
Para baixas
freqüências, como
w << 1/T
Para altas
freqüências, como
w >>1/T
Professor Leonardo Gonsioroski
Fator de primeira ordem tipo integral
Professor Leonardo Gonsioroski
Fator de primeira ordem tipo integral
A fase para o fator de primeira ordem 1/(1+jT) é:
Parte Imaginária
Parte Real
Professor Leonardo Gonsioroski
Fator de primeira ordem tipo integral
A fase para o fator de primeira ordem 1/(1+jT) é:
Para a
freqüências, igua
a zero, w = 0
Para freqüência
de canto w = 1/T
Para altas
freqüências
Professor Leonardo Gonsioroski
Fator de primeira ordem tipo integral
Para a
freqüências, igua
a zero, w = 0
Para freqüência
de canto w = 1/T
Para altas
freqüências
Professor Leonardo Gonsioroski
Fator de primeira ordem tipo integral
Frequência de Corte
Professor Leonardo Gonsioroski
Vamos Relembrar …
Função de Transferência de um Filtro RC passa baixa
vin
Filtro RC
Passa Baixa
vout
Função de
Transferência do
Filtro
Professor Leonardo Gonsioroski
Vamos Relembrar …
Função de Transferência de um Filtro RC passa baixa
vin
Filtro RC
Passa Baixa
vout
Onde:
Professor Leonardo Gonsioroski
Fator de primeira ordem tipo derivativo
O módulo em dB para o fator de primeira ordem (1+jT) é:
A fase para o fator de primeira ordem 1/(1+jT) é:
Professor Leonardo Gonsioroski
Fator de primeira ordem tipo derivativo
Fazendo a mesma análise, chegamos a conclusão de que o
Diagrama de Bode será:
Professor Leonardo Gonsioroski
Funções de Transferência com Fatores de 2a. Ordem
As funções de Transferência frequentemente possuem fatores
quadráticos.
Quando os pólos de uma função de transferência de 2a. Ordem
são reais, podemos considerar que a função de transferência é
composta de dois fatores de primeira ordem.
Agora como fazer se os pólos forem complexos??
Professor Leonardo Gonsioroski
Fator quadrático do tipo integral
Professor Leonardo Gonsioroski
Fator quadrático do tipo integral
Para baixas
freqüências,
como  << n
Para altas
freqüências,
como  >>n
Professor Leonardo Gonsioroski
Fator quadrático do tipo integral
Professor Leonardo Gonsioroski
Fator quadrático do tipo integral
Professor Leonardo Gonsioroski
Fator quadrático do tipo integral
Professor Leonardo Gonsioroski
Fator quadrático do tipo integral
Professor Leonardo Gonsioroski
Fator quadrático do tipo integral
Professor Leonardo Gonsioroski
Frequência de Ressonância
g()
Professor Leonardo Gonsioroski
Frequência de Ressonância
Professor Leonardo Gonsioroski
Frequência de Ressonância
Professor Leonardo Gonsioroski
Frequência de Ressonância
Professor Leonardo Gonsioroski
Frequência de Ressonância
Professor Leonardo Gonsioroski
Procedimento Geral para Construção de um Diagrama de Bode
Revisar os diagramas de bode de todos os fatores básicos. (Escrever no
quadro)
Para escrever o diagrama de bode de uma função de transferência qualquer
temos que primeiramente expandí-la em seus fatores básicos.
Depois desenharemos os diagramas de bode de cada fator básico
separadamente
E por último realizamos a soma das contribuições de cada diagrama de
bode de cada fator básico.
Fazer Exemplo no Quadro
Professor Leonardo Gonsioroski
Determinação Experimental de Função de Transferência
de Fase Mínima.
1) O primeiro passo é traçar retas assintotas as curvas de módulo do
diagrama de bode. AS assíntotas devem ter inclinações múltiplas de + ou –
20 dB/década.
2) Nas baixas frequências a inclinação de 0 dB, -20 dB/dec ou -40 dB/dec,
indica a existência de nenhum, um ou dois pólos na origem do sistema,
respectivamente.
3) Nas altas frequências, observar as mudanças na inclinação das curvas de
módulo. Se a curva mudar em -20 dB/década é porque existe um fator de
primeira ordem na frequência em que ocorreu a mudança.
Se a mudança for de -40 dB/decada é porque existe um fator quadrático
nesta frequência.
Professor Leonardo Gonsioroski
Determinação Experimental de Função de Transferência
de Fase Mínima.
4) Os ângulos de fase nas frequências muito altas para sistemas de fase
mínima são -90º (q – p), isso nos dá uma noção da diferença do grau do
numerador para o denominador da função de transferência.
Professor Leonardo Gonsioroski
Exemplo:
Professor Leonardo Gonsioroski
Sistemas de Fase Mínima e Sistemas de Fase não Mínima
As funções de Transferência que não possuem pólos nem zeros no semiplano direito do plano complexo, são ditas de fase mínima.
As funções de transferência que possuem pólos e/ou zeros no semi plano
direito do plano complexo, são ditas de fase não mínima.
Professor Leonardo Gonsioroski
Para um sistema de fase mínima o ângulo de fase, quando a frequência
tende ao infinito, vale:
Num sistema de fase não mínima, a fase do sistema quando a frequência
tende ao infinito, difere desse valor.
Em ambos os casos a curva de módulo em dB, quando a frequencia tende
ao infinito, vale:
Professor Leonardo Gonsioroski
Margem de Fase
A Margem de fase é o atrase de fase adicional, na frequência de
cruzamento de ganho, necessária para que o sistema atinja o limiar de
instabilidade.
A frequência de cruzamento de ganho é a frequência na qual o módulo da
função de transferência de malha aberta é unitário.
A margem de fase é 180 graus mais o ângulo de fase da função de
transferência de malha aberta na frequência de cruzamento de ganho.
Para que um sistema de fase mínima seja estável a margem de fase
deve ser positiva.
Professor Leonardo Gonsioroski
Margem de Ganho
A Margem de ganho é a diferença de 0 dB e o valor do módulo, na
frequência de cruzamento de fase.
A frequência de cruzamento de fase é a frequência na qual a fase da
função de transferência de malha aberta é -180 graus.
Se a margem de ganho for positiva, o sitema será estável.
Se a margem de ganho for negativa, o sitema será instável.
Professor Leonardo Gonsioroski
Num sistema de fase não mínima, para termos estabilidade as
margens de fase e ganho devem ser negativas.
Professor Leonardo Gonsioroski
Professor Leonardo Gonsioroski