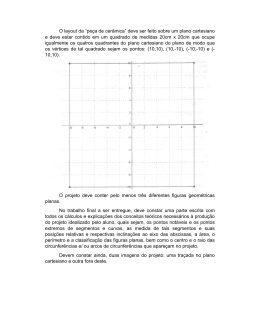
GOVERNO DO ESTADO DE SÃO PAULO
SECRETARIA DA EDUCAÇÃO
Avaliação da Aprendizagem em Processo
Comentários e Recomendações Pedagógicas
Subsídios para o Professor
1º série do Ensino Médio
Matemática
Prova 01
São Paulo, 2011
1
COORDENARIA DE ESTUDOS E NORMAS PEDAGÓGICAS
Coordenadora
Leila Aparecida Viola Mallio
Assessoria de Currículo e Avaliação
Angélica Fontoura Garcia Silva
Maria Cecília Travain Camargo
Maria Julia Filgueira Ferreira
Regina Aparecida Resek Santiago
Matemática
Coordenação e co-autoria
Juvenal de Gouveia
Sandra Maira Zen Zacarias
Vanderlei Aparecido Cornatione
Autoria
Cristina Aparecida da Silva
Edineide Santos Chinaglia
Edson Basilio Amorim Filho
João Acacio Busquini
Odete Guirro de Paula
Rosana Jorge Monteiro
Tatiane Dias Serralheiro
Revisão e Leitura Críticas
Angélica da Fontoura Garcia Silva
Ruy Cesar Pietropaolo
2
Questão 1: Disponha os seguintes números na reta numérica:
2
11
4
3,1
1
5
3
2
3
HABILIDADE: Localizar números reais na reta numérica.
Resposta correta:
Espera-se, nesta etapa de escolarização, que o aluno já tenha ampliado seus conhecimentos a
respeito dos conjuntos numéricos e identifique a localização aproximada de números reais na
reta numérica. Assim, era esperado que os alunos localizassem corretamente todos os
números que lhes foram solicitados.
No entanto, os não-acertos não significam, necessariamente, falta de domínio da habilidade
avaliada; pelo contrário, podem indicar compreensão parcial dos números reais, certamente
ainda em construção pelos alunos.
Neste sentido, é importante a identificação dos conhecimentos de cada aluno com relação à
localização de números reais. A grade a seguir pode auxiliar o professor nessa tarefa.
Indique o que você conclui a respeito dos conhecimentos do aluno relacionados à localização
de números reais a partir dos registros por ele apresentados.
Categorias para análise
Sim/Não
O aluno localiza corretamente todos os números reais solicitados.
O aluno localiza corretamente apenas os números positivos.
O aluno localiza corretamente apenas os números negativos.
2.
11
O aluno localiza corretamente apenas o número
.
4
1
O aluno localiza corretamente apenas o número
.
5
O aluno localiza corretamente apenas o número
O aluno localiza corretamente apenas o número 3,1.
O aluno localiza corretamente apenas o número
3
.
2
O aluno troca a posição dos números negativos (troca a posição do
4
número
1
com a do número
5
3
).
2
O aluno demonstra total falta de domínio da habilidade avaliada.
O aluno deixou em branco a questão.
Algumas referências:
O estudo da temática em questão pode ser complementado ou retomado observando
as propostas apresentadas nos seguintes materiais:
1-Caderno do Professor: Matemática – Ensino Fundamental – 8ª série/9º ano –
Volume 1
Situação de Aprendizagem 1 – Conjuntos e números (p. 10).
Situação de Aprendizagem 3 – Aritmética, álgebra e geometria com a Reta Real (p. 31).
2-Caderno do Professor: Matemática – Ensino Fundamental – 8ª série/9º ano –
Volume 4
Situação de Aprendizagem 1 – A natureza do número Pi (π) (p. 11).
1- Material de apoio para a Recuperação:
+ MATEMÁTICA – Coletânea de Atividades – Volume 3
Atividade 3 – Representação e ordenação
Atividade 4 – Oposição e simplificação
Atividade 6 – Números racionais
5
Questão 2: SAEB (2009) Os vértices do triângulo representado no plano cartesiano a seguir são
(A) K (5,-2); L (1,-3) e M (4,3).
(B) K (2,-5); L (-3,-1) e M (3,-4).
(C) K (-2,5); L (-3,1) e M (3,4).
(D) K (-3,0); L (-2,0) e M (3,0).
HABILIDADE: identificar as coordenadas de pontos no plano cartesiano.
ALTERNATIVAS
(A) K (5,-2); L (1,-3) e M (4,3).
JUSTIFICATIVAS
Resposta errada, o aluno não identifica
corretamente as coordenadas no plano
cartesiano (vértices do triângulo), pois
troca a ordem: no par, em vez de
indicar primeiro a abscissa e depois a
ordenada, faz justamente o contrário.
(B) K (2,-5); L (-3,-1) e M (3,-4).
Resposta errada, o aluno não identifica
corretamente as coordenadas dos
vértices do triângulo no plano
cartesiano,
pois
não
identifica
corretamente os números que indicam
as coordenadas.
(C) K (-2,5); L (-3,1) e M (3,4).
Resposta correta, o aluno identifica
corretamente as coordenadas dos
vértices do triângulo no plano
6
cartesiano.
(D) K (-3,0); L (-2,0) e M (3,0).
Resposta errada, o aluno não identifica
corretamente as coordenadas no plano
cartesiano dos vértices do triângulo,
pois indica a projeção dos vértices no
eixo das abscissas.
Para desenvolver esta habilidade – identificar as coordenadas de um ponto no plano
cartesiano – os alunos precisam reconhecer a convenção: utiliza-se um par ordenado em que o
primeiro elemento do par indica a distância do ponto ao eixo-y e o segundo a distância ao
eixo-x.
O professor pode propor aos alunos atividades lúdicas que podem favorecer a
compreensão da necessidade de haver dois eixos para localizar um ponto ou uma região no
plano. O jogo de batalha naval é um exemplo desse tipo de atividade, auxilia na compreensão
de informações que determinam regiões no plano cartesiano. Todavia, é fundamental assinalar
a diferença entre o sistema de eixos cartesianos do sistema utilizado na batalha naval: no
plano cartesiano as coordenadas indicam pontos ao passo que na batalha naval indicam
regiões. Além disso, para não confundir, na batalha utiliza-se letras para um dos eixos e
números para o outro; assim a questão da ordem fica minimizada. As mesmas considerações
devem ser observadas para os Guias de Ruas das cidades ou bairros, pois as coordenadas são
representadas por letras e números, referentes à informação horizontal e à vertical.
ALGUMAS REFERÊNCIAS:
1-Caderno do Professor: Matemática – Ensino Fundamental - 7ª série/ 8º ano – Volume 3
Situação de Aprendizagem 2 – Coordenadas cartesianas e transformações no
plano (p.25-37).
2-Experiências Matemáticas – 7ª série
Atividade 7 – Coordenadas Cartesianas (p.85-94).
3 - + Matemática – Volume 3
Atividade 17 – Coordenadas Cartesianas (Caderno do Professor – p.62)
4 – Telecurso 2000 - Aula 66 – Plano Cartesiano
http://www.youtube.com/watch?v=pKxW_8deak4
Acesso em 21-07-2011
7
5-Revista Nova Escola - Localização de um ponto no plano
Objetivo: Identificar a localização de objetos numa malha quadriculada, coordenando as
informações de dois eixos (linhas e colunas) para determinar a localização de um ponto.
http://revistaescola.abril.com.br/matematica/pratica-pedagogica/localizacao-ponto-plano511493.shtml
Acesso em 21-07-2011
8
Questão 3: Um depósito, contendo inicialmente 800 litros de água, dispõe de uma válvula na
sua parte inferior. Um dispositivo registrou a quantidade de água a cada instante a partir do
momento em que a válvula foi aberta (t = 0). Os dados obtidos permitiram construir o gráfico
da quantidade V (em litros) em função do tempo t (em minutos).
Pode-se afirmar que durante o intervalo de
(A) 0 a 10 min o depósito perdeu 500 litros.
(B) 10 min a 35 min, o depósito perdeu 300 litros.
(C) 10 min a 35 min, o depósito perdeu 500 litros.
(D) 0 a 60 min, o depósito perdeu 800 litros.
HABILIDADE: Ler e interpretar um gráfico cartesiano que indica a variação de duas
grandezas.
ALTERNATIVAS
(A) 0 a 10 min o depósito perdeu 500 litros.
(B) 10 min a 35 min, o depósito perdeu 300
litros.
JUSTIFICATIVAS
Resposta errada. O aluno não analisa
adequadamente o gráfico e retira informação
incorreta lendo no eixo y somente a indicação
correspondente a 10 minutos.
Resposta errada. Possivelmente ao analisar o
gráfico, o aluno não percebe que neste
período de tempo não há perda de água, o
que é indicado pela função constante.
(C) 10 min a 35 min, o depósito perdeu 500 Resposta errada. Possivelmente o aluno
9
analisa o gráfico e não identifica
corretamente o que a função constante
indica, no caso não houve vazão.
litros.
(D) 0 a 60 min, o depósito perdeu 800 litros.
Resposta
correta.
O
aluno
resolve
corretamente. Analisa o gráfico e extrai as
informações necessárias para a solução do
problema.
Algumas referências:
1 - Caderno do Professor: Matemática – Ensino Fundamental - 1ª série Ensino Médio –
Volume 2
Situação de Aprendizagem 2 – Funções do 1º grau: significado, gráficos,
crescimento, decrescimento, taxas. (p.20).
2 - Nova Escola
http://revistaescola.abril.com.br/matematica/pratica-pedagogica/conceito-grafico-funcaoafim-629412.shtml
Acesso em 21-07-2011
http://revistaescola.abril.com.br/matematica/pratica-pedagogica/funcao-afim-resolucaoproblemas-626737.shtml
Acesso em 21-07-2011
10
Questão 4: O segmento AB representado no sistema de eixos cartesianos é um dos lados de
um quadrado situado no primeiro quadrante.
Represente o quadrado na malha quadriculada acima e indique as coordenadas dos seus
vértices.
HABILIDADE: Construir um quadrado no plano cartesiano, identificando as coordenadas de
seus vértices.
Alguns procedimentos corretos para resolver o problema:
O aluno representa corretamente o quadrado solicitado.
C
D
O aluno que faz essa representação, provavelmente reconhece ou identifica:
propriedades do quadrado;
a ideia da distância entre dois pontos;
o conceito de localização de pontos no plano cartesiano.
11
Categorias para análise
Sim/Não
O aluno constrói corretamente um quadrado no plano cartesiano e
identifica seus vértices (par ordenado).
O aluno constrói corretamente um quadrado no plano cartesiano e
não identifica os vértices do quadrado (par ordenado).
O aluno constrói um quadrado usando o segmento AB como lado
superior.
O aluno constrói um quadrado usando o segmento AB como lado
superior.
O aluno não constrói um quadrado no plano cartesiano, pois não
domina as propriedades do quadrado, mas indica algum grau de
conhecimento desse plano, indicando, por exemplo, as coordenadas
dos dois vértices dados.
O aluno não constrói um quadrado no plano cartesiano, pois não
domina as propriedades do quadrado e não identifica corretamente
os vértices da figura construída, demonstrando total falta de domínio
da habilidade avaliada.
O aluno deixa a questão em branco.
ALGUMAS REFERÊNCIAS:
1-Caderno do Professor: Matemática – Ensino Fundamental - 7ª série/ 8º ano – Volume 3
Situação de Aprendizagem 2 – Coordenadas cartesianas e transformações no
plano (p.25-37).
2-Experiências Matemáticas – 7ª série
Atividade 7 – Coordenadas Cartesianas (p.85-94).
3 - + Matemática – Volume 3
Atividade 17 – Coordenadas Cartesianas (Caderno do Professor – p.62)
12
Questão 5: Considere a representação algébrica da função polinomial do 1º grau y
Construa o gráfico que a representa.
x
2.
HABILIDADE: Construir gráficos de uma função polinomial do 1º grau.
Alguns procedimentos corretos para resolver o problema:
O aluno que representou corretamente obteve o seguinte gráfico:
Indique, a seguir, o que você conclui a respeito do apresentado pelo aluno.
13
Categorias para análise
O aluno indica e traça corretamente a linha da função afim.
O aluno indica os pontos, mas não traça a linha referente à
função.
O aluno desenha uma reta crescente qualquer diferente da
correta, mas mostra que reconhece que uma função polinomial
do 1º grau é uma reta e que essa reta é crescente tendo em
vista que o coeficiente angular é positivo.
O aluno desenha uma reta decrescente ou horizontal, mas não
desenha os eixos do plano, mostrando apenas que reconhece
que uma função polinomial do 1º grau é representada no plano
por meio de uma reta.
O aluno troca as abscissas pelas ordenadas.
O aluno constrói uma curva qualquer.
O aluno demonstra total falta de domínio da habilidade avaliada.
O aluno deixa a questão em branco.
Sim/Não
ALGUMAS REFERÊNCIAS:
1-Caderno do Professor: Matemática – Ensino Fundamental - 7ª série/ 8º ano – Volume 3
Situação de Aprendizagem 2 – Coordenadas cartesianas e transformações no
plano (p.25-37).
2-Experiências Matemáticas – 7ª série
Atividade 7 – Coordenadas Cartesianas (p.85-94).
3 - + Matemática – Volume 3
Atividade 17 – Coordenadas Cartesianas (Caderno do Professor – p.62)
4 – Telecurso 2000 - Aula 66 – Plano Cartesiano
http://www.youtube.com/watch?v=pKxW_8deak4
Acesso em 21-07-2011
5-Revista Nova Escola - Localização de um ponto no plano
http://revistaescola.abril.com.br/matematica/pratica-pedagogica/localizacao-ponto-plano511493.shtml
Acesso em 21-07-2011
Nova escola
14
http://revistaescola.abril.com.br/matematica/pratica-pedagogica/conceito-grafico-funcaoafim-629412.shtml
Acesso em 21-07-2011
http://revistaescola.abril.com.br/matematica/pratica-pedagogica/funcao-afim-resolucaoproblemas-626737.shtml
Acesso em 21-07-2011
15
Questão 6: O gráfico a seguir representa uma função polinomial do 2º grau.
A representação algébrica da função que corresponde ao gráfico é
(A) f(x) = x² + 2.
(B) f(x) = x² - 2.
(C) f(x) = -x² + 2.
(D) f(x) = -x² - 2.
HABILIDADE: identificar a representação algébrica de uma função polinomial do 2º grau a
partir de sua representação gráfica.
ALTERNATIVAS
(A) f(x) = x² + 2.
(B) f(x) = x² - 2.
JUSTIFICATIVAS
Resposta errada, pois o aluno provavelmente
identifica corretamente que o valor positivo
do coeficiente a define a concavidade da
parábola para cima, mas não identifica
corretamente o ponto de intersecção da
parábola com o eixo y.
Resposta correta, pois o aluno provavelmente
identifica corretamente que o valor positivo
do coeficiente a define a concavidade da
parábola para cima e que o coeficiente c da
função determina a intersecção da parábola
com o eixo y.
16
(C) f(x) = -x² + 2.
Resposta errada, pois o aluno provavelmente
não identifica que o valor negativo do
coeficiente a definiria a concavidade da
parábola para baixo e não identifica
corretamente o ponto de intersecção da
parábola com o eixo y.
(D) f(x) = -x² - 2.
Resposta errada, pois o aluno provavelmente
identifica que o coeficiente c da função
determina a intersecção da parábola com o
eixo y, mas não identifica que o valor negativo
do coeficiente a definiria a concavidade da
parábola para baixo.
Algumas referências:
O desenvolvimento deste tema esta proposto para a 1ª série em:
Caderno do Professor: Matemática – Ensino Médio 1ª série – volume 2
Situação de Aprendizagem 3 – Funções de 2º grau: significado, gráficos, intersecções com
os eixos, vértices, sinais
O estudo da temática em questão pode ser complementado observando também as
propostas apresentadas nos seguintes materiais:
1- Material de apoio para Recuperação:
+ MATEMÁTICA – 2ª SÉRIE – ENSINO MÉDIO
Aula 12 – Identificando gráficos de funções quadráticas
Aula 13 – Identificar uma função quadrática a partir de seu gráfico
Aula 14 – Simetria da parábola
2- Softwares:
Janelas em arco e ferradura
http://m3.ime.unicamp.br/portal/Midias/Softwares/SoftwaresM3Matematica/arc
o_ferradura/ferradura/visualizar.html
Acesso em 21-07-2011
Janelas em arco romano
17
http://m3.ime.unicamp.br/portal/Midias/Softwares/SoftwaresM3Matematica/
arco_romano/arco_romano/visualizar.html
Acesso em 21-07-2011
Winplot:
http://math.exeter.edu/rparris/winplot.html
Acesso em 21-07-2011
Geogebra
http://www.geogebra.org/cms/
Acesso em 21-07-2011
Experimento
http://m3.ime.unicamp.br/portal/Midias/Experimentos/ExperimentosM3Matematica/otimiza
cao_da_cerca/
Acesso em 21-07-2011
18
Questão 7: Saeb (2009) Hélio e Ana partiram da casa dela com destino à escola. Ele foi direto
de casa para a escola e ela passou pelo correio e depois seguiu para a escola, como mostra a
figura a seguir:
De acordo com os dados apresentados, a distância percorrida por Ana foi maior que a
percorrida por Hélio em
(A) 200 m.
(B) 400 m.
(C) 800 m.
(D) 1 400 m.
HABILIDADE: Resolver problemas em diferentes contextos que envolvam as relações métricas
dos triângulos retângulos (Teorema de Pitágoras).
ALTERNATIVAS
(A) 200 m.
(B) 400 m.
JUSTIFICATIVAS
Resposta errada, o aluno provavelmente efetuou a
subtração (800 – 600) ignorando a distância
percorrida por Hélio.
Resposta correta, o aluno provavelmente fez os
cálculos utilizando o Teorema de Pitágoras, para
descobrir a distância percorrida por Hélio. Em
seguida calculou a distância percorrida por Ana e
finalmente a diferença entre Hélio e Ana.
Distância percorrida por Hélio:
19
h2
a2 b2
h2
600 2 800 2
h
1000000
360000
640000
1000000
1000 m
Distância percorrida por Ana: 600 + 800 = 1400m
A diferença:
d=1400 – 1000 = 400 m
(C) 800 m.
Resposta errada, o aluno provavelmente considera
somente a distância do correio à escola percorrida
por Ana.
(D) 1 400 m.
Resposta errada, o aluno provavelmente interpreta
incorretamente a comanda e considera apenas a
distância percorrida por Ana ignorando a distância
percorrida por Hélio.
ALGUMAS REFERÊNCIAS:
1-Caderno do Professor: Matemática – Ensino Fundamental - 8ª série/ 9º ano – Volume 3
Situação de Aprendizagem 3 – Relações métricas nos triângulos Retângulos:
Teorema de Pitágoras (p.30 - 41).
Novo Telecurso - Ensino Médio - Matemática - Teorema de Pitagoras
http://www.youtube.com/watch?v=ZkESIB7IjNw
Acesso em 21-07-2011
Novo Telecurso - Ensino Médio - Matemática - Aula 19 (1 de 2 e 2 de 2)
http://www.youtube.com/watch?v=zsj8jcRhQWk
Acesso em 21-07-2011
Software – Tem TOP10
Este módulo utiliza tecnologia 3D para uma melhor aprendizagem do Teorema de Pitágoras.
Existem 3 versões que se distinguem apenas pela qualidade da imagem e animação:
http://nautilus.fis.uc.pt/mn/pitagoras/pitflash1.html Acesso em 21-07-2011
20
Questão 8: Observe o retângulo
(x-2) cm
(x + 3) cm
Área do retângulo: 36 cm2.
Expresse a equação que relaciona as medidas dos lados do retângulo à sua área.
HABILIDADE: Expressar problemas por meio de equações.
Alguns procedimentos corretos para resolver o problema:
1. O aluno indica corretamente a equação 2. O aluno indica a equação correspondente
correspondente ao problema proposto,
e desenvolve corretamente a sentença.
mas não efetua nem simplifica a
(x – 2 ) . (x + 3) = 36
sentença (não lhe foi solicitado os
x2 + 3x – 2x – 6 = 36
cálculos).
x2 + x = 42
(x – 2 ) . (x + 3) = 36
ou
x2 = 42 – x
ou
x2 + x – 42 = 0
Indique, a seguir, o que você conclui a respeito do apresentado pelo aluno.
Categorias para análise
O aluno escreve corretamente a equação correspondente ao
problema proposto escrevendo-a da forma ax 2
bx c
Sim/Não
0
O aluno escreve corretamente a equação correspondente ao
problema
ax 2
proposto,
bx c
mas
não
a
escreve
da
forma
0 , pois não lhe foi solicitado que efetuasse o
produto das expressões algébricas.
O aluno indica corretamente a equação correspondente e
21
procura efetuar o produto e simplificações, mas não o faz
adequadamente.
O aluno indica uma outra equação e desenvolve corretamente a
sentença.
O aluno demonstra total falta de domínio da habilidade avaliada.
O aluno deixou em branco a questão.
Algumas referências:
Caderno do professor – 8ª série/ 9º ano – Volume 2
Situação de Aprendizagem1: Alguns métodos para resolver equações de 2º grau
(p. 12-19).
22
Questão 9: Saeb (2009) As variáveis n e p assumem valores conforme mostra a figura
abaixo.
A relação entre p e n é dada pela expressão
(A) p = n + 1.
(B) p = n + 2.
(C) p = 2n – 2.
(D) p = n – 2.
HABILIDADE: Identificar a expressão algébrica que expressa uma regularidade observada em
sequência de números ou figuras (padrões).
ALTERNATIVAS
(A) p = n + 1.
JUSTIFICATIVAS
Resposta errada, provavelmente o
aluno não faz a relação entre as
variáveis, ignorando a segunda linha da
tabela (p) e analisando somente a
sequência da primeira linha (n).
(B) p = n + 2.
Resposta errada, provavelmente o
aluno não faz a relação entre as
variáveis, ignorando a primeira linha da
tabela (n) e analisando somente a
sequência da segunda linha (p).
(C) p = 2n – 2.
Resposta correta, o aluno identifica
corretamente a expressão algébrica
que expressa a regularidade observada
na sequência de números.
(D) p = n – 2.
Resposta
errada,
o
aluno
provavelmente não faz a relação entre
as variáveis, ignorando a primeira linha
da tabela (n) e analisa, da direita para a
esquerda, somente a sequência da
23
segunda linha (p).
ALGUMAS REFERÊNCIAS:
O desenvolvimento deste tema está proposto para o 1ª série do E.M. em:
1-Caderno do Professor: Matemática – Ensino Fundamental -1ª série – Volume 1
Situação de Aprendizagem 1 – Conjuntos Numéricos; Regularidades Numéricas
e/ou Geométricas (p. 11-22).
O estudo da temática em questão pode ser complementada observando também as
propostas apresentadas nos seguintes materiais:
1-Caderno do Professor: Matemática – Ensino Fundamental - 7ª série/ 8º ano – Volume 2
Situação de Aprendizagem 1 – Aritmética com Álgebra: as letras como
números (p. 11-19).
2 - + Matemática – Coletânea de Atividades - Volume 3
Atividade 7 – Generalizações (Caderno do Professor – p.23)
Atividade 8 – Relações (Caderno do Professor – p.25)
Atividade 9 – Propriedades ( Caderno do Professor – p. 28)
24
Questão 10: O custo C de produção, em milhares de reais, de x máquinas iguais é dado pela
expressão C(x) = x2 – x + 10. Sabendo que o custo foi de 52 mil reais, qual o número de
máquinas produzidas?
HABILIDADE: Resolver problema que envolva equação do 2º grau.
Alguns procedimentos corretos para resolver o problema :
1. O aluno resolve a equação x² - x + 10 =
2. O aluno resolve a equação x² - x + 10 =
52 por meio do método de completar
52 por meio da fórmula de Bhaskara:
quadrados.
x
x
x
b
b ² 4ac
2a
( 1)
( 1)² 4(1)( 42 )
2(1)
1 13
x' 7 ou x'' -6
2
Logo, o número de máquinas produzidas é 7.
x²
x 10 52
x²
x
x
1
2
x
1
2
42
2
42
2
1
4
169
4
x' 7 ou x' '
6
Logo, o número de máquinas produzidas é 7.
Indique, a seguir, o que você conclui a respeito do apresentado pelo aluno.
Categorias para análise
Sim/Não
O aluno resolve corretamente a equação x² - x + 10 = 52 obtendo
como raízes -6 e 7. Considera apenas a solução 7 como resposta do
problema.
O aluno resolve corretamente a equação x² - x + 10 = 52 obtendo
como raízes -6 e 7, mas considera as duas raízes como solução do
problema, pois não apresenta a resposta final ou considera as duas
soluções em sua resposta.
O aluno não considera corretamente as informações do enunciado
do problema e resolve a equação x² - x + 10 = 0.
O aluno resolve corretamente a equação x² - x + 10 = 52 000,
esquecendo que C(x) é dado em milhares de reais.
O aluno procura resolver a equação x² - x + 10 = 52 000, mas não o
25
faz corretamente.
O aluno considera a equação correta, mas erra na resolução.
O aluno demonstra total falta de domínio da habilidade avaliada.
O aluno deixou a questão em branco.
Algumas referências:
O estudo da temática em questão pode ser complementada observando as propostas
apresentadas nos seguintes materiais:
2- Caderno do Professor: Matemática – Ensino Fundamental – 8ª série/9º ano –
Volume 2
Situação de Aprendizagem 1 – Alguns métodos para resolver equações de 2º grau.
Situação de Aprendizagem 2 – Equações de 2º grau na resolução de problemas.
3- Material de apoio para a Recuperação:
+ MATEMÁTICA – 1ª série – Ensino Médio
Aula 7 – Alguns métodos para resolver equações de 2º grau
Aula 8 – Resolvendo equações de 2º grau
Aula 9 – Equações de 2º grau na resolução de problemas
Aula 10 – Mais problemas com equações de 2º grau
26
Referências Bibliográficas
São Paulo, Secretaria de Estado da Educação. Ensinar matemática nas séries iniciais (PEC
Formação Universitária). São Paulo: SEE/CENP, Tema 5, Módulo 2, 2006.
––––––.+ Matemática: material do aluno; coletânea de atividades/Secretaria da Educação;
coordenação geral, Maria Inês Fini; equipe, Angélica Fontoura Garcia Silva, Maria Silvia
Sentelhas, Patrícia de Barros de Monteiro, Ruy César Pietropaolo, São Paulo: SEE, 2009.
––––––.+ Matemática: material do aluno; coletânea de atividades/Secretaria da Educação;
coordenação geral, Maria Inês Fini; equipe, Angélica Fontoura Garcia Silva, Maria Silvia
Sentelhas, Patrícia de Barros de Monteiro, Ruy César Pietropaolo, São Paulo: SEE, 2009.
––––––. Ler e Escrever: guia de planejamento e orientações didáticas; professor - 4 ª
Série/Secretaria da Educação, Fundação para o Desenvolvimento da Educação; adaptação do
––––––. Caderno do professor: matemática, Ensino Fundamental – 1.ª série, Volume 1, 2,4.
Coordenação Maria Inês Fini; equipe Nilson José Machado, Carlos Eduardo de Souza Granja,
José Luiz Pastore Mello, Walter Spinelli, Rogério Ferreira da Fonseca, Ruy César Pietropaolo.
São Paulo: SEE, 2009.
––––––. Caderno do professor: matemática, Ensino Fundamental – 7.ª série, Volume 2e 3.
Coordenação Maria Inês Fini; equipe Nilson José Machado, Carlos Eduardo de Souza Granja,
José Luiz Pastore Mello, Walter Spinelli, Rogério Ferreira da Fonseca, Ruy César Pietropaolo.
São Paulo: SEE, 2009.
––––––. Caderno do professor: matemática, Ensino Fundamental – 8.ª série, Volume 1, 2, 3 e
4. Coordenação Maria Inês Fini; equipe Nilson José Machado, Carlos Eduardo de Souza Granja,
José Luiz Pastore Mello, Walter Spinelli, Rogério Ferreira da Fonseca, Ruy César Pietropaolo.
São Paulo: SEE, 2009.
. São Paulo: SEE, 2009.
______. Currículo do Estado de São Paulo: Matemática e suas tecnologias. Coordenação de
Maria Inês Fini; coordenação de área, Nilson José Machado. São Paulo: SEE, 2010.
27