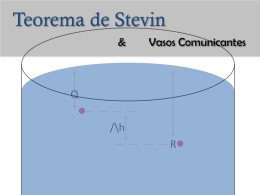
HIDROSTÁTICA
 Massa específica ou densidade absoluta. É a razão
entre a massa de uma substância pelo seu volume.
Ex: 1g/cm3 de água = 1000 Kg/m3.
- Densidade de um corpo: é a razão da massa do
corpo pelo seu volume.
m

V
HIDROSTÁTICA
 Peso Específico: Chamamos de peso
específico de um corpo à razão entre o so e o
seu volume.
 UNIDADES Sistema M.K.S : N/m3
HIDROSTÁTICA
 Pressão: Pressão de uma força sobre uma
superfície é a razão entre o módulo da força
e a área da superfície considerada.
 UNIDADES SistemaM.K.S: N/m2
 Outra unidade muito usada é a atmosfera
(atm) 1 atmosfera == 1,0 X 105 N/m2
F
p
A
HIDROSTÁTICA
 MEDIDA DA PRESSÃO HIDROSTÁTICA
 Para um líquido em repouso a pressão hidrostática depende
da massa específica, aceleração da gravidade e da
profundidade h.
 Todos os pontos da superfície que se encontram no mesmo
nível suportam a mesma pressão.
 A pressão p sobre os pontos de uma supefície é devido ao
peso P da coluna fluido sobre a superfície.
pH  .g.h
 A pressão total em um ponto, a uma profundidade h de um
líquido em equilíbrio, é a resultante da soma da pressão
atmosférica na superfície mais a pressão hidrostática.
 Pa
HIDROSTÁTICA
 TEOREMA FUNDAMENTAL DA HIDROST Á TICA
OU TEOREMA DE STEVIN
A diferença de pressão entre dois pontos quaisquer de
um líquido em equilíbrio é dada pelo produto do
desnível entre esses pontos pelo peso específico do
líquido.
PARADOXO HIDROST Á TICO
 A força que um líquido exerce sobre o fundo de um
recipiente não depende de sua forma, mas da altura do
líquido e da área da base.
EXERCÍCIO
 Três recipientes com alturas iguais a 0,5m, mas com
formatos diferentes, são totalmente preenchidos com
um mesmo líquido de densidade 103kg/m3, como
indica a figura. A área do fundo dos recipientes é 0,4m2
para todos eles. Sendo a aceleração da gravidade
10m/s2 e a pressão atmosférica igual a 105N/m2,
determine:
a) a pressão total exercida no fundo dos três recipientes;
b) a intensidade da força que atua no fundo dos três
recipientes.
HIDROSTÁTICA
EQUILÍBRIO DE UM LÍQUIDO EM VASOS
COMUNICANTES
 A altura alcançada por um líquido em equilíbrio em
diversos vasos comunicantes é a mesma, qualquer que seja
a forma ou secção dos ramos (desde que não sejam
capilares).
EQUILÍBRIO DE DOIS LÍQUIDOS IMISOÍVEIS EM VASOS
COMUNICANTES
 Dois líquidos imiscíveis em equilíbrio em vasos
comunicantes atingem alturas inversamente proporcionais
as suas massas específicas.
 1.h1  2 .h2 
EXERCÍCIO
 Água e óleo de densidades 1g/cm3 e 0,8g/cm3,
respectivamente, são colocados em um sistema de
vasos comunicantes. Sendo 26cm a altura da coluna de
óleo, acima do equilíbrio, determine a altura da coluna
de água medida acima do nível de separação entre os
líquidos.
HIDROSTÁTICA
TEOREMA DE PASCAL
 Os líquidos transmitem integralmente, em todas as
direções e sentidos, as pressões que suportam.
PRENSA HIDRÁULICA
 Uma prensa hidráulica é um sistema constituído por
dois vasos comunicantes e de diâmetros diferentes. No
interior dos vasos existe um líquido que sustenta dois
êmbolos, conforme a figura.
F1 F2

A1 A2
HIDROSTÁTICA
TEOREMA DE ARQUIMEDES
 Todo corpo mergulhado em um líquido fica submetido
à ação de uma força vertical, orientada de baixo para
cima, de valor igual ao peso do líquido deslocado, que
denominamos empuxo.
 O empuxo é igual ao peso do volume de líquido
deslocado.
 Importante:
E  .Vd .g
E = P – o corpo flutua.
E > P – o corpo sobe.
E < P – o corpo afunda.
EXERCÍCIO
 Assinale as afirmativas corretas e some seus respectivos
valores:
01- Os freios hidráulicos dos veículos automotores
constituem-se na aplicação prática do Princípio de Pascal.
02- Para que um corpo flutue é necessário que a sua massa
específica seja superior à massa específica do líquido em
que está imerso.
04- A pressão num líquido em repouso aumenta à medida
que aumenta a profundidade.
08- Um submarino completamente submerso, para emergir,
diminui o empuxo exercido sobre ele.
EXERCÍCIO
 Um balão de hidrogênio de peso igual a 600N está
preso a um fio em equilíbrio estático vertical. Seu
volume é igual a 80m3. Adote g=10m/s2. Densidade do
ar = 1,25kg/m3. Determine:
a) o empuxo exercido pelo ar sobre o balão.
b) a tração no fio que sustém o balão.
EXERCÍCIO
 Pescando no ri Tietê, na cidade de São Paulo, um turista
fisgou um pneu de massa 10,5kg, cuja densidade é de
1400kg/m3. Considerando a tabela abaixo (que fornece a
tração que uma linha de pesca pode suportar em função do
seu diâmetro), determine:
a) o diâmetro mínimo da linha de pesca, dentre os
apresentados na tabela, para que o pescador levante o
pneu, enquanto este estiver totalmente submerso;
b) o diâmetro mínimo da linha de pesca, dentre os
apresentados na tabela, para que o pescador levante o pneu
totalmente fora da água. Admita que a parte côncava
inferior do pneu retém 3 litros de água.
EXERCÍCIO
 Ao se usar um saca-rolhas, a força mínima que deve ser
aplicada para que a rolha de uma garrafa comece a sair é
igual a 360N.
a) Sendo o coeficiente de atrito estático entre a rolha e o
bocal da garrafa, encontre a força normal que a rolha exerce
no bocal da garrafa. Despreze o peso da rolha.
b) Calcule a pressão da rolha sobre o bocal da garrafa.
Considere o raio interno do bocal da garrafa igual a 0,75 cm
e o comprimento da rolha igual a 4,0 cm.
.