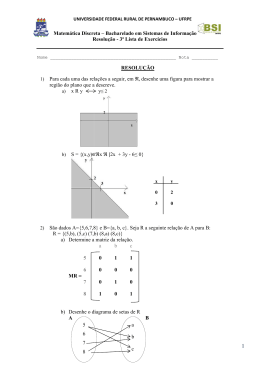
Fundamentos de Álgebra Moderna
Profª Ana Paula
CONJUNTO DOS NÚMEROS INTEIROS
Os números inteiros formam um conjunto, que notaremos por ℤ, no qual estão
definidas duas operações, que chamaremos de adição e multiplicação e denotaremos
por + e ⋅.
Notação:
ℤ = 0, ±1, ±2, ±3, …  = conjunto dos números inteiros
ℤ ∗ = ±1, ±2, ±3, …  = … , −3, −2, −1, 1, 2, 3, …  = ℤ − 0
ℤ + = 0, 1, 2, 3, …  = conjunto dos números inteiros não-negativos.
ℤ − = … , −3, −2, −1, 0 = conjunto dos números inteiros não-positivos.
ℤ ∗+ = 1, 2, 3, …  = conjunto dos números inteiros positivos ou estritamente
positivos.
ℤ ∗− = … , −3, −2, −1 = conjunto dos números inteiros negativos ou estritamente
negativos.
ℤ 2n = k ∈ ℤ/k = 2n, n ∈ ℤ =conjunto dos inteiros pares.
ℤ 2n+1 = k ∈ ℤ/k = 2n + 1 ou k = 2n − 1, n ∈ ℤ =conjunto dos inteiros ímpares.
Os axiomas que passaremos a detalhar descreverão algumas das propriedades
básicas das operações, que tomaremos como base para desenvolver a teoria. Qualquer
outra propriedade, mesmo que intuitivamente óbvia, poderá ser demonstrada a partir
dessas.
O primeiro grupo de axiomas descreverá algumas propriedades da adição:
Propriedades da adição:
A.1 Associativa: Para toda a terna a, b, c de inteiros tem-se que:
a + b + c = a + b + c.
A.2 Existência de Neutro: Existe um único elemento, denominado neutro aditivo ou
zero, que indicaremos por 0, tal que a + 0 = 0 + a = a, para todo α ∈ ℤ.
A.3 Existência de Oposto: Para cada inteiro a existe um único elemento que
chamaremos oposto de a e indicaremos por −a, tal que a + −a = 0.
A.4 Comutativa:Para todo par a, b de inteiros tem-se que a + b = b + a.
1
O outro grupo de axiomas explicita algumas das propriedades da multiplicação:
Propriedades da multiplicação:
A.5 Associativa: Para toda a terna a, b, c de inteiros tem-se que: abc = abc.
A.6 Existência de Neutro: Existe um único elemento, diferente de zero,
denominado neutro multiplicativo , que indicaremos por 1, tal que a. 1 = 1. a = a, para
todo a ∈ ℤ.
A.7 Lei do cancelamento: Para toda a terna a, b, c de inteiros, com a ≠ 0, tem-se
que, se ab = ac, então a = b.
A.8 Comutativa:Para todo par a, b de inteiros tem-se que ab = bc.
Definição: Sejam a, b ∈ ℤ. Definimos a − b = a + −b.
Proposição 1 (Propriedade cancelativa da adição): Para toda a terna a, b, c de
inteiros tem-se que, se a + b = a + c, então b = c.
Propriedade 2: :Para toda a terna a, b, c de inteiros, com a ≠ 0, tem-se que,
ab + c = ab + ac.
Proposição 3: Para todo inteiro a, tem-se que a. 0 = 0.
Proposição 4: Sejam a, b inteiros, tais que a. b = 0. Então, a = 0 ou b = 0.
Proposição 5 (Regra dos Sinais):
Sejam a, b inteiros. Então vale:
i) −−a = a
ii) −ab = −ab = a−b.
iii) −a−b = ab
Definição 1: O valor absoluto, |a|, de um número inteiro a é definido por:
|a| =
Logo, |a| ∈ ℤ + .
2
a se a ≥ 0
−a
se a < 0
Definição 2: Seja a ∈ ℤ. Definem-se
1. a = a
a0 = 1
k + 1. a = k. a + a
a k+1 = a k . a
sempre que ka e a k , para k ∈ ℤ + , estão definidas.
Propriedades: Sejam a, b ∈ ℤ e quaisquer m, n ∈ ℤ + :
1) ma + na = m + na
2) mna = m. na
3) a m . a n = a m+n
4) a n  m = a n.m
5) na + nb = na + b
6) a n . b n = ab n
Definição 3: Dados dois conjuntos, A e B, não vazios. O produto cartesiano de A
por B é o conjunto formado por todos os pares ordenados x, y, com x ∈ A e y ∈ B.
A × B = x, y/x ∈ A e y ∈ B
Exemplo: Sejam os conjuntos A = 0, 1, 2, 3 e B = 4, 5, 6. O produto cartesiano de
de A por B é dado por E × F =
Definição 4: Uma relação R é um conjunto de pares ordenados, isto é,
R = ∀a, b ∈ A × B/pa, b
Se a propriedade pa, b é verdadeira, então dizemos que "a está relacionado com b
mediante a R", aRb.
Se a propriedade pa, b é falsa, então dizemos que "a não está relacionado com b
mediante a R", aŔb.
Seja R uma relação e sejam os conjuntos A e B. Dizemos que R é uma relação
sobre A desde que R ⊆ A × A; e dizemos que R é uma relação de A para B se
R ⊆ A × B. Como, formalmente, uma relação é um conjunto, todas as operações sobre
conjuntos se aplicam às relações.
Exemplo:
1) Sejam os conjuntos E = 0, 1, 2, 3 e F = 4, 5, 6. São exemplos de relações:
R 1 = x, y ∈ E × F/x + y = 6
R2 = 
R 3 = 0, 4, 0, 5, 0, 6
R 4 = 2, 5, 3, 6
3
Propriedades de relação:
1) Reflexiva
Dizemos que R é reflexiva quando todo elemento de A se relaciona consigo mesmo,
isto é,
∀x ∈ A, vale xRx
Exemplos:
Considerando A = a, b, c e R uma relação sobre A.
a) R = a, a, b, b, c, c, a, b, b, c é reflexiva.
b) R = a, a, a, b, b, a, b, b, b, c não é reflexiva.
2) Simétrica
Dizemos que R é simétrica se vale yRx sempre que vale xRy, isto é,
∀x, y ∈ A, se xRy, então yRx.
Contrapositiva:
Exemplos:
Considerando A = a, b, c e R uma relação sobre A.
a) R = a, a, a, b, b, a, c, c é simétrica.
b) R = a, a, a, b, b, b, b, c não é simétrica.
3) Transitiva.
Dizemos que R é transitiva se vale xRz sempre que vale xRy e yRz, isto é,
∀x, y, z ∈ A, se xRy e yRz, então xRz.
Contrapositiva:
Exemplos:
Considerando A = a, b, c e R uma relação sobre A.
a) R = a, b, b, b, b, c, a, c, c, c é transitiva.
b) R = a, b, a, a, b, c, c, c não é transitiva.
4) Anti-simétrica.
Dizemos que R é anti-simétrica se vale x = y sempre que vale xRy e yRx, isto é,
∀x, y ∈ A, se xRy e yRx, então x = y.
Contrapositiva:
Exemplos:
Considerando A = a, b, c e R uma relação sobre A.
a) R = a, a, a, b, b, c, c, a é anti-simétrica.
b) R = a, a, b, b, c, c, b, c, c, b não é anti-simétrica.
Considerando A uma família de conjuntos e seja R a relação em A definida por "X é
um subconjunto de Y". R é anti-simétrica.
4
Definição 5: Uma relação R sobre um conjunto A ≠  é chamada de relação de
equivalência sobre A se, e somente se, R é reflexiva, simétrica e transitiva. Ou seja, R
deve cumprir, respectivamente, as seguintes propriedades:
1) Se x ∈ A, xRx
2) Se x, y ∈ A e xRy, então yRx.
3) Se x, y, z ∈ A e xRy e yRz, então xRz.
Exemplos: São relações de equivalência:
1) A = a, b, c com R = a, a, b, b, c, c, a, b, b, a.
2) A = a, b, c com R = a, a, b, b, c, c, a, b, b, a, a, c, c, a.
Contra-exemplo: Não é uma relação de equivalência:
A = ℤ com R = x, y ∈ ℤ 2 /mdcx, y = 1.
Definição 6: Seja R uma relação de equivalência sobre A. Dado a ∈ A. Chama-se
classe de equivalência determinada por a, módulo R, o subconjunto a ∈ A constituído
pelos elementos x tais que xRa.
a = x ∈ A/xRa
Exemplos:
1) R = a, a, b, b, c, c, a, b, b, a de A = a, b, c. R é uma relação de
equivalência de A.
São classes de equivalência: a = a, b, b = a, b, c = c.
Definição 7: O conjunto das classes de equivalência módulo R será indicado por E|R
e chamado conjunto-quociente de E por R.
Exemplos
1) R = a, a, b, b, c, c, a, b, b, a de E = a, b, c. R é uma relação de
equivalência de E.
E|R = a, b, c
Definição 8: Uma relação R sobre um conjunto A ≠  é chamada de relação de
ordem parcial sobre A se, e somente, se R é reflexiva, antissimétrica e transitiva. Ou
seja, R deve cumprir respectivamente as seguintes propriedades:
1) Se x ∈ A, xRx
2) Se x, y ∈ A e xRy e yRx, então x = y.
3) Se x, y, z ∈ A e xRy e yRz, então xRz.
5
Como R é uma relação de ordem parcial sobre A, para exprimir que a, b ∈ R,
usaremos a notação a ≤ bR, que se lê "a precede b na relação R" ou "b segue a na
relação R". Para exprimir que a, b ∈ R e a ≠ b, usaremos a notação a < bR, que se lê
"a precede estritamente b na relação R" ou "b segue estritamente a na relação R".
Outra notação que se poderá usar para exprimir que "a precede b " é a ≤ b. Mas isso
pressupõe o entendimento de que, nesse caso, "≤" não significa necessariamente
"menor ou igual a", no sentido numérico usual. O sentido é aquele definido pelo
contexto da questão em foco. Analogamente, a notação "a < b" poderá ser usada para
exprimir que "a precede estritamente b", com um sentido que não o usual.
Exemplos:
1) A relação R = a, a, b, b, c, c, a, b, b, c, a, c é uma relação de ordem sobre
E = a, b, c.
2) A relação R sobre ℤ definida por xRy se, somente se, x ≤ y (≤: "menor ou igual a")
é uma relação de ordem, denominada ordem usual, pois:
i) Reflexiva: Para todo x ∈ ℤ, tem-se que x ≤ x.
ii) Anti-simétrica: Dados x, y ∈ ℤ, se x ≤ y e y ≤ x, então x = y.
iii) Transitiva:Dados x, y, z ∈ ℤ, se x ≤ y e y ≤ z, então x ≤ y.
3) A relação de inclusão sobre o conjunto das partes PE de um dado conjunto E é
uma relação de ordem.
Contra-exemplo:
1) A relação R sobre ℤ definida por xRy se, somente se, x < y não é uma relação de
ordem e nem de equivalência.
Enunciaremos a seguir os axiomas referentes à relação "menor ou igual".
Propriedades:
i) Tricotomia: Dados a, b ∈ ℤ, tem-se que ou a < b ou a = b ou b < a. (Aqui a < b
significa que a ≤ b, com a ≠ b.
ii) Dados a, b, c ∈ ℤ, se a ≤ b, então a + c ≤ a + c.
ii) Dados a, b, c ∈ ℤ, se a ≤ b e 0 ≤ c, então αc ≤ bc.
Proposição 6:
Seja a um inteiro. Então
i) Se a ≤ 0, então 0 ≤ −a.
ii) Se 0 ≤ a, então −a ≤ 0.
iii) 0 ≤ a 2 (isto é, todo quadrado é não negativo).
iv) 0 < 1.
6
Definição 9: Um conjunto parcialmente ordenado é um conjunto sobre o qual se
definiu uma certa relação de ordem parcial.
Definição 10: Seja R uma relação de ordem parcial sobre A. Os elementos a, b ∈ A
se dizem comparáveis mediante R se a ≤ b ou b ≤ a.
Definição 11: Se dois elementos quaisquer de A forem comparáveis mediante R,
então R será chamada relação de ordem total sobre A. Nesse caso, o conjunto A é
dito conjunto totalmente ordendado por R.
Exemplos:
1) A relação R = a, a, b, b, c, c, a, b, b, c, a, c é uma relação de ordem sobre
E = a, b, c. E é um conjunto totalmente ordenado por R.
2) A relação R sobre ℤ definida por xRy se, somente se, x ≤ y (≤: "menor ou igual a")
é uma relação de ordem, denominada ordem usual.
Podemos dizer que ℤ é um conjunto totalmente ordenado pela relação de ordem
usual.
3) A relação de inclusão sobre o conjunto das partes PE de um dado conjunto E é
uma relação de ordem. Então PE não é um conjunto totalmente ordenado pela relação
de inclusão.
4) A relação R sobre ℕ definida por:
xRy se e, somente se, x é divisor de y.
é uma relação de ordem. Mas o conjunto ℕ é parcialmente ordenado por essa
relação. Essa ordem não ordena totalmente ℕ porque há elementos de ℕ não
comparáveis por divisibilidade, como, por exemplo o 2 e 3. 2 não é divisor de 3 e 3 não é
divisor de 2.
Representação gráfica simplicada.
Para representar uma relação de ordem sobre um conjunto finito E, podemos utilizar
um esquema simplicado que substitui o esquema de flechas já visto. É assim:
1º) quando aRb, ligamos o elemento a ao elemento b por meio de um traço
ascendente;
2º) deixamos de desenhar os laços em torno de cada elemento de E (não expomos
a propriedade reflexiva);
3º) quanto existe um traço ligando a com b e um outro traço ligando b com c,
deixamos de desenhar um traço ligando a com c (não expomos a propriedade
transitiva).
Exemplos:
1) E = 1, 2, 3, 4, 6, 12. R é ordem habitual ≤.
2) E = 1, 2, 3, 4, 6, 12. S é a ordem por divisibilidade.
7
Definição 12: Seja E um conjunto parcialmente ordenado mediante a relação ≤. Seja
A um subconjunto de E, com A ≠ . Diz-se que um subconjunto A de números inteiros é
limitado à direita ou limitado superiormente se existe um número d tal que a ≤ d para
todo a ∈ A.
Diz-se que um subconjunto A de números inteiros é limitado à esquerda ou limitado
inferiormente se existe um número c tal que c ≤ a para todo a ∈ A.
Definição 13: Um número d ∈ A é o elemento máximo do conjunto A quando a ≤ d
para todo a ∈ A. Um número c ∈ A é o elemento mínimo do conjunto A quando c ≤ a
para todo a ∈ A.
Notação: maxA = d
minA = c
Exemplos:
1) Se E = ℤ, A = x ∈ ℤ/0 < x ≤ 10 e a ordem é a habitual.
2) Se E = 1, 2, 3, 4, 6, 9, 12, 18, 36, A = 2, 4, 6 e a ordem é a divisibilidade.
Princípio da Boa Ordem: Todo conjunto não-vazio de inteiros não-negativos
contém um elemento mínimo.
Proposição 7: Não existe a ∈ ℤ + tal que 0 < a < 1.
Proposição 8 (Propriedade Arquimediana): Sejam a e b inteiros positivos. Então,
existe um inteiro positivo n tal que na > b.
Proposição 9: Todo conjunto não-vazio de inteiros limitados inferiormente tem
mínimo.
8
Exercícios
1. Sejam a, b inteiros. Mostrar que:
a) −1a = −a
b) Se a 2 = 0, então a = 0.
c) Se a 2 = a, então a = 0 ou a = 1.
2. Prove que a subtração não é comutativa nem associativa,mas é válida a
distributiva da multiplicação em relação à subtração.
3. Demonstre que para todos a, b, c ∈ ℤ :
a) ab − c = ab − ac
b) −a + −b = −a + b
4. Sejam a, b ∈ ℤ, tais que a < b. Provar que −a > −b.
5. Mostre que para todos a, b ∈ ℤ, a < b ⇔ a − b < 0.
6. Prove que para todos a, b ∈ ℤ,
a) −|a| ≤ a ≤ |a|
b) |a| − |b| ≤ |a + b|
c) |a| − |b| ≤ |a − b|
d) |a + b| ≤ |a| + |b|
e) |a − b| ≤ |a| + |b|
f) |a. b| = |a|. |b|
7. Mostre que se a e b são números inteiros tais que a. b = 1, então a e b são ambos
iguais a 1 ou a −1.
8. Para cada uma das seguintes relações definidas no conjunto A = 1, 2, 3, 4, 5,
determine se a relação é reflexiva, anti-simétrica e/ou transitiva.
a) R = 1, 1, 2, 2, 3, 3, 4, 4, 5, 5
b) R = 1, 2, 2, 3, 3, 4, 4, 5
c) R = 1, 1, 1, 2, 1, 3, 1, 4, 1, 5
d) R = 1, 1, 1, 2, 2, 1, 3, 4, 4, 3
e) R = 1, 2, 3, 4, 5 × 1, 2, 3, 4, 5
9. Digamos que dois inteiros estão próximos um do outro se sua diferença for no
máximo 2 (isto é, os números estão a uma distância de no máximo 2). Por exemplo, 3
9
está próximos de 5, 10 está próximo de 9, mas 8 não está próximo de 4. Representemos
por R está relação estar próximo de.
a) Escreva R como um conjunto de pares ordenados. Sua resposta deve
apresentar-se como segue:
R = x, y/
Prove ou refute:
b) R é reflexiva
c) R é simétrica
d) R é anti-simétrica
e) R é transitiva
10. Seja R uma relação tem o mesmo tamanho que definida sobre todos os
subconjuntos finitos de ℤ (isto é, ARB se e somente se |A| = |B|). Quais das 4
propriedades (reflexiva, simétrica, anti-simétrica e transitiva) R possui? Prove suas
respostas.
11. Quais dos seguintes conjuntos são relações de equivalência?
a) R = 1, 1, 1, 2, 2, 1, 2, 2, 3, 3 no conjunto 1, 2, 3.
b) R = 1, 2, 2, 3, 3, 1 no conjunto 1, 2, 3.
c) ≤ em ℤ.
d) 1, 2, 3 × 1, 2, 3 no conjunto 1, 2, 3.
e) 1, 2, 3 × 1, 2, 3 no conjunto 1, 2, 3, 4.
12. Para cada relação de equivalência, ache a classe de equivalência pedida.
a) R = 1, 1, 1, 2, 2, 1, 2, 2, 3, 3, 4, 4 no conjunto 1, 2, 3, 4. Ache 1 .
b) R = 1, 1, 1, 2, 2, 1, 2, 2, 3, 3, 4, 4 no conjunto 1, 2, 3, 4. Ache 4 .
c) R é tem-os-mesmos-pais-que no conjunto de todos os seres humanos. Ache você.
d) R é tem-a-mesma-data–de-aniversário-que no conjunto de todos os seres
humanos. Ache você.
13) Há apenas uma relação de equivalência possível em um conjunto de um
elemento: se A = 1, então R = 1, 1 é a única relação de equivalência possível. Há
exatamente duas relações de equivalência possíveis em um conjunto de dois
elementos: A = 1, 2, então R 1 = 1, 1, 2, 2 e R 2 = 1, 1, 1, 2, 2, 1, 2, 2 são as
únicas relações equivalência em A. Quantas relações de equivalência diferentes são
possíveis em um conjunto de três elementos? Em um conjunto de quatro elementos?
Exercícios 14 a 17 estão em outra folha.
18) Faça o diagrama simplicado das seguintes ordens no conjunto
E = 1, 2, 4, 5, 10, 20 :
a) ordem habitual
10
b) ordem por divisibilidade.
19) Faça o diagrama simplicado da relação de ordem por inclusão em E = Pa, b.
20) Faça o diagrama simplicado da relação de ordem por divisibilidade no conjunto
E = 2, 3, 5, 6, 10, 15, 30.
21) Faça o diagrama simplicado da relação de ordem por inclusão no conjunto
E=a, b, a, b, c, a, b, d, a, b, c, d, a, b, c, d, e.
11