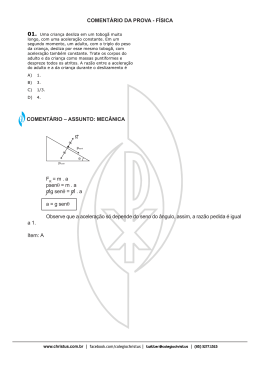
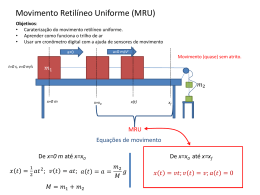
Universidade Estadual de Mato Grosso do Sul
Curso de Física - Laboratório de Física Experimental A
1
Prof. Paulo César de Souza
ROTEIRO DA EXPERIÊNCIA Nº 6 (‫)ו‬
MOVIMENTO RETILÍNEO UNIFORME VARIADO (MRUV)
1 Objetivos
Observação e caracterização do movimento retilíneo uniformemente acelerado
(MRUV) sob a influência de um campo gravitacional num plano inclinado.
2 Introdução
Na Figura 1 apresentamos um corpo massa m , submetido a uma força gravitacional
P , num plano inclinado de angulação θ.
m num plano inclinado com ângulo θ. A atuação de uma
força gravitacional P e suas componentes são mostradas.
Figura 1 Esquema de um corpo de massa
Pela 2ª lei de Newton1 a força resultante F que atua sobre um corpo com massa m
e aceleração a será:
dp
dv
F=
= m⋅a = m⋅
(1)
dt
dt
p é o momento e v a velocidade instantânea. No caso do plano inclinado a aceleração
será a = g ⋅ senθ , assim a equação (1) aplicada ao problema resultará em:
dv
(2)
m ⋅ g ⋅ senθ = m ⋅
dt
A solução da equação (2) para a velocidade ( v ) e a posição ( s ) será:
2
v ( t ) = v0 + g ⋅ senθ ⋅ t
(3)
g ⋅ senθ 2
s ( t ) = s0 + v0 ⋅ t +
⋅t
2
A posição inicial e velocidade inicial são s0 e v0 , respectivamente. No caso do corpo partir
do repouso tem-se:
s ( t ) = 12 g ⋅ senθ ⋅ t 2
(4)
3 Esquema e Procedimento Experimental
Nessa experiência utilizaremos o arranjo experimental mostrado na Figura 2. O
corpo de prova é um carrinho presente num plano inclinado de 5º que desliza praticamente
sem atrito sobre um colchão de ar. O funcionamento do dispositivo é relativamente
simples: após a passagem do carrinho pelo primeiro sensor o cronômetro digital começa a
contagem do tempo de passagem entre cada sensor seqüente. Um gerador de fluxo de ar
acoplado a régua metálica cria o colchão de ar que faz o carrinho deslizar quase sem
atrito.
Figura 2 Arranjo experimental do movimento retilíneo uniforme. A régua metálica possui cinco
fotossensores, ligados a um cronômetro digital, e um gerador de fluxo (não mostrado) de ar
que permite o carrinho percorrer o trajeto praticamente sem atrito. O carrinho possui uma
haste que ao passar pelos fotossensores aciona o cronômetro digital.
É aconselhável ao experimentador a escolha de cinco posições diferentes para a
fixação dos sensores na régua metálica do sistema, a Figura 2 apresenta uma sugestão.
Antes do lançamento a haste do carrinho deve estar o mais próximo possível do primeiro
fotossensor para que a equação (4) seja válida. O experimentador deve realizar no mínimo
5 lançamentos distintos partindo sempre do mesmo ponto.
3
4 Análise dos Resultados e Apresentação
(a) Elabore uma tabela com os valores de ∆S (espaços), ∆t (intervalos de tempo) e
v (velocidades média). Determine a incerteza experimental de cada grandeza física
medida.
(b) Faça um gráfico em papel milimetrado dos valores medidos S x t 2 (com barras de
incertezas transferidas) e aplicando os mínimos quadrados2 determine g ⋅ senθ e a
aceleração da gravidade local com as respectivas incertezas. Compare com o valor
para Dourados-MS – justifique seus resultados.
(c) Para verificar o modelo da dependência quadrática3 com o tempo utilize um papel
dilog fazendo o gráfico S x t (com barras de incerteza). Determine os coeficientes
graficamente.
5 Discussão dos resultados
O experimentador deve reunir indícios experimentais para elaborar uma discussão
madura dos resultados e suas conclusões. Os itens a seguir devem ser respondidos:
I. Os parâmetros iniciais que caracterizam o movimento do corpo de prova são
razoáveis para a escolha do modelo apresentado na equação (4)?
II. O valor encontrado da aceleração da gravidade está de acordo com os valores
encontrado pelo pêndulo simples e queda-livre? E os valores tabelados para
Dourados-MS?
III. Se o corpo tivesse outra forma como seriam os resultados?
6 Referências
1
H.M. Nussenzveig, Curso de Física Básica 1 - Mecânica, Editora Edgard Blücher Ltda, 3ª
ed., São Paulo (1996).
2
J. H. Vuolo, Fundamentos da Teoria de Erros, Editora Edgard Blücher Ltda., São Paulo,
1992.
3
http://www2.uefs.br/depfis/sitientibus/vol1/Alvaro_Main-SPSS.pdf